[프로그래머스] Lv2. 당구 연습 - JavaScript

문제분류 : 코팅테스트 연습

난이도 : Level 2

출처 : 프로그래머스 - 당구 연습

문제

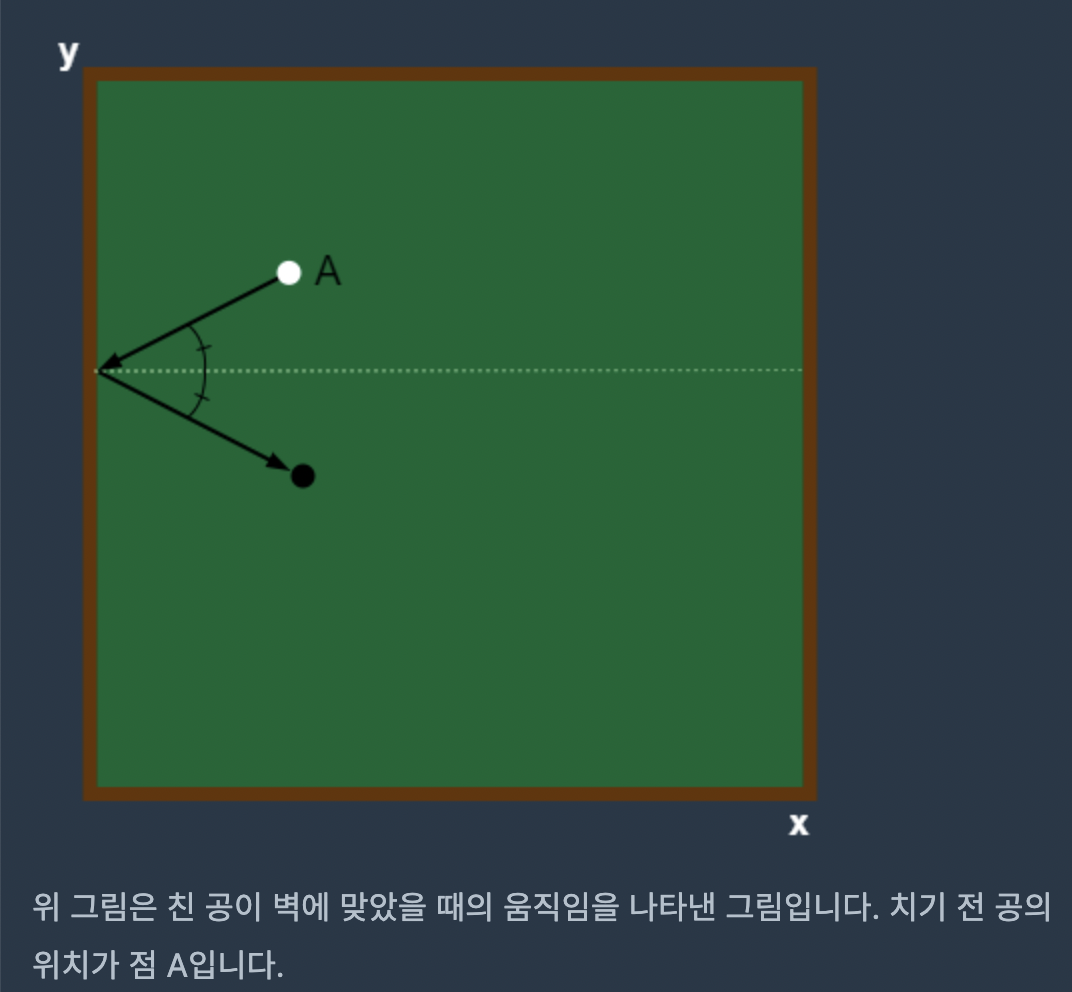
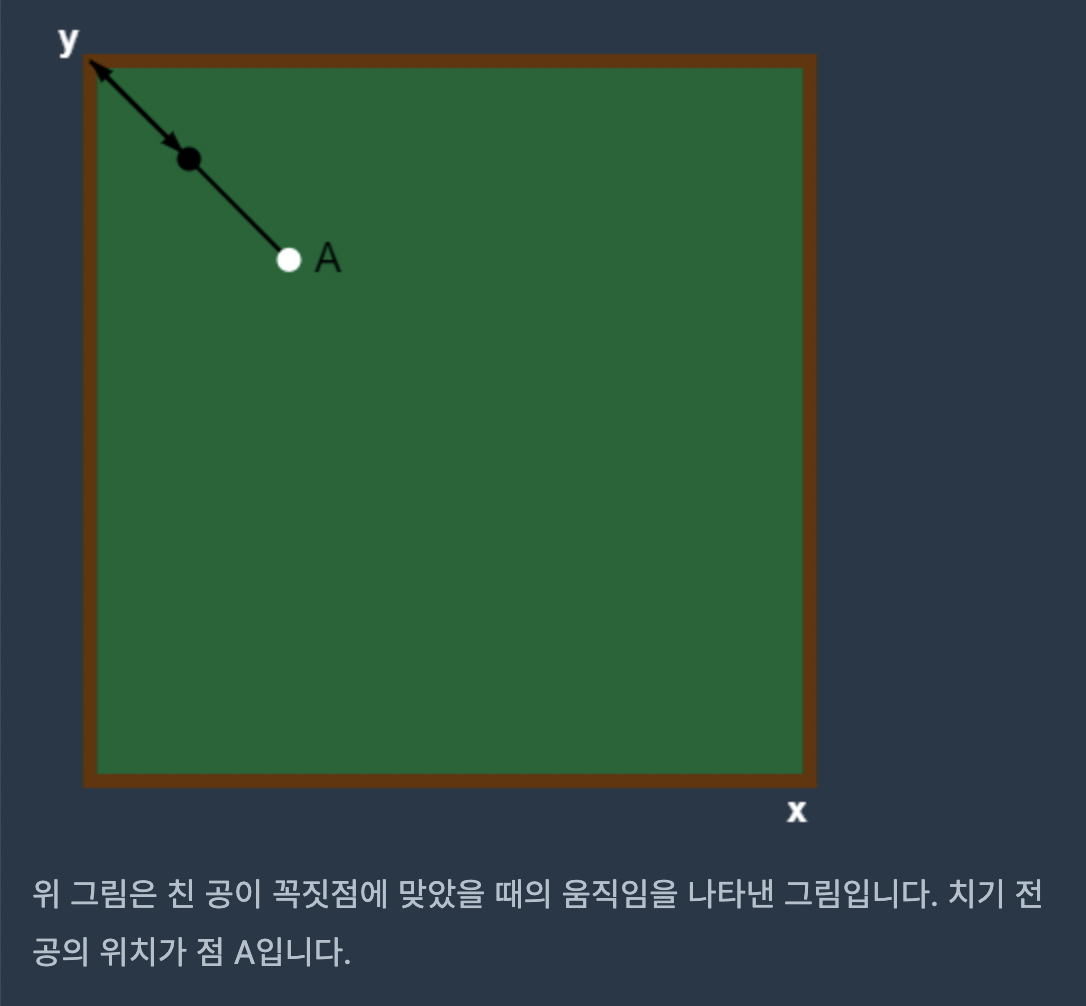
제한사항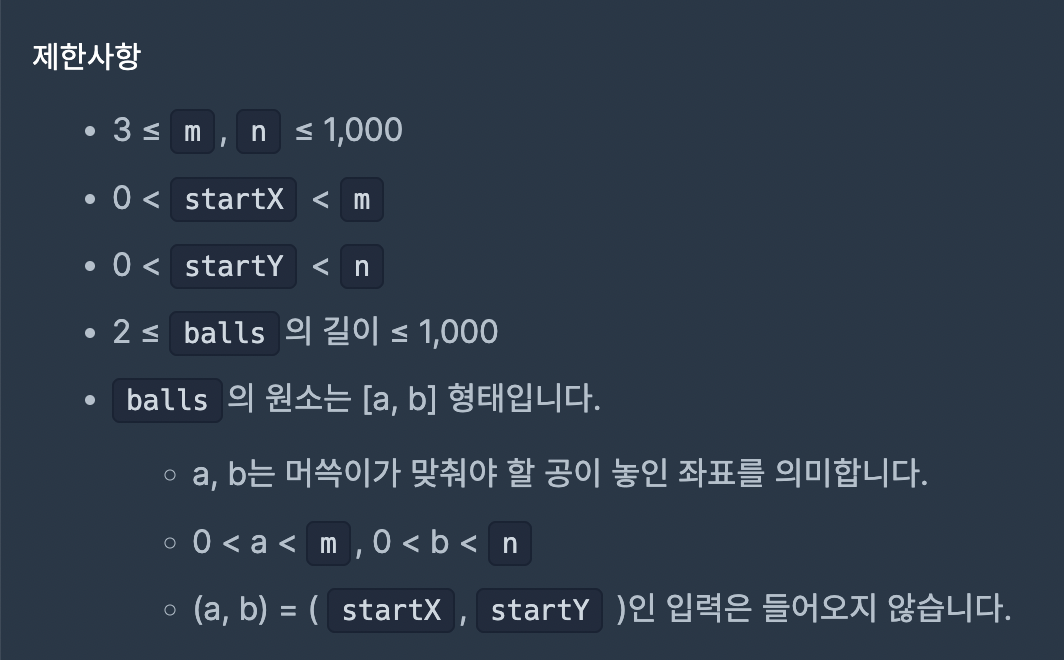

📌 내가 생각한 풀이

완전 구현문제이다. 최단경로는 대칭이동을 이용하면 되므로, 문제를 잘 읽고 경우의 수를 나누고 대칭이동을 이용하여 문제를 풀자.

1. x좌표가 같을때
   1-1 시작공의 y좌표가 맞추는공의 y좌표보다 클때
   1-2 시작공의 y좌표가 맞추는공의 y좌표보다 작을때
2. y좌표가 같을때
   2-1 시작공의 x좌표가 맞추는공의 x좌표보다 클때
   2-2 시작공의 x좌표가 맞추는공의 x좌표보다 작을때
3. x좌표, y좌표가 다를때

function solution(m, n, startX, startY, balls) {
    var answer = [];
    balls.map((data,idx)=>{
        let x = m;
        let y = n;
        let start = [startX, startY];
        let goal = data
        if(start[0] === goal[0]){
            //x좌표가 같을때
            let arr = [];
            //case 1 -> 오른쪽으로 팅구기
            let num = start[0] + (m-start[0])*2
            let sum = Math.pow(goal[0]-num,2) + Math.pow(start[1]-goal[1],2);
            arr.push(sum);
            //case 2 -> 왼쪽으로 팅구기
            num = start[0] * -1;
            sum = Math.pow(goal[0]-num,2) + Math.pow(start[1]-goal[1],2);
            arr.push(sum);
            if(start[1] > goal[1]){
                //case 3 -> 아래쪽 이동 불가, 위쪽 쿠션만 가능
                num = start[1] + (n-start[1])*2
                arr.push(Math.pow(num-goal[1],2))
            }else{
                //case 3 -> 위쪽 이동 불가, 아래쪽 쿠션만 가능
                num = start[1] * -1;
                arr.push(Math.pow(num-goal[1],2))
            }
            answer.push(Math.min(...arr));
        }else if(start[1] === goal[1]){
            //y좌표가 같을때
            let arr = [];
            //case 1 -> 위로 팅구기
            let num = start[1] + (n-start[1])*2
            let sum = Math.pow(goal[0]-start[0],2) + Math.pow(num-goal[1],2);
            arr.push(sum);
            //case 2 -> 아래로 팅구기
            num = start[1] * -1;
            sum = Math.pow(goal[0]-start[0],2) + Math.pow(num-goal[1],2);
            arr.push(sum);
            if(start[0] > goal[0]){
                //case 3 -> 왼쪽 이동 불가, 오른쪽 쿠션만 가능
                num = start[0] + (m-start[0])*2
                arr.push(Math.pow(num-goal[0],2))
            }else{
                //case 3 -> 오른쪽 이동 불가, 왼쪽 쿠션만 가능
                num = start[0] * -1;
                arr.push(Math.pow(num-goal[0],2))
            }
            answer.push(Math.min(...arr));
            
        }else{
            //x좌표 y좌표가 다 다를때 모든 팅구는거 다 비교?
            let arr = [];
            //case1 -> 위로팅구기
            let num = start[1] + (n-start[1])*2
            let sum = Math.pow(goal[0]-start[0],2) + Math.pow(num-goal[1],2);
            arr.push(sum);
            //case2 -> 오른쪽으로 팅구기
            num = start[0] + (m-start[0])*2
            sum = Math.pow(goal[0]-num,2) + Math.pow(start[1]-goal[1],2);
            arr.push(sum);
            //case3 -> 왼쪽으로 팅구기
            num = start[0] * -1;
            sum = Math.pow(goal[0]-num,2) + Math.pow(start[1]-goal[1],2);
            arr.push(sum);
            //case4 ->아래로 팅구기
            num = start[1] * -1;
            sum = Math.pow(goal[0]-start[0],2) + Math.pow(num-goal[1],2);
            arr.push(sum);
            answer.push(Math.min(...arr))
        }
    })
    return (answer)
    
}

📌 느낀점

비교적 단순한 구현문제였다. 처음엔 최단경로라 해서 dp나 그래프탐색을 생각하였지만, 단순한 대칭이동을 이용하여 최솟값을 찾는 문제였다. 하지만 경우의 수가 많으므로 세분화하여 잘 나누어서 풀어야했다.