(작성중) [논문 리딩] Attention Is All You Need

최지원·2023년 5월 20일

논문 리딩

목록 보기

1/2

⌜Attention Is All You Need⌟는 transformer에 관한 논문이다.

transformer가 등장하기 이전의 sequence transduction model들은 RNN, LSTM, GRU 등 순환신경망에 의존하고 있었다. 이러한 sequence model은 근본적으로 time step에 따라 계산을 진행하는 순차적 특성을 갖고 있는데, 이러한 특성이 병렬화(parallelization)을 방해한다.

예를 들어서, seq2seq model(with RNN)에서 "I am a student"라는 문장의 self attentnion을 계산하려면, 우선 'I'와 'I', 'am', 'a', 'student'와의 attention을 각각 계산해야한다. 그리고 다음 time step에 'am'과 'I', 'am', 'a', 'student'와의 attention을 계산한다. 이러한 순차적 특성이 병렬화를 불가능하게 한다.

이러한 단점을 극복하기 위해서 제안된 transformer는 순환신경망을 사용하지 않고 전적으로 attention 메커니즘에 의존한 모델이다.
transformer는 병렬적 처리가 가능하기 때문에 GPU를 사용하면 매우 빠른 성능을 보여준다.

3. Model Architecture

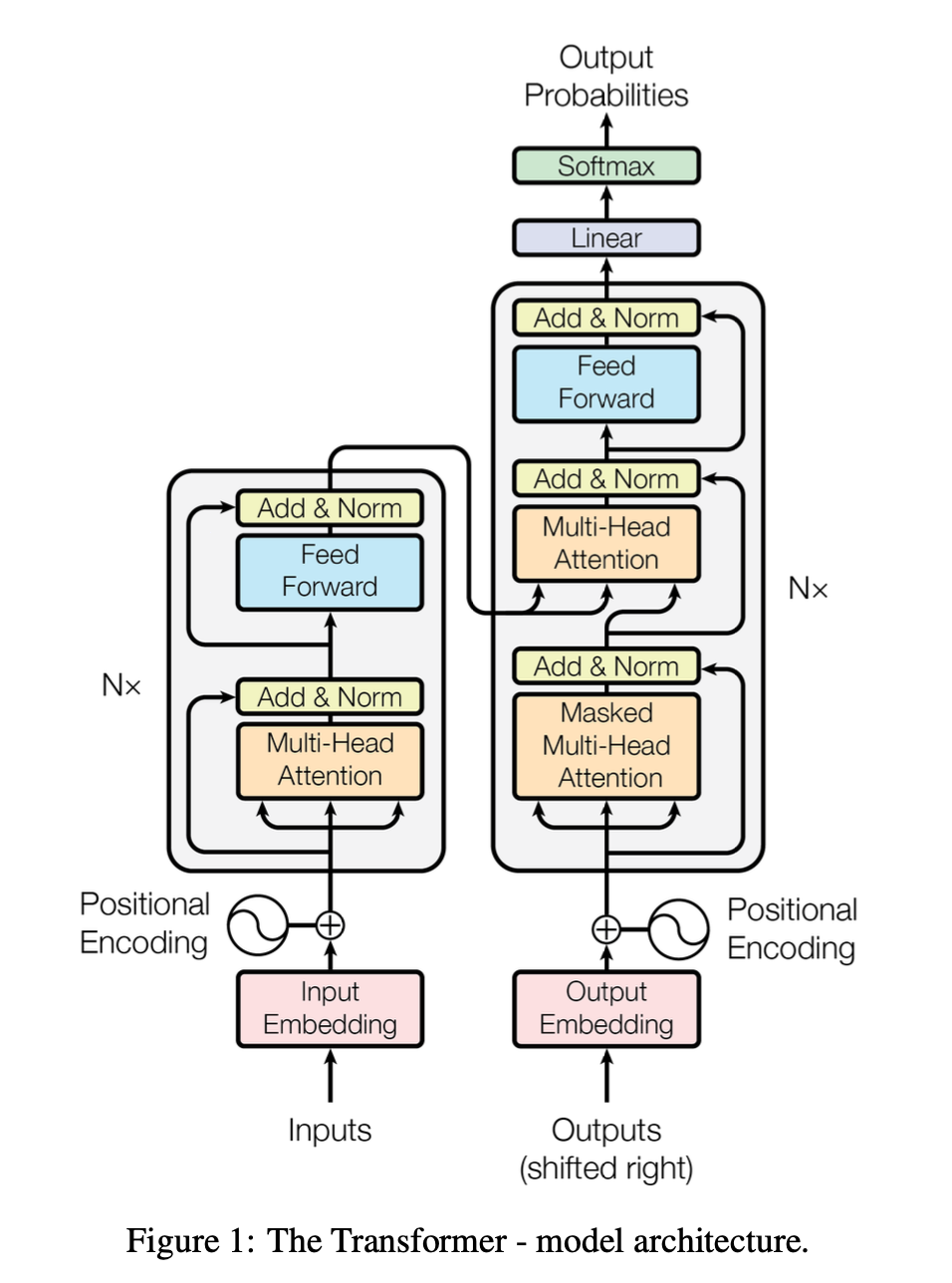
3.1 Encoder and Decoder Stacks

Encoder

Encoder는 동일한 layer를 쌓아 만든다. 논문에서는 N=6만큼의 layer를 쌓아 만들었다. 각 layer는 두 개의 sub-layer로 구성된다.

첫 번째는 Multi-Head (Self) Attention, 두 번째는 (position-wise fully connected) Feed Forward Network이다.

그리고 각 sublayer에는 normalization으로 연결되는 residual connection이 존재한다. residual connection은 gradient vanishing 문제를 완화하고 깊은 신경망이 원활하게 학습할 수 있도록 해준다. 각 sub-layer의 output을 나타내면 아래와 같다.

LayerNorm(x+Sublayer(x))

그리고 논문에서는 이러한 residual connection을 용이하게 하기 위해서 $d_{model}=512$ 로 설정했다. ~~이유는 잘 모르겠다~~

Decoder

Decoder도 동일한 N=6만큼의 layer를 쌓아 만든다. 추가적으로 Decoder의 각 layer에는 sub-layer 하나가 더 존재한다. 이 sub-layer는 Encoder의 output에 Multi-Head Attention을 수행하는 역할로, Multi-Head Attention layer이다.

🚨 주의
Decoder의 Masked Multi-Head Attention은 Encoder의 Multi-Head Attention과 매치된다. 따라서 Decoder의 Multi-Head Attention을 새로 추가 된 sub-layer로 보는 것이 타당하다. 화살표의 방향만 봐도 금방 이해할 수 있다.

그렇다면 Decoder의 Masked Multi-Head Attention은 무엇이고, 왜 Masking을 할까?

Decoder의 Masked Multi-Head Attention은 Encoder의 Multi-Head Attention과 비슷하게 자기 자신과 Self Attention을 수행하는 sub-layer이다.

차이점은 Decoder 자신이 생성한 output을 다음 time step의 input으로 사용한다는 점이다. 그림을 보면 Output Embedding이 input으로 들어가는 것을 확인할 수 있다. Masking을 하는 이유도 여기서 찾을 수 있다.

모델을 훈련시킬 때, Decoder에서 결과값(output) 전체를 참조해 output을 생성하도록 훈련시킨다면, 문제가 생긴다. 모델을 테스트할 때는 output 전체가 주어지는 것 아니라 timestep에 따라 순차적으로 output을 하나씩 생성해야 하는데, 모델을 훈련시킬 때 순차적 참조가 아닌 output 전체를 참조하도록 하였으므로 성능에 이상이 생길 수 있는 것이다.

따라서 모델의 훈련 과정에서도 순차적 예측 성능을 강제하기 위해서, 미래의 output값을 참조하지 못하도록 masking을 한다.

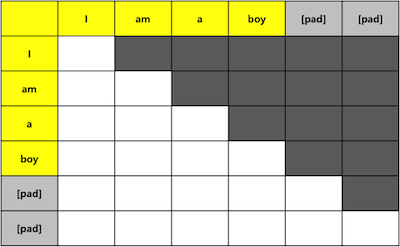
또한 Encoder와 동일하게 residual connection과 normalization을 적용시킨다.

3.2 Attention

3.2.1 Scaled Dot-Product Attention

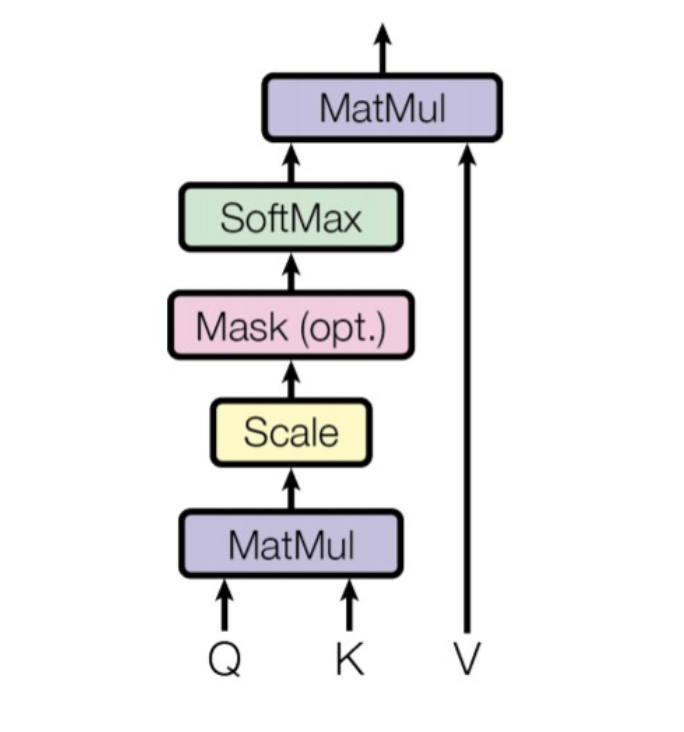
Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V

Query-Key set과 Value가 matrix로 주어질 때 Attention은 위와 같이 계산한다. 여기서 일반적인 dot-product attention과 다르게 $\frac{1}{\sqrt{d_k}}$ 를 scaling하는 이유는 무엇일까?

attention을 계산하는 방법은 크게 두 가지로 나뉜다.

additive attention
dot-product attention

이론적으로 두 방식의 복잡도는 비슷하지만, 실제로는 dot-product attention이 더 빠르고 메모리 공간 사용량도 적다. 왜냐하면 matrix multiplication 코드가 엄청나게 최적화되어 있기 때문이다. 이 논문에서도 기본적으로 dot-product attention 방식을 사용했다.

하지만 일반적으로 $d_k$ (dimension of key)가 커질 수록 dot-product attention의 성능이 떨어진다. 그 이유를 살펴보자.

$d_k$ 가 커질 수록 dot product의 결과값( $QK^T$ )이 커진다. $QK^T$ 는 다시 softmax의 입력값으로 사용된다. 여기서 softmax의 입력값들의 scale이 커지기 때문에, softmax의 출력값들의 편차가 커져, gradient vanishing 문제가 발생한다.
(softmax는 지수함수를 사용하여 출력값을 계산하기 때문에 입력값의 크기가 커질 수록 출력값의 편차는 커진다.)

그래서 $d_k$ 가 커질 수록 dot-product attention의 성능이 저하되는 것이다. 이 논문에서는 $\frac{1}{\sqrt{d_k}}$ 를 scaling factor로 사용하여 gradient vanishing 문제를 완화했다. 그리고 이 방식을 scaled dot-product라고 명명한다.

3.2.2 Multi-Head Attention

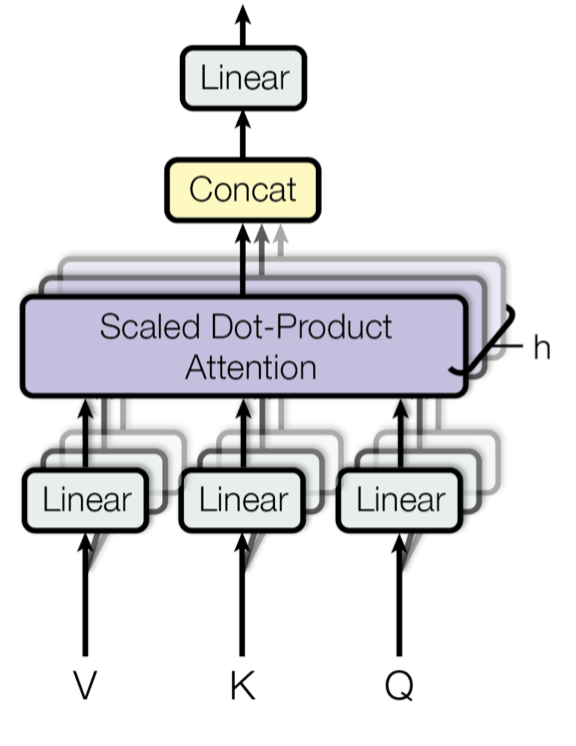
논문의 연구진들은 하나의 query, key, value set에 attention을 수행하는 것보다 h개의 다른 query, key, value set에 attention을 수행하는 것이 더 효과적이다는 것을 발견했다. 전자를 (single-head) attention, 후자를 multi-head attention이라고 한다.

MultiHead(Q,K,V)=Concat(head_1, ..., head_h)W^O

where\ head_i=Attention(QW_i^Q,KW_i^K,VW_i^V)

여기서 Q, K, V는 모두 embedding된 input matrix X가 복사된 것이다. ~~아무리 봐도 X인 것 같은데 Q, K, V로 구분해서 써놓아서 다른 의미가 있는지 엄청 헤맸다.~~ 다시 말해서 Q = K = V = X 이다.

그리고 직접 matrix의 shape(dimension)이 어떻게 변하는지 따져 보면 multi-head attention을 이해하는데 도움이 된다.

W_i^Q∈ℝ^{d_{model}✕d_k}, W_i^K∈ℝ^{d_{model}✕d_k}, W_i^V∈ℝ^{d_{model}✕d_v}, W^O∈ℝ^{hd_v✕d_{model}}

$d_{model}$ 은 각 단어의 embedding 차원, $d_k$ 는 query와 key의 차원, $d_v$ 는 value의 차원이다. 여기서 query와 key의 차원이 같은 이유는 attention을 계산할 때 $QK^T$ matrix multiplication을 해야하기 때문이다. $h$ 는 attention을 분할하는 head의 개수이다.

"I am a student."라는 문장의 multi-head self attention 과정을 따라가보자.

우선, 각 단어는 embedded vector로 나타낼 수 있고, vector들을 합쳐서 matrix X로 나타낼 수 있다. 이 때 X의 shape은 아래와 같다.

$X.shape=(seq\_len,d_{model})$

이제 X의 query, key, value matrix를 구해야한다. 이는 X와 각 weight matrix를 dot-product해서 구할 수 있다. 각 weight matrix의 shape과 query, key, value matrix의 shape은 아래와 같다.

$W^Q.shape=(d_{model},d_k,h)\ \ \ \ \ \ \ \ \ \ Q=XW^Q.shape=(seq\_len,d_k,h)$
$W^K.shape=(d_{model},d_k,h)\ \ \ \ \ \ \ \ \ \ K=XW^K.shape=(seq\_len,d_k,h)$
$W^V.shape=(d_{model},d_v,h)\ \ \ \ \ \ \ \ \ \ V=XW^V.shape=(seq\_len,d_v,h)$

single-head attention이라면 2-dimensional matrix였겠지만, multi-head attention이기 때문에 head 수 만큼 matrix를 stack해서 3-dimensional matrix를 만들어준다.

이제 준비가 끝났으니 진짜 Attention을 구하기 위해서 $softmax(\frac{QK^T}{\sqrt{d_k}})V$ 의 shape를 계산해보자. 여기서 scaling과 softmax함수는 shape에 영향을 미치지 않으므로 $softmax(\frac{QK^T}{\sqrt{d_k}})$ 의 shape은 $QK^T$ 의 shape과 같다.

$softmax(\frac{QK^T}{\sqrt{d_k}}).shape=QK^T.shape=(seq\_len,seq\_len,h)$

$softmax(\frac{QK^T}{\sqrt{d_k}})V.shape=(seq\_len,d_v,h)$

이제 각 head의 attention을 모두 계산했으니 concatenate하고 $W^O$ 를 곱해줘야한다. 여기서 각 head의 attention을 concatenate하는 과정은 (seq_len, d_v, h)의 matrix를 2차원으로 펼치는 것과 같다.

$Concat(head_1, ..., head_h).shape=(seq\_len,hd_v)$

$W^O.shape=(hd_v,d_{model})$

$MultiHead.shape=Concat(head_1, ..., head_h)W^O.shape=(seq\_len,hd_v)$

여기서 W^O matrix의 2번째 차원은 설정하기 나름이지만, embedding된 matrix X와 shape을 갖게 하기 위해서 W^O matrix의 2번째 차원은 d_model로 설정한다.

3.2.3 Applications of Attention in our Model

self-attention in encoder
encoder의 self-attention layer에서 모든 query, key, value는 이전 encoder layer의 output에서 온다. 그러므로 encoder 내부에서 각 position은 encoder 이내의 다른 모든 position을 참조할 수 있다.

self-attention in decoder
decoder의 self-attention layer에서 모든 query, key, value는 이전 decoder layer의 output에서 온다. 하지만 auto-regressive property를 보존하기 위해서 현재 위치 이후의 정보는 사용하지 않아야 한다. auto-regressive property는 디코더가 이전에 생성한 토큰을 입력으로 사용하여 다음 토큰을 예측하는 능력을 의미한다. 이는 scaled dot-product attention을 계산할 때 softmax 일부의 input값을 -∞으로 masking함으로써 구현된다.

encoder-decoder attention (in decoder)
decoder의 encoder-decoder attention layer에서 query는 이전 decoder layer에서, key와 value는 encoder의 output에서 온다. 그러므로 decoder의 모든 position은 input sequence의 모든 position을 참조할 수 있다.

3.3 Position-wise Feed-Forward Networks

Encoder와 Decoder의 각 layer에는 Feed-Forward Network가 존재한다.

FFN(x)=max(0,xW_1+b_1)W_2+b_2

수식을 살펴보면 ( 선형 변환 - ReLU - 선형 변환 ) 의 단계로 구성되어 있다.

풀네임은 Position-wise (Fully Connected) Feed-Forward Networks인데, 각 단어의 의미도 한 번 살펴보자.

Position-wise
각 위치(단어)에 대해 개별적으로 적용되고
Fully Connected
한 층의 모든 뉴런이 다음 층의 모든 뉴런과 연결된
Feed-Forward Networks
입력을 전방향으로 전파하는 네트워크

논문에서는 input과 output의 차원을 $d_{model}=512$ , inner layer(hidden layer)의 차원을 $d_{ff}=2048$ 로 설정했다. inner layer의 차원을 확장함으로써 더 추상적인 feature를 잡아낼 수 있다.

3.4 Embeddings and Softmax

논문에서는 다른 sequence transduction models처럼 단어를 벡터로 변환할 때, 학습된 임베딩(embedding) 을 사용한다. embedding layer에서는 $\sqrt{d_{model}}$ 만큼 scailing해준다. ~~이유는 잘 모르겠다.~~

그리고 Decoder의 output을 예측된 단어의 확률로 변환하기 위해서 학습된 선형 변환과 softmax를 사용한다. 또한, 논문에서는 ⌜Using the Output Embedding to Improve Language Models⌟와 유사하게 두 embedding layer와 pre-softmax linear transformation 사이에 같은 weight matrix를 사용한다. ~~아직 이해가 잘 안된다.~~

3.5 Positional Encoding

Transformer 모델은 Recurrence나 Convolution과 같이 순차적 계산이 아니라 병렬적 계산을 하기 때문에, 단어의 순서와 같은 위치 정보를 달리 파악할 방법이 없다. 따라서 직접 token들의 절대적/상대적 위치 정보를 주입해야 한다. 이렇게 위치 정보를 주입하는 encoding 방식이 Positional Encoding이다.

Positional Encoding의 차원은 $d_{model}$ 로 embedding 차원과 같다. 따라서 positional encoding vector와 embedding vector는 더할 수 있다. 이를 통해 위치 정보가 embedding vector에 주입된다.

많은 positional encoding 방법이 존재하지만, 논문에서는 아래와 같은 방법을 사용한다.

PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})

PE_{(pos,2i+1)}=sin(pos/10000^{2i/d_{model}})

$pos = position$
$i = dimension$

연구진들이 학습된 임베딩(seq2seq) 또한 positional encoding으로 사용해보았지만, 성능 상의 차이가 거의 없었다. 결국 사인파 버전의 positional encoding을 사용했다. 왜냐하면 사인파 버전이 학습했을 때 마주했던 시퀀스의 길이보다 더 긴 시퀀스의 길이까지 잘 나타낼 수 있었기 때문이다.

4. Why Self-Attention

최지원

다음 포스트