최소 비용으로 유량을 보내는 경우를 찾는 문제
이 글에서 최단 경로는 항상 '최소 비용인 경로'를 뜻한다.
이 글을 읽기 위해 유량 그래프, Dinic, Bellman-ford, Dijkstra 알고리즘에 대한 이해가 있어야 한다.
이 글은 (링크)를 읽고 이해한 것을 바탕으로 작성하였다.
알고리즘
입력 : 구하는 유량의 상한 , 음수 사이클이 없는 유량 네트워크 : 각각 (그래프, 용량, 비용, 소스, 싱크)
출력 : 이하의 최대 유량, 최소 비용
- 모든 간선 의 유량을 0으로 한다 :
- 이고, 에서, 에서 로 가는 경로가 있다면 아래를 반복한다.
- a. 에서 로 가는 최단 경로 를 구한다.
- b. 에 0보다 크고 이하인 유량을 흘려보낸다. 이를 라고 하자.
- c.
- return
정리 1.
상의 가능한 두 flow 와 의 덧셈, 뺄셈은 다음과 같이 정의된다.
의 모든 간선 에 대해
: 소스에서 싱크로 흐르는 유량.
: 에 대한 비용.
이들은 음수가 될 수도 있다.
이때, 다음을 만족한다.
자세한 증명은 (여기)에
정리 2.
는 음수 사이클이 없는 네트워크이다. 이때, 가 인 flow 중 최소 비용이라면, 에는 음수 사이클이 없다. 이는 필요 충분 조건으로, 에 음수 사이클이 없다면 는 최소 비용이다.
증명 : 가 최소 비용이면 에 음수 사이클이 없다.
간단한 증명은 아래와 같다.
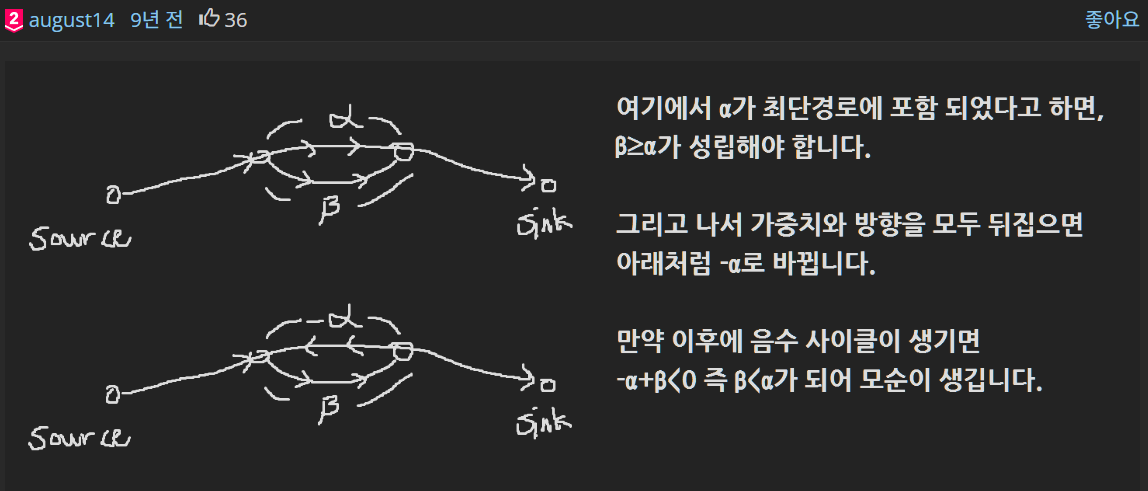
다른 방법으로도 증명할 수 있다.
가 중 최소 비용이고 에 음수 사이클이 존재한다고 가정해보자. 에 있는 음수 사이클에만 유량을 흘려 보내는 flow 를 얻을 수 있다. 이때, 다음을 만족한다.
따라서,
이는 가 중 최소 비용이라는 것과 모순되므로 에 음수 사이클이 존재할 수 없다.
증명 : 에 음수 사이클이 없으면 는 최소 비용이다.
최소 비용이 아닌 flow 을 가정해보자. 따라서 다음을 만족하는 가 존재한다.
에 value가 이고 비용이 음수인 경로, 즉 음수 사이클이 존재해야만 가 존재할 수 있다. 에 음수 사이클이 없다면 가 존재할 수 없고, 이 최소 비용이 아니라는 것과 모순이다.
정리 3.
알고리즘 진행 중 구하는 의 최단 경로의 길이는 줄어들지 않는다.
증명
알고리즘 진행 중 얻어진 flow 가 있다. 또한,
에서 최단 경로인 를 구하고 만큼 유량을 더해 flow 를 얻었다. 이후,
에서 최단 경로인 를 구하고 만큼 유량을 더해 flow 를 얻었다.
flow 가 아래와 같을 때 를 에 더할 수 있다.
의 비용이 보다 작다면 (이)가 성립한다. 이는 가 에서 최단 경로라는 것과 모순된다. 따라서 의 비용이 의 비용보다 작아질 수 없다. 즉, 를 항상 만족한다.
따라서 알고리즘 수행 도중 얻어진 의 최소 비용은 다음과 같다. 은 최대 유량
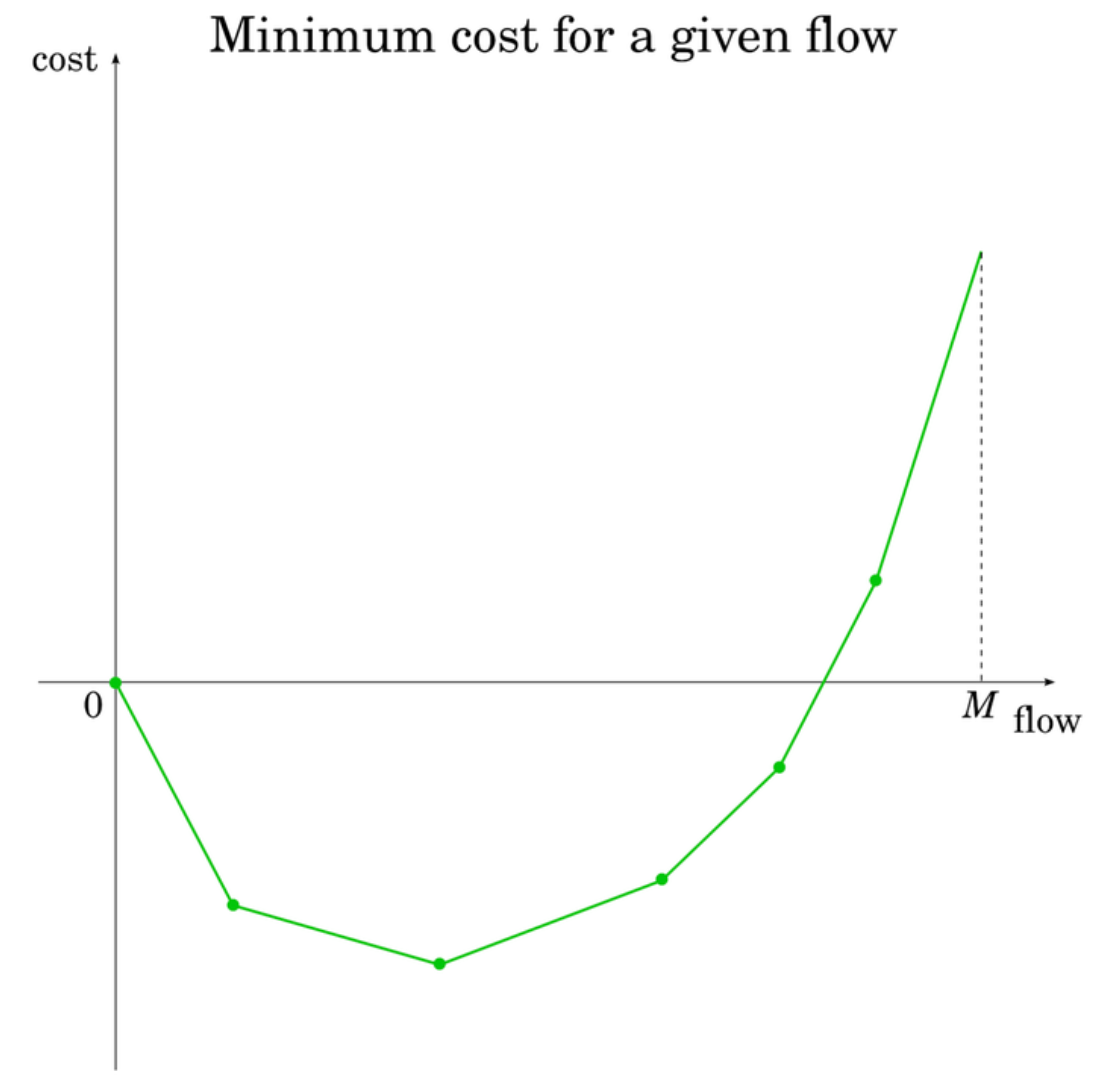
물론 cost가 음수로 내려가지 않을 수도 있다.
Dinic, Dijkstra, Potential을 사용한 MCF
알고리즘
입력 : 음수 사이클이 없는 유량 네트워크
출력 : 이하의 최대 유량, 최소 비용
- 모든 간선 의 유량을 0으로 한다 :
- Bellman-Ford로 potential 계산
- 이고, 에서, 에서 로 가는 경로가 있다면 아래를 반복한다.
- a. Dijkstra와 potential을 이용하여 shortest-path subgraph인 를 구한다. 동시에 다음 potential을 계산한다.
- b. 에서 Dinic 알고리즘을 수행한다.
- return
Potential
potential은 그래프에서 음수 간선을 없애고 다익스트라 알고리즘을 사용할 수 있게 해준다. 이를 위해 함수를 다음과 같이 mapping하자.
에서 로 향하는 간선 의 비용 이 있을 때, 를 다음과 같이 정의할 수 있다.
새로 정의한 비용인 을 적용하여 경로 의 비용을 다음과 같이 구할 수 있다.
이는 곧, 기존 비용 + (출발점과 도착점의 값 차이)와 같다.
이제 함수를 다음과 같이 정의하자.
: 에서, 에서 정점 까지의 최단 경로의 길이
이러면 모든 에 대해 를 만족한다. 이러한 를 potential이라고 부른다.
증명
정점 에서 로 향하는 간선을 라고 하자. 와 가 각각 to 의 최단 거리, to 의 최단 거리이므로, (이)가 성립한다. 즉, 이다.
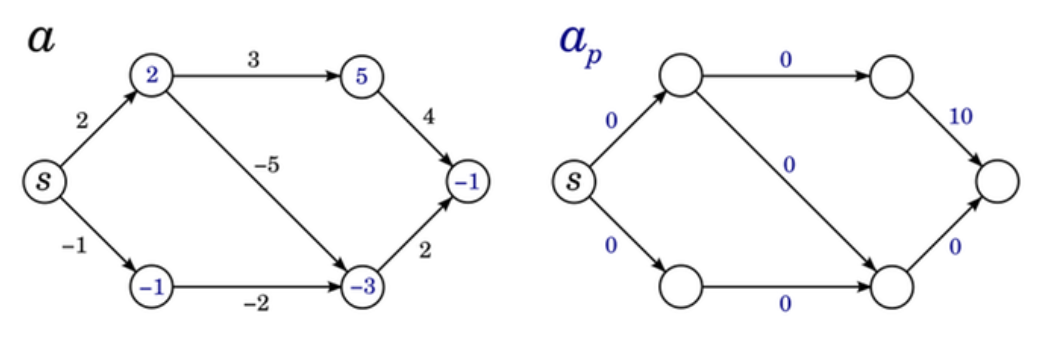
최단 경로 상의 값은 항상 0이다.
값의 갱신
알고리즘을 수행하면서 값은 계속 바뀐다. 이 또한 다익스트라로 계산할 수 있다.
새 flow 를 적용한 그래프 에서 , 에서 다익스트라로 찾은 to 최단 경로를 라고 하자.
다익스트라로 간선 를 따라 에 도착한 순간 이전 flow 의 potential을 이용한 가 얻어진다. 이므로, 이미 알고 있는 를 더해 를 구할 수 있다.
의 최댓값은 간선의 비용의 최댓값 에 정점의 개수 을 곱한 이다.
시간 복잡도
(3번 과정의) 한 반복에서 유량은 최소 1 증가한다. 유량이 1 증가할 때, Dinic알고리즘이 수행되는 데 걸리는 시간은 이고, 다익스트라는 시간이 걸린다. 매 반복마다 유량이 1씩만 증가한다면, 최대 유량인 ()만큼 반복할 것이다. 이때 시간 복잡도는 이다.
한 반복에서 유량이 2 이상 증가하는 경우가 있을 땐 계산이 매우 복잡해진다. 이때, 증가하는 유량을 라고 할 때, Dinic 알고리즘의 수행 시간은 이다. 간단히 라고 하자. 또한, 반복 횟수의 상한은 최단 경로의 길이의 최댓값 , 혹은 중 작은 것이다. 따라서 전체 시간 복잡도는 이다.
는 로 간단하게 계산할 수 있다. 은 정점의 개수이고, 는 한 간선이 가질 수 있는 비용의 최댓값이다.
간단히 라고 생각하면 될 것 같다.
체감상은 만큼 빨랐다.
구현
#include <vector>
#include <queue>
using namespace std;
const int MAXV = 802, INF=987654321;
int capacity[MAXV][MAXV], flow[MAXV][MAXV], cost[MAXV][MAXV];
vector<int> edge[MAXV], work, level, p;
// 음수 사이클이 있을 경우 텅 빈 배열을 반환
vector<int> CalcDist_BellmanFord(int n_vertex, int source, int sink) {
vector<int> upper{n_vertex, INF};
upper[source] = 0;
bool updated;
for (int iter = 0; iter < n_vertex; iter++) {
updated = false;
for (int u = 0; u < n_vertex; u++) {
for (int v : edge[u]) {
// (u, v) 간선을 따라 완화를 시도한다.
if (upper[v] > upper[u] + cost[u][v]) {
upper[v] = upper[u] + cost[u][v];
updated = true;
}
}
}
if (!updated) break;
}
if (updated) upper.clear();
return upper;
}
bool CalcDist_Dijkstra(int n_vertex, int source, int sink) {
vector<int> next_p = p;
vector<int> shortest{n_vertex, INF};
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
shortest[source] = 0;
pq.push({ shortest[source],source });
while (!pq.empty()) {
int dist_u = pq.top().first;
int u = pq.top().second;
pq.pop();
if (shortest[u] < dist_u) continue;
for (int v : edge[u]) {
if (capacity[u][v] - flow[u][v] <= 0) continue;
int dist_v = dist_u + p[u] + cost[u][v] - p[v];
if (dist_v < shortest[v]) {
shortest[v] = dist_v;
pq.push({ dist_v,v });
}
}
next_p[u] = shortest[u] + p[u];
}
p = next_p;
return shortest[sink] < INF;
}
bool BFS(int n_vertex, int source, int sink) {
level = vector<int>(n_vertex, -1);
queue<int> q;
level[source] = 0;
q.push(source);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : edge[u])
if (level[v] == -1 && capacity[u][v] - flow[u][v] > 0 && p[u] + cost[u][v] - p[v] == 0) {
level[v] = level[u] + 1;
q.push(v);
}
}
return level[sink] != -1;
}
int DFS(int u, int get, int sink, int& this_cost) {
if (u == sink)
return get;
for (int& i = work[u]; i < edge[u].size(); i++) {
int v = edge[u][i];
int residue = capacity[u][v] - flow[u][v];
if (level[v] == level[u] + 1 && residue > 0 && p[u] + cost[u][v] - p[v] == 0) {
int put = DFS(v, min(get, residue), sink, this_cost);
if (put > 0) {
this_cost += cost[u][v];
flow[u][v] += put;
flow[v][u] -= put;
return put;
}
}
}
return 0;
}
pair<int,int> MCF_Dinic(int n_vertex, int max_flow, int source, int sink) {
p = CalcDist_BellmanFord(n_vertex,source,sink);
if(p.empty()) return {-1,0}; // 음수 사이클이 존재함
int total_flow = 0, total_cost=0;
while (max_flow > 0 && CalcDist_Dijkstra(n_vertex, source, sink)) {
while (max_flow > 0 && BFS(n_vertex, source, sink)) {
work = vector<int>(n_vertex, 0);
while (max_flow > 0) {
int this_cost = 0;
int put = DFS(source, max_flow, sink, this_cost);
if (put == 0)break;
max_flow-=put;
total_flow += put;
total_cost += this_cost * put;
}
}
}
return { total_flow,total_cost };
}
void Connect(const int u, const int v, const int _capacity, const int _cost) {
edge[u].push_back(v);
edge[v].push_back(u);
capacity[u][v] = _capacity;
cost[u][v] = _cost;
cost[v][u] = -_cost;
}