실수 표현 방식

• 컴퓨터는 모든 수를 0과 1로 이루어진 2진수로 표현한다.

• 정수의 경우 이러한 표현이 간단하지만

• 실수를 2진수로 표현하는것은 복잡하며 고정 소수점과 부동 소수점 방식 총 2가지 방식이 있다.

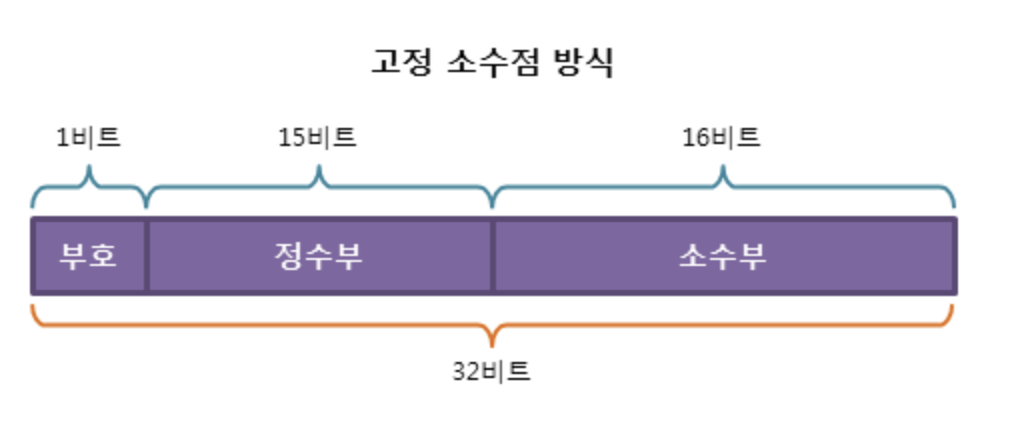
고정 소수점(fixed point) 방식

• 첫 번째 칸 = 부호비트

  음수 = 1, 양수 = 0

• 그 다음 15칸 = 정수부

  실제 정수 부분을 넣는다.

• 그 다음 16칸 = 소수부

  실제 소수 부분을 넣는다.

• 나머지칸은 0으로 채운다.

EX) 21.25 표현

• 21.25를 2진수로 변환 -> 10101.01

  소수점을 2진수 변환하는 법
  0.25 X 2 = 0.5 # 0
  0.5 X 2 = 1.0 # 1

• 부호비트 = 0

• 정수부 = 10101

• 소수부 = 01
  

• 나머지는 0으로 채우기
  

부동 소수점(floating point) 방식

IEEE 부동 소수점 방식

• 현재 사용되고 있는 부동 소수점 방식은 대부분 IEEE 754 표준을 따르고 있다.
  
  

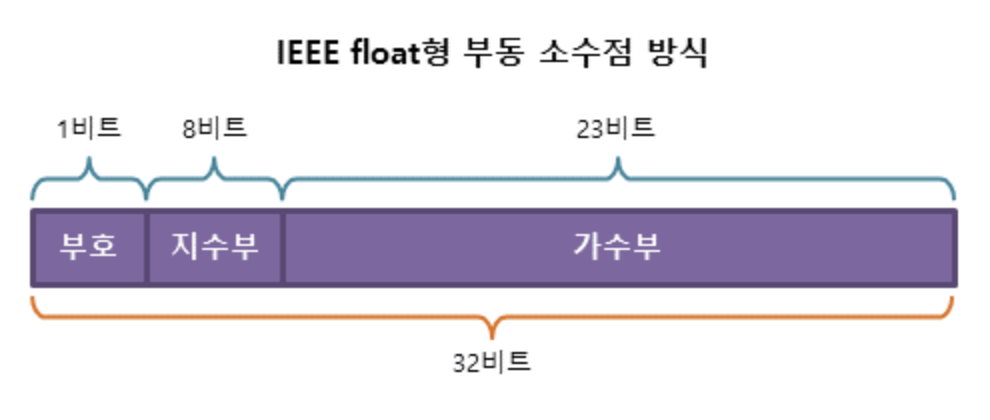
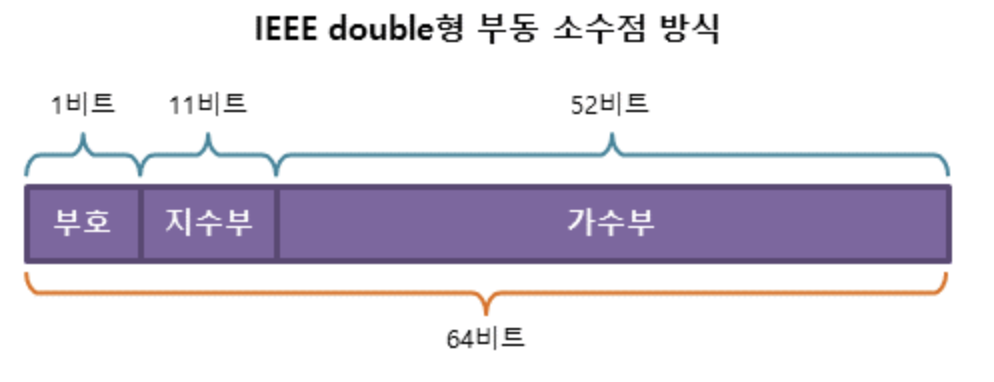
(32비트일경우 / 64비트일경우)

• 첫 번째 칸 = 부호비트

  음수 = 1, 양수 = 0

• 그 다음 (8비트 / 11비트) = 지수부

  n 에 bias를 더한 값을 2진수로 변환한 수
  bias는 32비트 = 127 / 64비트 = 1023

• 그 다음 (23비트 / 52비트) = 가수부

  m의 소수점 아래 부분

• 나머지칸은 0으로 채운다.

EX) 21.25 (32비트가정)

10진수로 먼저 알아보자
고정소수점: 123.456
부동소수점: 1.23456×10^2

R=±m×10^n

• n은 R을 m으로 만들 때 소수점을 이동한 칸 수
• IEEE 754 표현에 따라 m은 1.XXXX의 형태로 만들기로 정해짐

21.25라는 10진수를 2진수 부동 소수점으로 표현해보자

• 10진수 21.25를 2진수로 바꾼다.

  21.25→10101.01

• R,m,n 값 정리하기

  R=10101.01이다. IEEE 754에 따라 m을 구하면
  m=1.010101
  n=4

• 부호비트 = 0

• 지수부분 = 10000011(n+bias = 4+127 = 131를 2진수로 변환)

• 가수부분 = 010101

• 결과: 1.010101×2^4

  이렇게 표현하는 것을 정규화한다고 말한다.

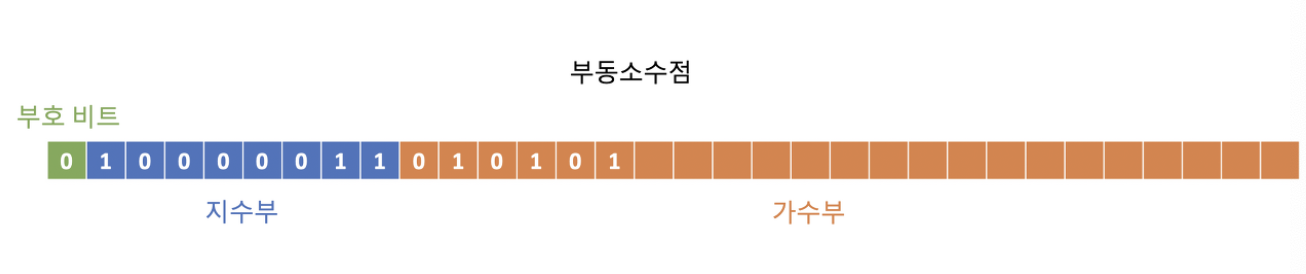
• 나머지 부분 0으로 채워주기

부동소수점의 의의

• 고정소수점

  • 정수부분과 소수부분으로 나눈다
  • 정수부분이 일정 자릿수보다 큰 수는 다룰 수 없게 된다.
  • 32비트의 경우 정수 부분이 15비트가 넘어가는 수는 다룰 수 없게 되는 것이다.

• 부동소수점

  • 정수, 소수 대신 가수, 지수로 다루기 때문에 정규화를 통해 더 큰 수를 표현할 수 있게 된다.

결론적으로 부동소수점은 고정소수점보다 큰 수를 다룰 수 있다는 데 의의가 있다.

부동 소수점 방식의 오차

• 고정 소수점 방식보다 표현 범위가 더 넓지만,
• 부동 소수점으로 표현하는 실수는 항상 오차가 존재하는 단점을 가진다.

즉, 컴퓨터에서 실수를 표현할 때는 정확한 표현이 아닌 근사치를 표현하는 것이다.

// 0.1를 1000번 더하기
double var = 0.0;
for(int i = 0; i < 1000; i++) {
	var += 0.1;
}

System.out.println(0.1 * 1000); // 100.0 출력
System.out.println(var);   // 99.9999999999986 출력

참고

https://velog.io/@jeb1225/%EC%8B%A4%EC%88%98%ED%91%9C%ED%98%84-%EB%B0%A9%EC%8B%9D-%EA%B3%A0%EC%A0%95%EC%86%8C%EC%88%98%EC%A0%90%EA%B3%BC-%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90
https://jiminish.tistory.com/81
http://www.tcpschool.com/cpp/cpp_datatype_floatingPointNumber