MST(최소 신장 트리) - Kruscal 알고리즘

MST 관련 설명은 이전 페이지인 Prim 알고리즘 페이지에 있습니다.

Kruscal 알고리즘

해당 알고리즘을 코드로 구현하려면 Union-Find 알고리즘을 알아야합니다.

전체 간선을 탐색하면서 MST를 찾는 알고리즘

과정

1. 모든 간선들을 가중치를 기준으로 오름차순 정렬
2. 간선을 하나씩 체크하는데, 만약 해당 간선때문에 사이클이 발생한다면 해당 간선은 추가하지 않는다.

   사이클을 확인할때 union-find 알고리즘을 사용합니다.

3. 사이클이 발생하지않는다면 해당 간선을 추가한다.
4. 간선을 추가하는 과정을 n-1번(전체 노드의 개수-1)만큼 반복한다.

Kruscal 알고리즘 예시

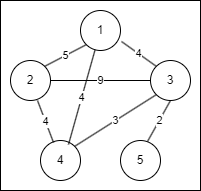
1. 가중치가 가장 낮은 3-5 간선을 추가한다. 가중치 +2 (현재 노드: 3,5 , 가중치: 2)
2. 그 다음으로 가중치가 가장 낮은 3-4 간선을 추가한다. 가중치 +3 (현재 노드: 3,4,5 , 가중치:5)
3. 그 다음으로 가중치가 가장 낮은 1-3 간선을 추가한다. 가중치 +4 (현재 노드: 1,3,4,5 , 가중치:9)
4. 그 다음으로 가중치가 가장 낮은 간선은 1-4 간선인데, 1-4 간선을 추가하면 사이클이 발생하므로, 추가하지 않는다.
5. 그 다음으로 가중치가 가장 낮은 2-4 간선을 추가한다. 가중치 +4 (현재 노드: 1,2,3,4,5 , 가중치:13)

실제 코드와 시간복잡도

class Infor {
public:
	int w;
	int s;
	int f;

	Infor() { w = 0; s = 0; f = 0; }
	Infor(int w, int s, int f) {
		this->w = w;
		this->s = s;
		this->f = f;
	}
};

bool compare(Infor a, Infor b) { return a.w < b.w; }

int Find(int x) {
	if (x == parent[x]) return x;
	else return parent[x] = Find(parent[x]);
}

int kruscal(){
    vector<int> parent; 
    // union-find 를 위한 배열
    // 부모노드의 번호를 가리킴
    
    vector<Infor> kruscal;
    // 가중치, 시작지점, 도착지점이 저장되어 있다
    
    parent.resize(v + 1);
    for (int i = 1; i <= v; i++) {
        parent[i] = i;
    }
    // 자기자신을 가리킴 -> 자기자신이 루트노드

    int s, f, w;
    for (int i = 0; i < e; i++) {
        cin >> s >> f >> w;
        kruscal.push_back({ w,s,f });
    }

    sort(kruscal.begin(), kruscal.end(), compare);
    // 모든 간선을 가중치 기준 오름차순으로 정렬

    int result = 0;
    int cnt = 0;
    int rs, rf;
    for (auto& cur : kruscal) {
        rs = Find(cur.s);
        rf = Find(cur.f);
        if (rs == rf) continue; 
        // 루트노드가 같다 -> 해당 간선을 추가하면 사이클 생성됨

        result += cur.w; 
        // MST를 구하는데 필요한 가중치를 모두 더한다
        // 다른 로직으로 변경가능

        if (rs > rf) parent[rs] = rf;
        else parent[rf] = rs;
        // 두 노드가 속한 트리를 합치는 과정 
        
        cnt++;
        if (cnt == v - 1) break;
        // 모든 정점의 개수 - 1 번 반복했다면 최적화를 위해 종료한다.
    }

    return result;
}

시간복잡도: $O(ElgE)$

모든 간선을 정렬하는데 걸리는 시간: $ElgE$

간선하나씩 탐색하면서 MST만드는 시간: $ElgE$