프로그래머스 level2 - (8)

기능개발

기능개발 문제는 스택/큐 문제이다. 이 문제를 푸는데 많은 시간을 투자했지만 결국 풀지 못했다..
자료구조에 대한 이해가 부족하다는 걸 알게되었다.

자료구조: 데이터를 효율적으로 다를 수 있는 방법의 모음!!
대표적으로 : 배열 스택 큐 연결리스트 해시테이블 그래프 트리

그렇다면 스택/큐는 어떤것일까??

스택(Stack)

먼저 스택은 쌓다라는 의미로 데이터를 차곡차곡 쌓아올린 자료구조를 말한다.

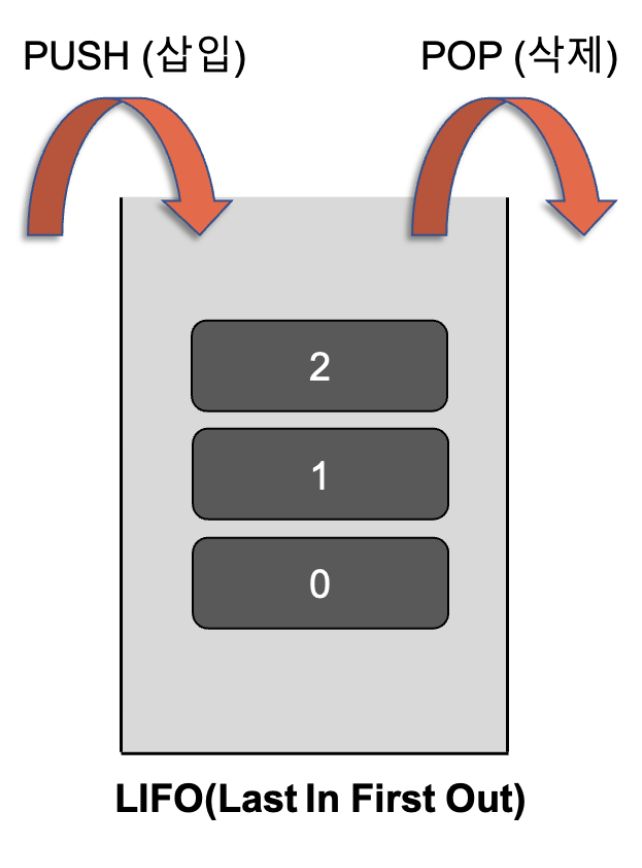
가장 마지막에 삽입된 자료가 가장 먼저 삭제되는 구조를 가지고 있다.

Last In First Out이라고도 부르며 주로 Push 메서드와 pop 메서드를 사용한 문제에 사용이된다.

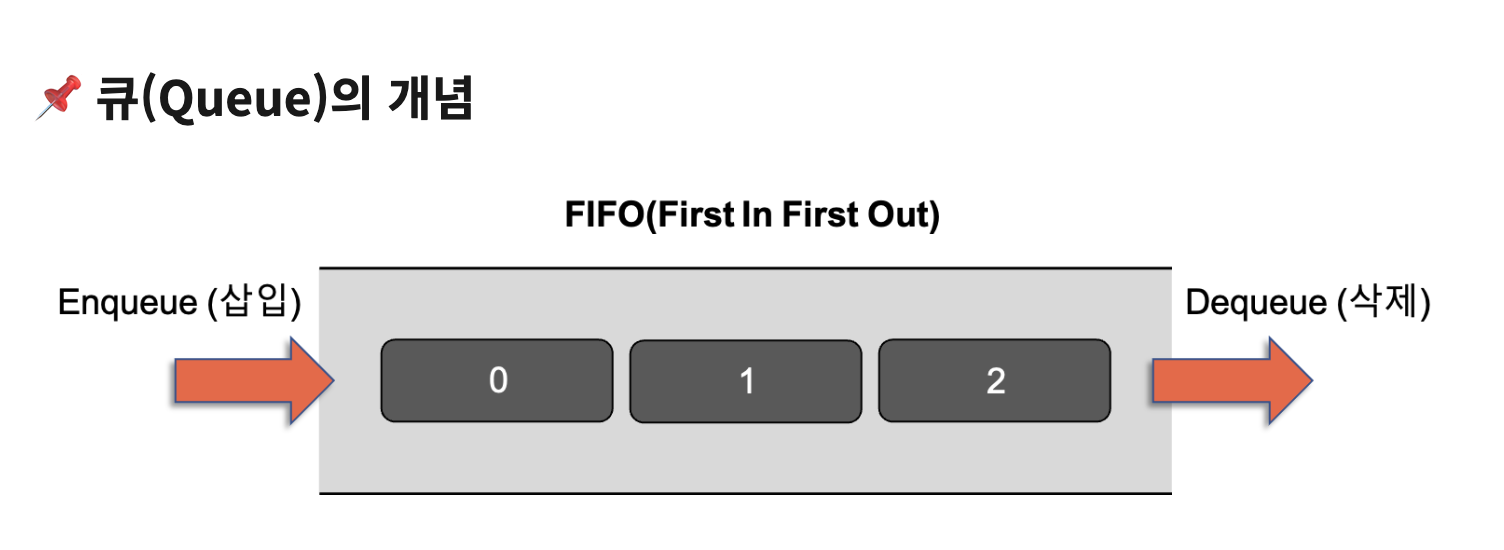
큐(Queue)

큐는 스택과 다르게 먼저들어온것이 먼저 나가는 "선입선출"로 Fitst In First Out의 구조이다.

그렇다면 이 문제에서 어떻게 스택/큐를 적용할 수 있을까

먼저 필자가 생각한 코드의 로직은 다음과 같다.

1. 개발은 앞의 기능이 완료되어야 뒤의 개발도 진행되기 때문에 맨 앞의 개발완료 유무가 중요하다.
2. 그렇기 때문에 이 점을 이용하여 progresses에 speeds를 더해가며 index 0의 원소가 100이 넘거나 같으면 progresses에서 제거(완료) 후 count 를 하나 높이자
3. 그 후 0의 index가 100보다 크다면 또 다시 count를 높이고
4. 0 index에서 100보다 작을 때 count를 push 하자

필자가 잘못 작성한 코드는 다음과 같다.

let progresses = [93, 30, 55];
let speeds = [1, 30, 5];
function solution(progresses, speeds) {
  let check = [];
  let count = 0;
  while (progresses.length > 0) {
    count = count + 1;
    progresses[0] = progresses[0] + speeds[0];
    if (progresses[0] >= 100) {
      progresses.shift();
      speeds.shift();
      check.push(count);
      count = 0;
    }
    // 하지만 이렇게 했을 때 0 인덱스 뒤 1의 인덱스가 100이 넘었더라도 카운트가 되지않는 오류가발생한다.
  }

  return answer;
}
solution(progresses, speeds);

위 로직에서 실패 한 후 는 다른 로직을 세워 보았다.

1. 차라리 개발을 완료하기 까지 남은 day를 배열로 만들어서
2. 그 배열을 순회해 크기를 비교하며 문제를 해결할 수 있지 않을까?

그렇게 짜본 코드는 실수로 지워버렸다........ 하지만 다음과 같은로직을 세웠었 던 기억은 난다

다른 사람들의 코드를 보니 위와같은 로직으로 세운 코드가 가장 많은 좋아요 수를 받았다.

나의 코드와 차이는 조금 있었지만 그래도 그냥 그렇게 계속 생각해볼 걸 이라는 아쉬움이 남았다.

다른 분의 코드는 다음과 같다.

function solution(progresses, speeds) {
    let answer = [0];
    let days = progresses.map((progress, index) => Math.ceil((100 - progress) / speeds[index]));
  // 필자는 이 부분을 while문으로 복잡하게 풀었었는데 map으로 더 단순하게 풀 수 있다는 점이 놀랐다.
    let maxDay = days[0];
// 이 부분은 같았다. 필자는 target을 변수명으로 설정하였다.
    for(let i = 0, j = 0; i< days.length; i++){
        if(days[i] <= maxDay) {
            answer[j] += 1;
        } else {
            maxDay = days[i];
            answer[++j] = 1;
        }
      // j까지 사용하여 answer[j]에 바로 넣어주는 모습이 인상깊었다. 
    }

    return answer;
}

연수부분수열합의개수

철호는 수열을 가지고 놀기 좋아합니다. 어느 날 철호는 어떤 자연수로 이루어진 원형 수열의 연속하는 부분 수열의 합으로 만들 수 있는 수가 모두 몇 가지인지 알아보고 싶어졌습니다. 원형 수열이란 일반적인 수열에서 처음과 끝이 연결된 형태의 수열을 말합니다.
예를 들어 수열 [7, 9, 1, 1, 4] 로 원형 수열을 만들면 다음과 같습니다.

입출력 예 #1
길이가 1인 연속 부분 수열로부터 [1, 4, 7, 9] 네 가지의 합이 나올 수 있습니다.
길이가 2인 연속 부분 수열로부터 [2, 5, 10, 11, 16] 다섯 가지의 합이 나올 수 있습니다.
길이가 3인 연속 부분 수열로부터 [6, 11, 12, 17, 20] 다섯 가지의 합이 나올 수 있습니다.
길이가 4인 연속 부분 수열로부터 [13, 15, 18, 21] 네 가지의 합이 나올 수 있습니다.
길이가 5인 연속 부분 수열로부터 [22] 한 가지의 합이 나올 수 있습니다.
이들 중 중복되는 값을 제외하면 다음과 같은 18가지의 수들을 얻습니다.
[1, 2, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 20, 21, 22]

즉, 수열에서 더하는 경우의 수 문제였다.

필자가 세운 로직은 다음과 같다.

1. 중복은 마지막에 제거하면 된다.
2. 반복문은 이중반복문을 활용하여 각 반복문에 따라 더하는 조건을 다르게하여 합을 배열에 push
3. 마지막으로 배열에서 중복을 제거한 후 return 하자

필자가 작성한 코드는 다음과 같다.

function solution(elements) {
  const elementsLength = elements.length;
  const answer = [];

  for (let i = 0; i < elements.length; i++) {
    //i는 1~5까지의 길이를 더해야함으로
    let sum = 0;
    let count = 0;
    for (let j = 0; j < elements.length + i; j++) {
      
      //j는 세부 길이를 조절하는 역할
      count = count + 1;
      sum = sum + elements[j % elementsLength];
      if (count > i) {
        answer.push(sum);
        count = 0;
        sum = 0;
        j = j - i;
        // j에서 i만큼을 감소시켜 반복문의 폭을 넓혔다.
      }
    }
  }
  return [...new Set(answer)].length;
  // 중복원소제거
}

K진수소수개수구하기

다음 문제는 그냥 알고리즘 문제로 다음과 같은 로직을 세웠다.

1. N 을 K 진수로 변환하자
2. 그 후 0을 먼저 찾자
3. 변환 된 N을 순회하며 0을 만나기 전엔 해당 인덱스 까지의 string을 target으로 설정하자
4. 해당 target의 소수 검열을 한 후 소수면 answer Arr 에 push하자

위 로직으로 문제를 해결하려 했는데 0을 찾아야되는 번거로움과 소수판별을 하는데 분제점을 발견하였다.

먼저 0을 찾지 않아도 되는 방법이 있다.

바로 split("0") 을 적용 시켜 0을 기점으로 숫자를 나누어 배열의 형태로 반환하면 된다.
그 후 그 배열을 순회하며 소수검열을 시작하면 더 간단하게 문제를 해결 할 수 있다!

또, 기존에 필자가 사용했 던 소수 판별 함수는 다음과 같다.

function checkPrime(numbers) {
  if (numbers < 2) {
    return false;
  }
  for (let i = 2; i <numbers; i++) {
    if (numbers % i === 0) {
      return false;
    }
  }
  return true;
}

다음과 같이 테스트를 돌렸을 땐 실패로 결과가 도출되었지만

function checkPrime(numbers) {
  if (numbers < 2) {
    return false;
  }
  for (let i = 2; i <= Math.sqrt(numbers); i++) {
    if (numbers % i === 0) {
      return false;
    }
  }
  return true;
}

Math.sqrt메서드를 활용하여 루트를 씌운 결과 값에 적용을 시키니 통과되었다.

위 Math.sqrt메서드를 사용하면 for문의 순회도 줄어들고 정확성도 올라간다

최종 코드는 다음과 같다.

let n = 437674;
let k = 3;

function checkPrime(numbers) {
  if (numbers < 2) {
    return false;
  }
  for (let i = 2; i <= Math.sqrt(numbers); i++) {
    if (numbers % i === 0) {
      return false;
    }
  }
  return true;
}

function solution(n, k) {
  let answer = [];
  n = n.toString(k).split("0");

  n = n.filter((num) => checkPrime(num*1));
  //num에 1을 곱해준 이유는 만약 변환된 n이 100일 경우 [1,"",""] 이렇게 나오기 때문에
  // 숫자 1을 곱해 소수판별을 시행한다

  return n.length;
}

solution(n, k);