땅따먹기
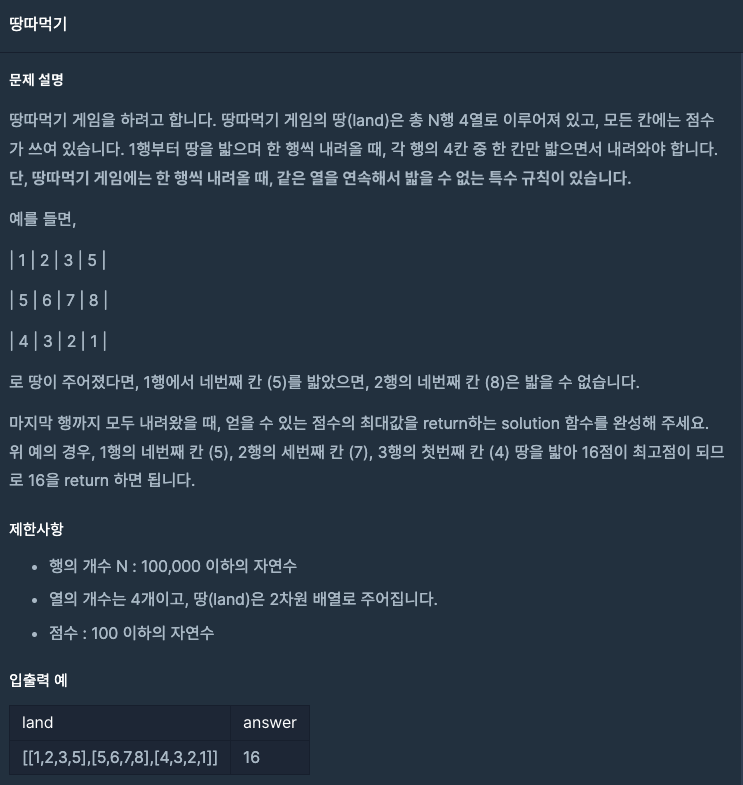
해당 문제는 처음에 봤을 때 "어? 꽤 쉬운데 왜 정답률이 높지않지?" 라는 생각을 했었다.🥲
코드를 완성하고 제출을 해보니 결과는!! 💯? 0점!!!
ㅋㅋ
왜 그랬나 봤더니 필자의 처음 로직이 완전히 잘못 됐음을 알게되었고 이 문제는 DP(동적다이나믹계획법)
으로 해결해야 한다는 걸 알게되었다.
필자가 처음 잘못 생각했던 로직은 다음과 같다.
- land 배열을 순회하며 각 행의 최댓값을 구한다.
- 최대값의 index를 기억하고 다음 배열을 순회할 때는 해당 행의 최대값이 저장한 index가 아니면 그대로 누적한다.
- 행의 최대값이 저장한 index라면 해당 index요소를 -1 로 변경 시킨 뒤 다시 최대값을 구한 뒤 누적한다.
- 이를 반복문을 통해 반복한다.
이는 잘못된 로직이다. 왜냐하면 결국 이는 경우의 수 문제이기 때문이다
2행에서 최대값과 3행에서 최대값을 더하는 경우가 전체적으로 봤을 때 최대값이 아닐 수 있다는 말이다.
왜냐하면 [[1,2,3,4,5], [2,2,3,1,10]] 의 배열이있을 때 1행의 최대값은 5 해당 index가 아닌 2행의 최대값은 3 이다 . 그러나 1행을 4로 설정하면 2행에서 10을 선택할 수 있다.
그렇기 때문에 이 문제는 앞뒤의 행이 서로 연관관계에있다.
잘못 풀었던 코드는 다음과 같다.
function solution(land) {
let answer = 0;
let target;
for (let i = 0; i < land.length; i++) {
let Max = Math.max(...land[i]);
let MaxIndex = land[i].indexOf(Max);
let MaxLastIndex = land[i].lastIndexOf(Max);
if (MaxIndex !== MaxLastIndex) {
target = -1;
answer = answer + Max;
continue;
}
if (MaxIndex === target) {
land[i].splice(MaxIndex, 1, 0);
Max = Math.max(...land[i]);
MaxIndex = land[i].indexOf(Max);
}
target = MaxIndex;
answer = answer + Max;
}
return answer > 100 ? 100 : answer;
}
해당 로직은 구현했지만 로직 자체가 잘못되어 실패했다,,
뭔가 이 문제는 지금 혼자 끙끙대단 너무 오래걸릴 거 같아서 정답을 미리 보았다. 처음엔 정답을 보아도 무슨말인지,, Dp가 무슨 말인지 몰라서 다양한 블로그와 유튜브 영상을 찾아봤다.
내가 먼저 이해했던 건 이 문제의 풀이법이다.
load 배열을 새로 갱신(더해가며) 풀어야하는 문제였다.
즉 , 점화식 처럼 앞 뒤의 상관관계에 있는 문제이다. 알고보니 이와 같은 알고리즘을 동적계획법(dp)라고 한다.
먼저 1행을 제외하고 2행부터는 앞의 행의 영향을 받는다. 그렇기 때문에 Index가 같지않은 다른 요소중 최대값을 해당요소에 더해가면 되는 문제이다. 말로 설명이 어려워 그림으로 그려보았다.
각 index가 같지 않은 선에서 위 행의 최대값을 해당 index에 더해주면 된다.
사실 이를 이해하는데 가장 많은 도움을 얻은 블로그가 있다.
도움받은블로그
이를 코드로 표현해보면 다음과 같다.
function solution(land) {
let answer;
for (let i = 1; i < land.length; i++) {
land[i][0] =
land[i][0] + Math.max(land[i - 1][1], land[i - 1][2], land[i - 1][3]);
land[i][1] =
land[i][1] + Math.max(land[i - 1][0], land[i - 1][2], land[i - 1][3]);
land[i][2] =
land[i][2] + Math.max(land[i - 1][0], land[i - 1][1], land[i - 1][3]);
land[i][3] =
land[i][3] + Math.max(land[i - 1][0], land[i - 1][1], land[i - 1][2]);
}
answer = land[land.length - 1];
return Math.max(...answer);
}위 코드를 보면 본인 index를 제외하고 다른 index에 있는 것들을 더해주며 각 순회가 일어날 때마다 land가 새로 업데이트 되었다.
Dp(동적계획법)이 도대체 무엇일까❓
동적 계획법은 어떤 상황에서 쓸 수 있을까?
- DFS/BFS로 풀 수 있지만?? 너무 체크해야하는 것이 많은 경우
-패턴을 찾아보면 DFS/BFS를 알아볼 수 있다. - 경우의수에 중복연산이 많은 경우
결국 경우의 수 문제인데 앞 뒤의 상관관계가 짙을 때 사용하기 좋다고 필자는 판단한다.
DP를 "기억하기" 알고리즘 이라고 생각할 수 있다고한다.
위 문제처럼 for문의 순회가 돌 때마다. 최대값과 더해진 값을 기억하고 수정한다. 또, 점화식과 같이 앞과 뒤가 어떤 수식으로 연결이 가능할 때 사용할 수 있다.
유튜버의 말로도 DP를 완벽하게 이해하기는 꽤 힘들다고한다. 필자는 이렇게 기억하려고한다.
DP는 기억하기 알고리즘! BFS/DFS에서 중복이 많을 때 사용하면 좋은 알고리즘 !
오픈채팅방
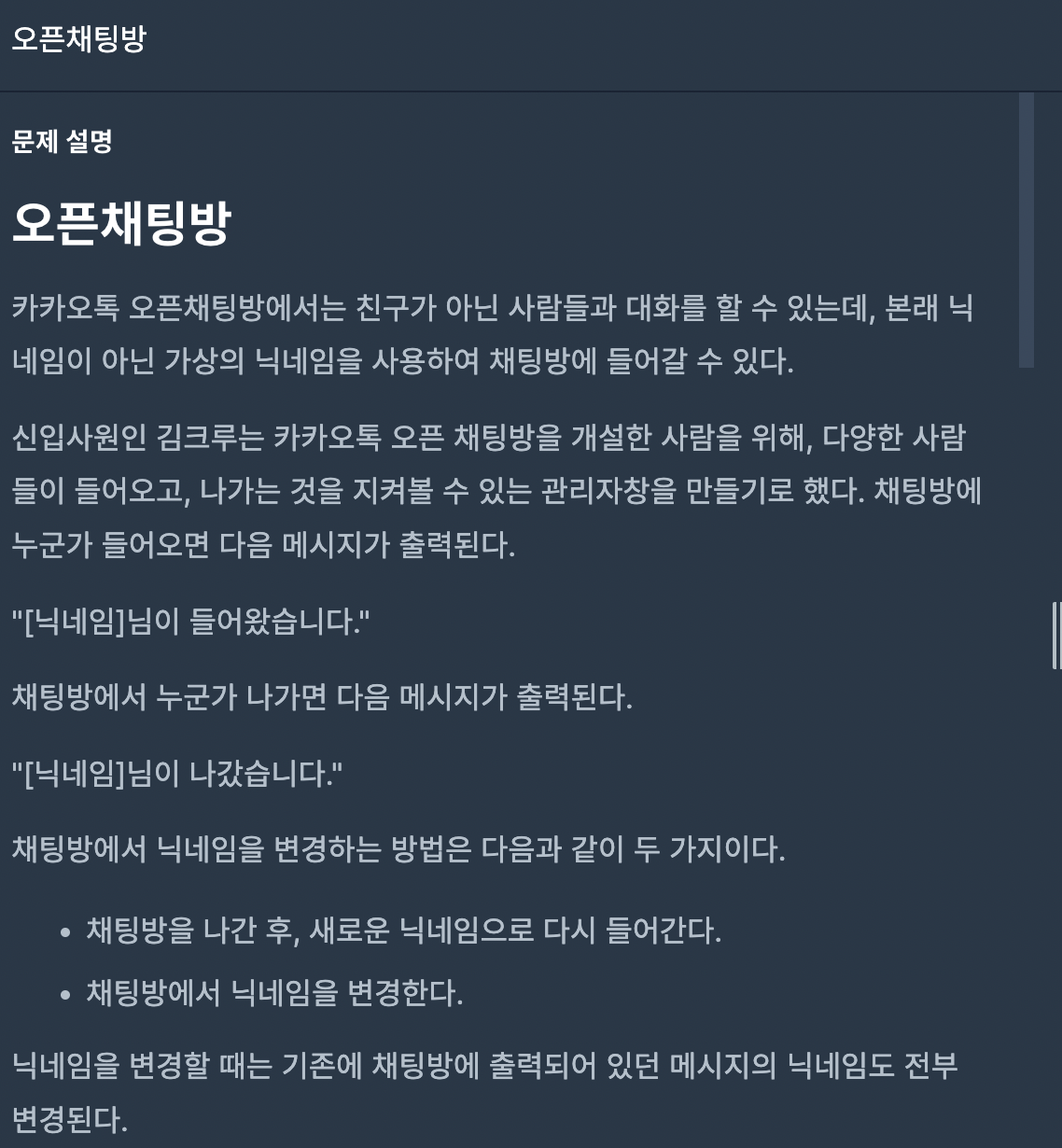
위 문제에서 닉네임을 바꿀 수 있는 경우는 2가지가 있다.
1. 채팅방을 나간 후 새로운 닉네임으로 입장(ENTER) 하는 경우
2. 채팅방에서 새로운 닉네임으로 변경(CHANGE) 하는 경우
위 두 가지 상황을 주의하며 코드를 짜보았다.
먼저 id와 nickname을 기억해야겠다는 생각으로 new Map 메서드를 사용하였다.
배열에서 불변하는 것은 id이기 때문에 이를 기억하는 게 중요했다. 특히, 들어오거나 변경할 때 id와 묶인 nickname을 바꿔주면 될 것이라는 생각이 먼저 들었다.
그렇기 때문에 record의 배열을 순회하며 기억된 id와 내가 저장한 new map의 id를 일치시켜
그 id와 저장된 nickname을 불러오면 되겠다는 생각을 했다 .
즉, record를 순회하여 각 입장 퇴장 변경에 따라 nickname을 다르게 출력하면 되겠다! 생각했다.
필자가 짠 코드는 다음과 같다.
function solution(record) {
record = record.map((item) => item.split(` `));
const answer = [];
let info = new Map();
record.forEach((item) => {
if (item[0] !== "Leave") {
info.set(item[1], item[2]);
}
});
info = [...info];
const infoId = info.map((item) => item[0]);
record.forEach((item) => {
const recordId = infoId.indexOf(item[1]);
if (item[0] === "Enter") {
answer.push(`${info[recordId][1]}님이 들어왔습니다.`);
} else if (item[0] === "Leave") {
answer.push(`${info[recordId][1]}님이 나갔습니다.`);
}
});
return answer;
}위 코드는 97점으로 완전히 통과하지 못했다.
사실 70점대에서 부터 리팩토링(이중for문 제거 , if문 최소화, for문 대신 forEach사용) 등
노력했지만 한개의 테스트 케이스에서 타임오류로 실패했다.
지금도 계속 고민하고 있지만 이 문제가 어디를 고쳐야할지 고민을 하고 있다.
리팩토링하면서도 실력을 기를 수 있어서 좋았지만 100점이 아니라..많이 아쉬운 느낌이다.. 계속 고민을 해
추후에 추가 포스팅을 해야할 거 같다!
