
알고리즘 학습 리스트 중 완전탐색이 있다. 아직 완전탐색 차례가 아니지만 완전탐색에 대한 포스팅을 먼저 올리는 이유는 ..! 전부터 DFS/BFS, 재귀함수 등에 대한 관심이 있었고 잘 하고싶었는데 이번 문제를 풀며 그래도 재귀함수에 대한 이해가 전보다 꽤 늘었구나 하고 뿌듯하기도하고 또 정리해 놓고 싶었기 때문이다. 위 문제를 기점으로 완전탐색에 대한 학습을 이어나가보겠다..!
개념은 이번주내로 포스팅 할 계획이다!
오늘 풀이한 문제는 바로!
무인도 여행 ❓
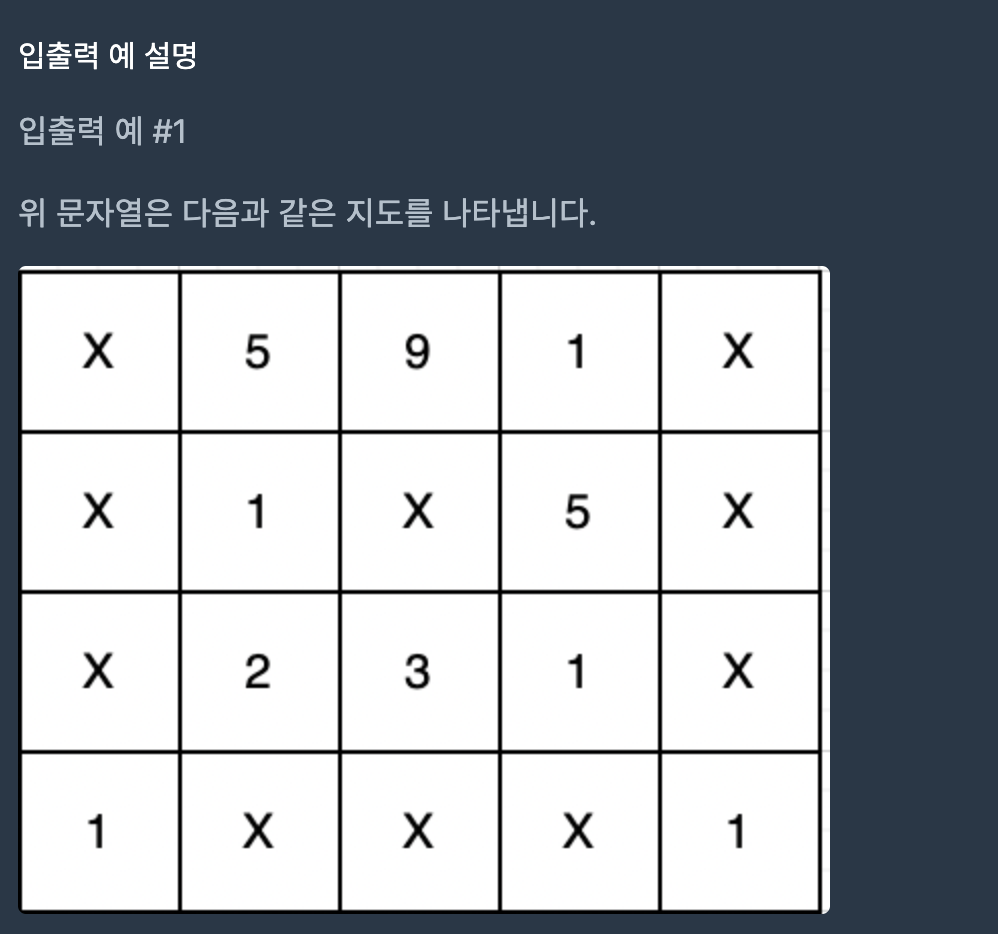
필자는 주로 이런 문제를 어려워했다. 길 찾기, 최단거리찾기, 경우의 수를 구하기. 근데 결국 이런 문제는 완전탐색문제와 가깝다..!
일단 이 문제에서 완전탐색 알고리즘을 사용할 수 있었던 이유는 Input이 매우 작았다.

10^2 의 Input이니 넉넉하게 시간복잡도를 계산해서 문제를 해결할 수 있을 것이라 생각했다.
어떻게 풀까 ❓
고민을 하다가 방문처리와 재귀함수를 사용하면 문제를 해결할 수 있을 거 같았다. 그럼 위 배열에 맞는 방문처리배열을 만들어야 한다.
maps.forEach((item) => {
const visitedArr = Array.from({ length: item.length }, () => false);
visited.push(visitedArr);
});
다음과 같이 visited를 만들어주었다.
[XXXXX,XXXXX,XXXXX,XXXXX,XXXXX,XXXXX]의 maps가 있다면
visited => [[false,false,false,false,false],[false,false,false,false,false],[false,false,false,false,false],[false,false,false,false,false],[false,false,false,false,false],[false,false,false,false,false]]
의 방문 기록을 남길 수 있는 것이다.
첫 번째 시도 ❗️
let maps = ["332XX", "1X4XX", "X16X8", "5X2XX"];
function solution(maps) {
// Index를 둘로 나눠서 UD, RL 을 control하며
// 재귀를 돌려보자
if ([...new Set(maps)].length === 1 && maps[0].includes("X")) {
return [-1];
}
let answer = [];
let visited = [];
maps.forEach((item) => {
const visitedArr = Array.from({ length: item.length }, () => false);
visited.push(visitedArr);
});
maps = maps.map((item) => item.split(``));
let sum = 0;
const dfs = (UD, RL) => {
if (
UD < 0 ||
UD >= maps.length ||
RL < 0 ||
RL >= maps[0].length ||
maps[UD][RL] === "X"
) {
return;
}
if (maps[UD][RL] !== "X" && !visited[UD][RL]) {
visited[UD][RL] = true;
dfs(UD + 1, RL,sum + maps[UD][RL] * 1;);
dfs(UD - 1, RL,sum + maps[UD][RL] * 1;);
dfs(UD, RL + 1,sum + maps[UD][RL] * 1;);
dfs(UD, RL - 1,sum + maps[UD][RL] * 1;);
}
};
for (let i = 0; i < maps.length; i++) {
for (let j = 0; j < maps[0].length; j++) {
dfs(i, j, 0);
// 움직인다는 것은 ?? 결국 끊어졌다는 거
// 이때 최대값을 ?
if (sum !== 0) {
answer.push(sum);
}
sum = 0;
}
}
answer = answer.sort((a, b) => a - b);
return answer;
}
solution(maps);
완전히 처음 시도한 코드는 아니지만( 저장하지 못했다..)
여기서 핵심은 ! dfs를 사용했고 테스트 케이스도 통과했지만 20점이 나왔다는거!
왜 그랬을까 분명 예외사항이 있으니까 그랬겠지..
이유는 다음과 같았다.
dfs(UD + 1, RL,sum + maps[UD][RL] * 1;); dfs(UD - 1, RL,sum + maps[UD][RL] * 1;); dfs(UD, RL + 1,sum + maps[UD][RL] * 1;); dfs(UD, RL - 1,sum + maps[UD][RL] * 1;);
위 부분을 보면 sum+maps[UD][RL]*1을 매개변수로 받아 dfs가 그 시점의 sum을 기억하도록 한다. 여기서 잘못 된 것이다. 문제는 모든 섬이 연결된다면 그 연결 지점은 모두 더해야하는데 막다른 길이 놓인 섬이 다시 뒤나 옆에있는 섬으로 갈때는 그 시점의 sum으로 되돌아가버려 모든 섬이 더해지지 않는 다는 점이다..!
예를들어 다음과 같은 섬이 있다고 가정해보겠다.
[X, 1, X, X, X]
[X, 1, 2, X, X]
[4, 1, X, 3, X]
[X, 1, X, 2, X]
결과가 어떻게 나올 거 같나? 먼저 왼쪽 섬이 1 + 1 + 2 + 1 + 4 + 1
이 더해져야할 거 같지만 정답은 그렇지 않다.
1 + 1 + 1 + 4 가 나온다. 왜냐하면 되돌아 가면 ?? 그 Sum은 다시 그 시점으로 돌아가니까!!
그럼 어떻게 해야겟나?? sum을 매개변수로 받는 것이 아닌 sum을 dfs외부에서 저장해주고 일정 조건이 되면 그 sum을 push해준 후 reset 해주어야한다. sum을 외부에 두어 다시 back으로 돌아가더라도 sum이 되돌아갈 여건을 마련하지 않는 것이 핵심이다.
수정한 코드는 다음과 같다.
두 번째 시도 ❗️(성공)
function solution(maps) {
// Index를 둘로 나눠서 UD, RL 을 control하며
// 재귀를 돌려보자
if ([...new Set(maps)].length === 1 && maps[0].includes("X")) {
return [-1];
}
let answer = [];
let visited = [];
maps.forEach((item) => {
const visitedArr = Array.from({ length: item.length }, () => false);
visited.push(visitedArr);
});
maps = maps.map((item) => item.split(``));
let sum = 0;
const dfs = (UD, RL) => {
if (
UD < 0 ||
UD >= maps.length ||
RL < 0 ||
RL >= maps[0].length ||
maps[UD][RL] === "X"
) {
return;
}
if (maps[UD][RL] !== "X" && !visited[UD][RL]) {
visited[UD][RL] = true;
sum = sum + maps[UD][RL] * 1;
dfs(UD + 1, RL);
dfs(UD - 1, RL);
dfs(UD, RL + 1);
dfs(UD, RL - 1);
}
};
for (let i = 0; i < maps.length; i++) {
for (let j = 0; j < maps[0].length; j++) {
dfs(i, j, 0);
// 움직인다는 것은 ?? 결국 끊어졌다는 거
// 이때 최대값을 ?
if (sum !== 0) {
answer.push(sum);
}
sum = 0;
}
}
answer = answer.sort((a, b) => a - b);
return answer;
}다음과 같이 sum을 외부에 두고 리셋을 하며 섬의 합계를 구한다.
for (let i = 0; i < maps.length; i++) {
for (let j = 0; j < maps[0].length; j++) {
dfs(i, j, 0);
// 움직인다는 것은 ?? 결국 끊어졌다는 거
if (sum !== 0) {
answer.push(sum);
}
sum = 0;
}
}위 주석을 보면 움직인다는 것은? 끊어졌다는게 무슨말이냐면
결국 위 dfs를 통해 시작점이 어디든 배열의 전체 이어진 섬을 모두 방문하게 된다. 그렇다면 시작점만 다를 뿐이지 이미 방문한 섬은 또 방문할 수 없다.
그렇기에 j가 변한다는 건 한번 j를 기점으로 쭉 돌아본 것이니 j가 변경될 때마다 sum을 더해올 것이다. 그럼 sum이 0이라는 건? 그 시점에서 무인도는 없었다는 거!
여기서 한 가지 더 알게된 사실이 있다.
배열의 Index관리는 중요해 ❗️
항상 dfs의 특히 경로 문제에서 index가 -1이 되고 length를 넘어서버리는 경우를 통제하는 방법을 잘 몰랐던 거 같다.
이 문제를 풀며 그 방법을 알게됐다.
const dfs = (UD, RL) => {
if (
UD < 0 ||
UD >= maps.length ||
RL < 0 ||
RL >= maps[0].length ||
maps[UD][RL] === "X"
) {
return;
}
if (maps[UD][RL] !== "X" && !visited[UD][RL]) {
visited[UD][RL] = true;
sum = sum + maps[UD][RL] * 1;
dfs(UD + 1, RL);
dfs(UD - 1, RL);
dfs(UD, RL + 1);
dfs(UD, RL - 1);
}
};배열에 -1이나 없는 index가 들어가면 바로 undefined어쩌고 하면서 오류가 발생한다 ㅋㅋ
그럼 index로 넣어주기 전에 return을 해버리면 ?? 문제가 없다.
처음엔 각 index에 따라 dfs를 다르게 호출하였다. 즉, if문을 사용해서 UD===0 && RL===0이면 ? dfs의 매개변수도 다르게 호출을 했었는데 생각해보니 그럴 필요가 없이
dfs 함수 맨위에서 index에 대한 통제를 해주면 된다. 위 코드는
UD<0 || UD >= <maps.length || RL<0 || RL>=maps[0].length
인 경우에 return을 해버려 따로 매겨변수를 조절하지 않아도 되게끔 했다.
코드가 훨씬 깔끔하고 경로문제에 대한 자신이 생겼다..!!!
엇 생각난김에 게임 맵 최단거리 문제를 다시 풀어봐야겠다..!

가장 최근에 풀어봤던 결과물은 다음과 같다.
게임 맵 최단거리 ❓
문제는 이전에도 풀어봤었지만 다시보니 또 새로운 느낌이었다

저 왕관 까만 로봇자식.. 알아서 찾아가줬으면 ㅋㅋ
다시 풀었는데 코드와 그 결과는 변함이 없었다 ..
function solution(maps) {
//visited를 먼저 만든다.
const visited =[]
maps.forEach((item)=>{
const visitedArr = Array.from({length: item.length},()=>false)
visited.push(visitedArr)
})
const answer = []
const dfs=(UD,RL,sum)=>{
if(UD<0 ||RL<0 || UD >=maps.length || RL>maps[0].length || maps[UD][RL]===0 ){
return;
}
if(UD===maps.length-1 && RL===maps[0].length-1){
answer.push(sum+1)
}
if(maps[UD][RL]===1 && !visited[UD][RL]){
visited[UD][RL]=true
dfs(UD+1,RL,sum+maps[UD][RL]*1)
dfs(UD,RL+1,sum+maps[UD][RL]*1)
dfs(UD-1,RL,sum+maps[UD][RL]*1)
dfs(UD,RL-1,sum+maps[UD][RL]*1)
visited[UD][RL]=false
}
}
dfs(0,0,0)
if(answer.length===0){
return -1
}
return Math.min(...answer)
}
하하하하 다른 점이 있다면 ? 이번엔 다른 분의 코드를 보지 않고 스스로 생각했다는 점
알고보니 이 문제는 DFS로는 통과가 불가능하고 BFS 알고리즘을 사용해서 해결해야한다. 위 무인도 여행 문제와 거의 비슷하고 위 문제는 sum을 그때그때 기억한다는 다른 점이 있다.
비록 문제를 통과하진 못했지만 이젠 답지없이도 저렇게 코드를 생각할 수 있음에 감사하다 ✨
완전탐색 알고리즘을 학습한 후에는 DFS/BFS에 대해 숙지할 것인데 그때 이 문제를 다시 풀어봐야겠다..!
