- 레이트레이싱
4.1. 기초 알고리즘
4.2. 원근법 (perspective)
4.3. 가시광선 연산
4.4. 광선-객체 교차점
4.5. 셰이딩
4.6. 레이트레이싱 프로그램
4.7. 그림자
4.8. 이상적인 정반사
4. 레이트레이싱
그래픽스의 기본 작업은 3차원 오브젝트 렌더링인데, 이를 통해 3차원 공간의 많은 기하학적 오브젝트로 구성된 장면 혹은 모델을 다루고, 특정 뷰포인트 (viewpoint)에서 바라본 오브젝트를 보여주는 2D 이미지를 생성함.
이 작업은 오래전부터 건축가와 엔지니어들이 설계를 다른 사람에게 전달하기 위해 그림을 그리는 것과 동일한 작업임.
기본적으로 렌더링은 입력으로 오브젝트의 집합을 받아 출력으로 픽셀 배열을 생성하는 과정임. 각 오브젝트가 픽셀에 기여하는 방식은 크게 두 가지로 나눌 수 있음.
오브젝트 순서 렌더링 (object-order rendering)에서 각 오브젝트는 순서대로 다뤄지고, 오브젝트마다 영향을 미치는 모든 픽셀을 찾고 업데이트함.
이미지 순서 렌더링 (image-order rendering)에서 각 픽셀은 순서대로 다뤄지며 픽셀마다 영향을 미치는 모든 오브젝트를 찾고 픽셀값을 계산함.
두 방식의 차이를 중첩된 루프 측면에서 생각할 수 있음. 이미지 순서 렌더링에서는 "각 픽셀"이라는 루프가 외부에 있는 반면, 오브젝트 순서 렌더링에서는 "각 오브젝트"라는 루프가 외부에 존재함.
이미지 순서/오브젝트 순서 렌더링은 같은 이미지를 연산할 수 있지만, 이들은 서로 다른 종류의 이펙트를 계산하는 데 적합하며, 전혀 다른 성능을 보여줌.
그 중 이미지 순서 렌더링은 작업이 단순하고 유연하게 이펙트를 생성할 수 있으며, 비슷한 이미지를 만드는 데 훨씬 더 많은 실행 시간이 소요된다는 특징이 있음.
레이트레이싱 (ray tracing)은 3D 장면 렌더링을 위한 이미지 순서 알고리즘임.
4.1. 기초 알고리즘
레이트레이싱은 한 번에 한 픽셀씩 연산하며, 각 픽셀에 대해 기본적인 작업은 이미지에서 해당 픽셀 위치에 표시되는 오브젝트를 찾는 것임. 각 픽셀은 다른 방향에서 보이며, 픽셀이 바라보는 모든 오브젝트는 viewing ray (뭐라고 번역해야할지 모르겠다..ㅎㅎ)를 교차해야 함. viewing ray란 픽셀이 바라보는 방향의 뷰포인트에서 나오는 직선을 말함. 특정 오브젝트가 뒤에 있는 다른 오브젝트의 시야를 차단하기 때문에, 해당 오브젝트는 카메라와 가장 가까운 viewing ray를 교차함.
오브젝트를 찾고 나면 셰이딩 (shading) 연산을 통해 교차점, 표면 법선, 혹은 다른 정보 (렌더링 타입에 따라 다름)를 사용하여 픽셀의 색상을 결정함.
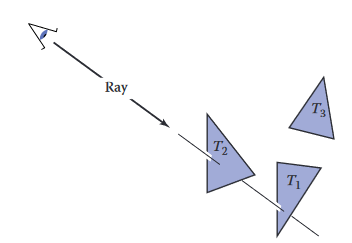
위 그림에서 광선이 두 삼각형 와 교차하지만, 가장 먼저 교차하는 삼각형 만을 셰이딩함.
기본적인 레이트레이싱은 다음 3가지 과정으로 이루어짐.
- 광선 생성 (ray generation): 카메라 기하학을 기반으로 각 픽셀이 갖는 viewing ray의 원점과 방향을 계산함.
- 광선 교차 (ray intersection): viewing ray와 교차하는 오브젝트 중에 가장 가까운 오브젝트를 찾음.
- 셰이딩 (shading): 광선 교차를 수행한 결과에 따라 픽셀의 색상을 계산함.
이를 적용한 레이트레이싱의 기본 구조는 다음과 같음.
for each pixel do
compute viewing ray
find first object hit by ray and its surface normal "n"
set pixel color to value computed from hit point, light, and "n"4.2. 원근법 (perspective)
3차원 상의 물체나 장면을 2차원 상의 그림으로 표현하는 것의 문제점은 컴퓨터가 등장하기 수백년 전부터 예술가들이 연구하던 주제였음. 사진 또한 3차원 장면을 2차원 이미지로 표현하는 것.
입체 회화 (cubist painting)부터 어안 렌즈 (fisheye lens)와 주변 카메라를 연결하는 방법까지 이미지를 만드는 파격적인 방법이 존재하지만, 예술 및 사진 분야 뿐만 아니라 그래픽스에서도 표준으로 많이 쓰는 접근법은 선 원근법 (linear perspective)임.
선 원근법은 장면 (3차원)에서의 직선이 이미지 (2차원)의 직선이 되도록 하여 3차원 상의 물체를 2차원 상의 이미지 평면 (image plane)에 투영 (project)하는 방식임.
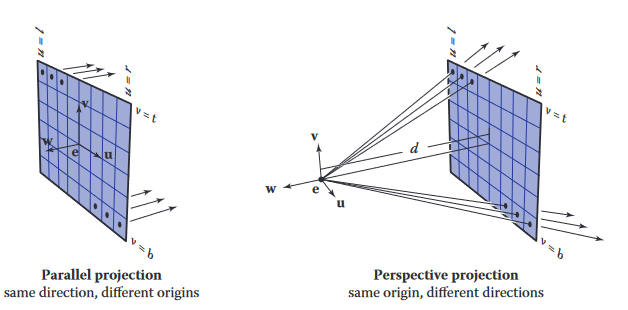
가장 간단한 투영은 평행 투영 (parallel projection)으로, 이미지 평면에 닿을 때까지 투영 방향 (projection direction)을 따라 이동하여 3차원 점을 2차원에 매핑하는 방식.
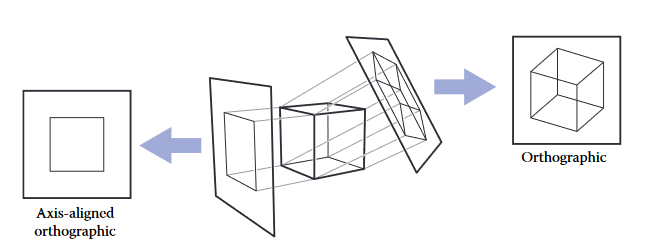
투영 방향과 이미지 평면을 어떻게 선택하느냐에 따라 시점이 결정됨.
이미지 평면이 시점 방향에 수직이라면 그 투영을 정사영 (orthographic)이라고 하고, 그 외의 경우 경사 투영 (oblique projection)이라고 함.
평행 투영은 평행선을 유지하고 이미지 평면에 평행한 평면 오브젝트의 크기 및 모양을 보존하기 때문에 기계 및 건축 도면에 많이 사용됨.
평행 투영의 장점은 동시에 단점이기도 함. 현실에서 물체는 멀어질수록 작게 보이며, 이 때문에 평행선이 거리가 멀어지면서 평행선처럼 보이지 않을 수 있음. 그 이유는 사람의 눈이 빛을 한 방향에서만 받지 않고 특정 뷰포인트를 통과하는 빛을 받기 때문임.
원근 투영 (perspective projection)을 사용하면 사람이 보는 것과 같은 시점을 만들 수 있음. 원근 투영이란 평행선이 아닌 한 점, 즉 뷰포인트 (viewpoint)를 지나는 직선을 따라 투영하는 것.
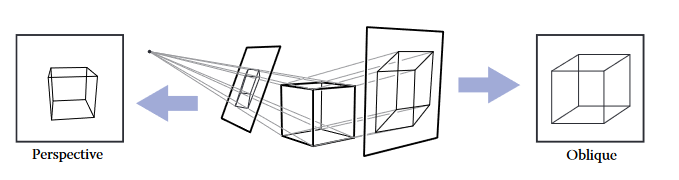
이 방식을 사용하면 뷰포인트에서 멀리 떨어진 물체는 투영되었을 때 자연스레 더 작아질 것. 시점은 뷰포인트와 이미지 평면을 무엇으로 선택하느냐에 따라 결정됨. 평행 투영에서와 마찬가지로 경사 (oblique) 및 비경사 (non-oblique) 시점이 존재함. 이미지 중심에서의 투영 방향에서 차이가 발생함.
3점 원근법 (three-point perspective)은 원근 시점을 수동으로 구성하기 위한 방식임.
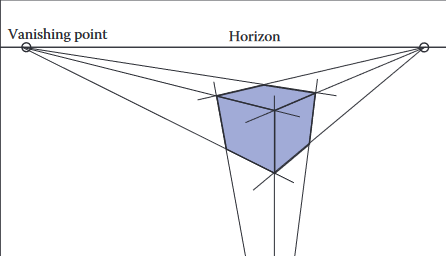
원근법의 놀라운 점은 간단한 수학적 규칙만 따른다면 원근법 규칙을 자동으로 적용할 수 있다는 점임. 물체는 눈을 향해 직접 투영되고, 눈 앞에 있는 시점 평면과 만나는 곳에 그릴 수 있음.
4.3. viewing ray 연산
광선 생성에 기본적으로 사용되는 도구는 뷰포인트와 이미지 평면임. 또한 카메라 기하학을 구체적으로 구현하기 위한 많은 방법이 존재함.
광선을 생성하기 위해 가장 먼저 해야 하는 것은 광선을 수학적으로 표현하는 것. 수학적인 관점에서 광선은 원점과 전파 방향을 가지며, 3차원 매개변수 직선이 이를 표현하기에 좋음. 사람의 눈 에서 이미지 평면 위의 점 까지의 3차원 매개변수 직선은 다음과 같음.
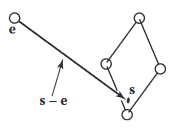
"에서 출발하여 벡터 를 따라 거리 비율 만큼 점 로 나아간다."
주어진 를 통해 점 를 결정할 수 있고, 점 를 광선의 원점, 벡터 를 광선의 방향이라고 함.
식에 대입해보면 알겠지만 임. 인 경우 은 보다 눈에 더 가깝다고 할 수 있음. 또한 인 경우 는 눈 뒤에 위치함.
눈 뒤에 있지 않은 광선에 가장 가까운 물체를 찾고자 할때 이러한 사실을 유용하게 사용할 수 있음.
viewing ray를 계산하기 위해 필요한 것은 와 임. 그중 는 언뜻 보면 찾기 어려울 수 있지만 적절한 좌표계를 사용한다면 쉽게 찾을 수 있음.
모든 광선 생성 메소드는 카메라 프레임 (camera frame)이라는 정규직교 좌표 프레임으로부터 시작함. 여기서 는 눈 또는 뷰포인트를 나타내며 는 기저 벡터로, 각각 는 오른쪽 (카메라 기준), 는 위쪽, 는 뒤쪽을 가리킴. 즉 는 오른손 좌표계를 형성함.
카메라 프레임을 구성하는 일반적인 방법은 뷰포인트 를 사용하는 것. 이때 뷰 디렉션 (view direction) 는 up 벡터로, 뷰 디렉션과 up 방향으로 정의된 평면에서 를 갖는 기저를 생성할 때 사용됨.
4.3.1. 정사영 뷰
정사영 뷰에서는 모든 광선이 방향 를 가짐. 평행 뷰는 자체적인 뷰포인트를 갖지 않지만 광선이 시작하는 평면을 정의하기 위해 카메라 프레임의 원점을 사용하여 물체가 카메라 뒤에 있어도 되게끔 함.
viewing ray는 점 와 벡터 로 정의된 평면에서 시작해야 하며, 알아야 하는 정보는 평면 위의 이미지가 있어야 하는 위치임.
앞으로 이미지 차원을 이미지의 네 변에 해당하는 4개의 숫자로 정의할 것. 은 각각 왼쪽, 오른쪽 변으로, 에서 시작하여 벡터 를 따라 측정됨. 는 각각 하단, 상단 변으로, 에서 시작하여 벡터 를 따라 측정됨. 일반적으로 임.
픽셀 크기의 이미지를 크기의 사각형에 맞추려면 픽셀들이 만큼 가로로, 만큼 세로로 위치해야 하며, 각 변의 반만큼의 공간이 이미지 사각형 내의 픽셀 그리드에 맞춰져야 함. 즉 래스터 이미지의 위치에 있는 픽셀은 다음과 같은 위치를 가짐.
- (1)
는 원점 와 기저 에 대해 측정된 이미지 평면 상의 픽셀 위치 좌표.
정사영 뷰에서 픽셀의 이미지 평면 위치를 광선의 시작점으로 사용할 수 있고, 광선의 방향은 뷰 디렉션과 같음.
정사영 뷰에서 viewing ray를 생성하는 과정은 다음과 같음.
식 (1)을 통해 를 계산한다.
ray.direction =
ray.origin =
경사 평행 뷰를 생성하기 위해서는 그냥 이미지 평면의 법선 를 뷰 디렉션 와 별도로 지정하면 됨. 위 과정과 똑같은 과정인데 만 로 바뀐 것.
4.3.2. 원근 뷰
원근 뷰의 경우 뷰포인트에서 모든 광선의 원점이 같음. 다만 방향은 픽셀마다 다름. 더이상 이미지 평면은 에 위치하지 않고 앞의 일정 거리 만큼에 위치함. 이 거리를 평면 거리 (plane distance), 혹은 좀 더 느슨하게 초점 길이 (focal length)라고 함. 초점 길이라고 하는 이유는 를 선택하는 과정이 카메라에서 초점의 길이를 맞추는 것과 같은 과정이기 때문.
각 광선의 방향은 뷰포인트와 이미지 평면 위에 있는 픽셀의 위치에 따라 정의됨. 이 과정이 위 그림에 나와있고, 다음과 같이 나타낼 수 있음.
식 (1)을 통해 를 계산한다.
ray.direction =
ray.origin =
평행 투영처럼 경사 원근 뷰는 이미지 평면의 법선을 투영 방향과 별도로 지정하여 생성할 수 있음. 위 식과의 차이는 를 로 바꾼 것 뿐.
4.4. 광선과 물체의 교점
광선 를 생성하고 나면 다음으로는 에서 물체와 만나는 첫 번째 교점을 찾음. 일반적으로 구간 사이의 에 따라 결정되는 표면과 광선이 만나는 첫 번째 교점을 찾는 식으로 진행함. ()
4.4.1. 광선과 구의 교점
광선 와 암시적 표면 이 주어졌을 때 이들이 어디서 만나는지를 알고자 함. 광선 위의 점들이 암시적 방정식을 만족하여 찾는 의 값이 방정식의 해가 될 때 교점을 구할 수 있음.
또는
중심점 와 반지름 을 갖는 구는 다음과 같이 나타낼 수 있음.
벡터 형식:
방정식을 만족하는 점 는 구 위에 존재함. 광선 위에 있는 점을 방정식에 대입하면 에 따른 방정식을 도출할 수 있음.
=
이 식에서 알고 있는 값들을 없애고 에 대한 이차방정식으로 표현하면 다음과 같음.
이 방정식의 해는 2.2에서 다뤘음.
를 판별식이라고 하는데, 이 판별식을 통해 실근의 개수를 알 수 있음.
판별식이 0보다 작은 경우 직선과 구는 만나지 않음.
판별식이 0보다 큰 경우 두 개의 해가 존재하는데, 하나는 광선이 구에 들어가면서 만나는 교점, 다른 하나는 광선이 구에서 빠져나오면서 만나는 교점. (즉, 교점이 2개지요)
판별식이 0인 경우 직선과 구는 접함. (교점이 1개)
위 방정식의 해를 자세히 표현하면 다음과 같음.
실제 구현 과정에서는 다른 부분을 계산하기 전에 판별식의 값을 먼저 체크해야 함. 만약 구가 다른 물체의 경계로 사용된다면 판별식만 사용하여 맞았는지 (hit)만 확인하면 됨. (Unity의 Sphere Collider)
2.5.4에서 다뤘던 것처럼 점 의 법선 벡터는 기울기 로 주어지고, 단위 법선은 임.
4.4.2. 광선과 삼각형의 교점
광선과 삼각형의 교점을 계산하기 위한 많은 알고리즘이 존재함. 질량 중심 좌표가 장기 스토리지를 사용하기 않기 때문에, 삼각형을 포함하는 매개변수 평면을 표현할 때 이를 사용함.
광선과 매개변수 표면이 만나기 위해 데카르트 좌표에 맞는 방정식을 설정해야 함.
또는
3개의 식과 3개의 미지수가 있기 때문에 이를 연립하여 방정식을 풀 수 있음.
매개변수 표면이 매개변수 평면인 경우 매개변수 방정식을 벡터 형태로 나타낼 수 있음. 삼각형의 각 정점이 일 때 교점의 방정식은 다음과 같음.
- (2)
교점 는 광선 위에 있을 것.
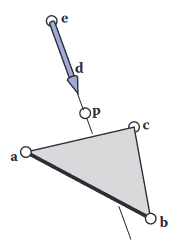
이면 교점은 삼각형 내부에 존재함. (역도 성립) 그렇지 않은 경우 광선은 삼각형을 빗나간 것. (교점이 외부에 위치)
방정식의 해가 존재하지 않는 경우 삼각형이 퇴화 (degenerate)했거나 광선이 삼각형을 포함하는 평면에 평행한 것.
방정식 (2)의 해 를 구하기 위해 이 식을 벡터 형태에서 3개의 연립방정식으로 바꿔야 함.
이는 또한 행렬방정식의 표준 형태로 나타낼 수 있음.
크래머 공식 (Cramer's rule)을 사용하여 위 방정식을 풀 수 있음.
이때 행렬 이고, 는 의 행렬식 (determinant)임.
선형적인 해가 필요한 광선과 삼각형 사이의 교점에 대한 알고리즘은 빠른 종료를 위한 조건이 필요함. 따라서 함수는 다음과 같이 작성되어야 함. (의사코드 (pseudocode)로 작성하였음)
boolean raytri(ray r, vector3 a, vector3 b, vector3 c, interval [t_0,t_1])
compute t
if (t < t_0) or (t > t_1) then
return false
compute γ
if (γ < 0) or (γ > 1) then
return false
compute β
if (β < 0) or (β > 1 - γ) then
return false
return true4.4.3. 광선과 다각형의 교점
개의 정점 을 갖는 다각형과 표면 법선 이 주어졌을 때, 광선 와 다각형을 포함하는 평면 사이의 교점을 암시적 방정식으로 표현하여 계산할 수 있음.
여기서 로 놓고 를 구하면
이를 통해 를 계산할 수 있음. 만약 가 다각형 내부에 있으면 광선이 다각형에 맞은 것.
점과 다각형의 각 정점을 평면에 투영하여 어떤 가 다각형 내부에 존재하는지 알아낼 수 있음. 점 에서 2차원 광선을 보내고 광선과 다각형 경계 사이의 교점의 개수를 측정하는 것이 쉬운 방법 중 하나임.
교점의 개수가 홀수인 경우 점은 다각형 내부에 있고, 짝수인 경우 외부에 있음. 그 이유는 광선의 특성으로 인해 다각형에 들어가면 반드시 나와야 하기 때문. (교점이 항상 2개) 반면 다각형 내부에서 출발하는 광선은 교점이 하나밖에 생기지 않음.
계산을 쉽게 하기 위해 2차원 광선은 x축을 따라 전파될 수 있음.
에 대해 와 같은 변과 광선의 교점을 계산하는 것이 직관적임.
하지만 다각형을 평면에 투영했을 때의 결과가 직선인 경우 문제가 생김. 이러한 문제를 피하기 위해서는 평면 중에서 가장 좋은 것이 무엇일지 선택해야 함. 인덱싱을 쓸 수 있도록 점을 구현하면 (ex. ) 다음과 같음.
if (abs(z_n) > abs(x_n)) and (abs(z_n) > abs(y_n)) then
index0 = 0
index1 = 1
else if (abs(y_n) > abs(x_n)) then
index0 = 0
index1 = 2
else
index0 = 1
index1 = 2이렇게 구현하고 나면 대신 p(index0)과 같은 표현을 쓸 수 있음.
4.4.4. 여러 물체의 교점
물론 대부분의 장면들은 하나 이상의 물체를 포함하고, 광선이 장면과 만날 때 카메라에 가장 가까운 교점을 찾아야 함. 이를 간단하게 구현하는 방법은 여러 물체들을 그냥 다른 타입의 물체로 생각하는 것임.
광선이 여러 물체와 만나면 그 물체 그룹에 있는 물체에 대해 교점을 값으로 반환할 수 있음.
hit = false
for each object o in the group do
if (o is hit at ray parameter t and t in [t_0, t_1]) then
hit = true
hitobject = o
t_1 = t
return hit4.5. 셰이딩
픽셀의 표면을 알아냈으면 픽셀값은 셰이딩 모델 (shading model)에 의해 계산됨. 이는 온전히 어플리케이션에 달린 일이며, 간단한 휴리스틱부터 매우 정교한 수치 계산까지 방법이 존재함.
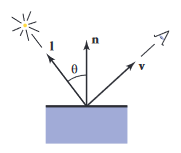
대부분의 셰이딩 모델은 빛 반사 과정을 표현하기 위해 설계되었으며, 이 때문에 표면은 광원에 의해 빛이 나고, 빛의 일부를 카메라에 반사함. 단순한 셰이딩 모델은 점광원 (point light source)의 조도로 정의됨. 빛 반사에서 중요한 변수는 빛의 방향 , 뷰 디렉션 , 표면 법선 임.
- 빛의 방향 : 광원을 가리키는 단위 벡터
- 뷰 디렉션 : 눈이나 카메라를 가리키는 단위 벡터
- 표면 법선 : 반사가 발생하는 점의 표면과 수직인 단위 벡터
이 외에도 특정 모델에 따라 색상, 광택 (shininess) 등의 특성이 존재함.
4.5.1. 람베르트 셰이딩
가장 간단한 셰이딩 모델은 18세기 스위스의 수학자 Johann Heinrich Lambert가 제시한 개념에 기반한 모델임. 개념에 따르면 표면의 한 영역에 떨어지는 광원의 에너지량은 표면과 빛 사이의 각도에 따라 달라짐. 빛을 수직으로 받는 표면의 경우 빛을 최대로 받고, 빛의 방향과 접하는 표면의 경우 빛을 받지 못함. 그 사이의 값은 표면 법선과 광원 사이의 각도 의 코사인 값에 비례함.
이러한 셰이딩 모델을 람베르트 셰이딩 모델이라고 함.
이때 은 픽셀 색상, 는 확산 계수 (diffuse coefficient) 또는 표면 색상, 는 광원의 세기임. 이 단위 벡터이기 때문에 을 를 쓰지 않고 편하고 짧게 쓸 수 있음. 이 방정식은 색상 채널 3개에 각각 적용됨.
벡터 은 광원의 위치에서 광선과 표면의 교점을 빼서 구할 수 있음. 단, 은 반드시 단위 벡터여야 함. 셰이딩 연산 과정에서 매우 흔하게 발생하는 오류가 벡터를 정규화하지 않는 것임.
4.5.2. Blinn-Phong 셰이딩
람베르트 셰이딩은 시점과 독립적임. 즉 표면의 색상은 바라보는 방향과 별개임. 하지만 실제 표면은 어느 정도 광택을 띄고 하이라이트 또는 정반사 (specular reflection)를 생성함. 이에 따라 바라보는 방향에 따라 보이는 모습이 조금씩 달라짐. 람베르트 셰이딩은 하이라이트를 만들지 못하고 광택이 없으며, 많은 셰이딩 모델들은 람베르트 셰이딩에 정반사를 추가함.
간단하고 specular highlight에 많이 사용되는 모델은 Bui Tuong Phong에 의해 제안되었으며, 추후 James F. Blinn (Jim Blinn)에 의해 오늘날 많이 쓰이는 형태로 업데이트되었음.
와 이 표면 법선을 가로질러 대칭적으로 위치할 때, 즉 거울 반사가 발생할 때 가장 밝은 반사가 생성되는 것이 아이디어. 벡터가 거울에서 멀어지면 반사는 부드럽게 줄어듦.
반벡터 (벡터 사이의 각을 이등분하는 벡터)를 표면 법선과 비교하면 거울 반사와 얼마나 비슷한지 확인할 수 있음.
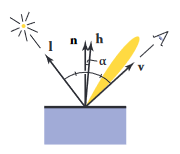
반벡터가 표면 법선 벡터와 가까우면 거울에 해당하는 요소가 밝아져야 하고, 반대로 멀어지면 어두워져야 함.
결과는 와 의 내적으로 얻어지고, 빠른 감소를 위해 를 지수로 사용할 수 있음. 이 지수, 즉 Phong 지수는 표면의 뚜렷한 광택을 조절함.
반벡터 자체는 계산하기 쉬움. 와 이 같은 길이를 갖기 때문에 두 벡터의 합은 사이각을 이등분하는 벡터이고, 를 생성하기 위해 정규화만 하면 됨.
이러한 개념을 모두 적용한 Blinn-Phong 셰이딩 모델은 다음과 같음.
는 표면의 스페큘러 계수 (specular coefficient) 또는 스페큘러 색상이라고 함.
4.5.3. 앰비언트 셰이딩
조명이 전혀 없는 표면은 완전히 검은색으로 렌더링됨. 검은 그림자를 피하기 위해 쓸 수 있는 조잡하지만 유용한 방법은 셰이딩 모델에 상수를 추가하는 것. 픽셀 색상의 정도는 표면 지오메트리에 전혀 의존하지 않고 오직 맞은 (hit) 물체에만 의존함. 이를 앰비언트 셰이딩 (ambient shading)이라고 하며, 어느 곳에서나 똑같이 들어오는 잔잔한 (ambient) 빛에 의해 표면이 빛나는 것과 같음.
매개변수 조작을 편하게 하기 위해 앰비언트 셰이딩은 주변 빛 색상에 따른 표면 색상의 곱으로 표현되어 개별적으로, 또는 모든 표면에 대해 조정할 수 있음.
Blinn-Phong 모델과 함께 앰비언트 셰이딩은 간단하고 유용한 셰이딩 모델임.
- (3)
는 표면의 앰비언트 계수 (ambient coefficient) 또는 앰비언트 색상, 는 앰비언트 빛의 세기를 나타냄.
4.5.4. 여러 점을 갖는 빛
빛의 좋은 특성 중 하나는 중첩 (superposition)으로, 하나 이상의 광원에 의해 발생하는 효과는 단순히 개별 광원으로 인해 발생하는 효과들의 합임. 이러한 이유로 앞서 다뤘던 셰이딩 모델은 개의 광원으로 확장할 수 있음.
- (4)
는 각각 강도, 방향, 번째 광원에 대한 반벡터임.
4.6. 레이트레이싱 프로그램
지금까지 주어진 픽셀에 대해 viewing ray를 생성하는 방법, 물체와 가장 가까운 교점을 찾는 방법, 이를 셰이딩하는 방법을 다뤘음. 이들은 모두 숨겨진 표면을 제거한 셰이딩 이미지를 생성하는 프로그램에 필요한 요소들임.
for 각 픽셀 do
viewing ray를 계산한다
if (광선이 t ∈ [0, ∞) 물체에 닿으면) then
n을 계산한다
셰이딩 모델을 평가하고 픽셀을 해당 색상으로 지정한다
else
픽샐 색상을 배경색으로 지정한다이때 "광선이 t ∈ [0, ∞) 물체에 닿으면" 부분은 4.4.4에 제시된 알고리즘을 통해 구현할 수 있음.
표면과의 교점을 구하는 루틴을 구현할 때에는 광선에 맞은 물체에 대한 참조를 리턴하거나, 적어도 법선 벡터와 셰이딩 관련 속성을 리턴해야 함. 이는 주로 정보에 대한 레코드나 자료구조로 구현함.
객체지향적인 구현에서는 surface와 같은 클래스를 만들고 triangle, sphere, group 등의 클래스가 이를 상속받도록 하는 것이 좋음. 광선이 닿을 수 있는 모든 물체는 surface를 상속받아야 함.
4.6.1. 레이트레이싱을 위한 객체지향 설계
레이트레이싱의 핵심적인 클래스는 모델을 구성하는 기하학적 물체임. 이들은 모두 어떤 기하학적인 물체 클래스의 서브클래스 (subclass)여야 하고, hit 함수를 제공해야 함.
기하학적인 "물체"와 프로그래밍에서의 "객체"가 같은 단어 (object)를 사용하므로 대부분 surface라는 클래스 이름을 사용함. 이러한 클래스를 사용하면 모델링의 최소 단위를 거의 고려하지 않고 일반적인 인터페이스를 제공하는 레이트레이싱을 구현할 수 있고, 오직 구만 사용하여 디버깅할 수 있음.
중요한 점은 광선에 닿을 수 있는 모든 것이 클래스 계층에 들어갈 수 있다는 것. 표면의 모음조차도 표면 클래스의 서브클래스가 될 수 있음. 바운딩 볼륨 계층 (bounding volume hierarchy)와 같은 구조도 광선에 닿을 수 있으므로 클래스에 들어감.
예를 들어, "추상" 또는 "기본" 클래스는 hit 함수와 bounding_box 함수를 정의함.
class surface
virtual bool hit(ray e+td, real t_0, real t_1, hit_record rec)
virtual box bounding_box()이때 은 hit이 리턴하는 광선 위의 구간이고, rec는 참조에 의해 전달 (pass by reference)되는 레코드이며, hit 함수가 true를 리턴할 때의 교점 와 같은 데이터를 포함함. box 자료형은 3차원 바운딩 박스 (bounding box)로, 표면을 감싸는 박스로 정의되는 두 점임. 예를 들어 구는 다음과 같이 구현할 수 있음.
box sphere::bounding_box()
vector3 min = center - vector3(radius, radius, radius)
vector3 max = center + vector3(radius, radius, radius)
return box(min, max)다른 클래스는 material임. material은 재료와 관련된 동작을 추상화하고 나중에 실제 머티리얼을 추가할 수 있음. 물체와 머티리얼을 연결하는 간단한 방법은 surface 클래스에서 material에 대한 포인터를 지정하는 것임.
4.7. 그림자
기본적인 레이트레이싱 프로그램을 만들었으면 그림자는 매우 쉽게 추가할 수 있음. 4.5에서 다뤘던 것처럼 빛은 특정 방향 로 진행함. 표면 위의 점 가 셰이딩되었다고 가정하면 방향에서 물체를 볼 경우 점 는 그림자 속에 있음. 물체가 없으면 빛은 차단되지 않음.
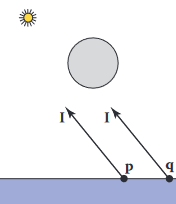
위 그림에서 광선 은 어떤 물체에도 닿지 않기 떄문에 점 는 그림자 속에 있지 않음. 반면 점 는 광선 이 물체에 닿기 때문에 그림자 속에 있음. 빛이 멀리 떨어져 있기 때문에 벡터 은 두 점에 상관 없이 동일함.
그림자 속에 있는지 없는지 결정하는 광선을 그림자 광선 (shadow ray)이라고 함. (viewing ray와 구분하기 위해 이름을 다르게 함)
셰이딩 알고리즘을 사용하기 위해 점이 그림자 속에 있는지 결정할 수 있는 if문을 추가해야 함. 일반적인 구현 과정에서 그림자 광선은 에 대해 체크하지만 수치 상의 부정확성 때문에 잘못하면 가 놓여있는 표면과의 교점을 체크할 수도 있음. 따라서 이러한 문제를 피하기 위해 이라는 매우 작은 양의 상수를 정의하여 에서 테스트함.
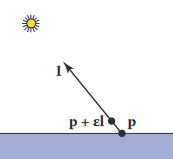
그림자 광선을 Phong 라이팅으로 구현하면 다음과 같음.
function raycolor(ray e+td, real t_0, real t_1)
hit_record rec, srec
if (scene->hit(e+td, t_0, t_1, rec)) then
p = e + (rec.t) * d
color c = rec.k_a * I_a
if (not scene->hit(p+sl, ε, ∞, srec)) then
vector h = normalized(normalized(l) + normalized(-d))
c = c + rec.k_d * I * max(0, rec, n ∙ l) + (rec.k_s) * I * (rec.n ∙ h)^rec.p
return c
else
return background_color앰비언트 색상은 가 그림자 속에 있는지 없는지에 따라 추가될 수 있음. 광원이 여러 개인 경우 각 빛마다 셰이딩 모델을 평가하기 전에 그림자 광선을 보낼 수 있음.
위 코드는 와 이 반드시 단위 벡터일 필요는 없다고 가정함.
4.8. 이상적인 정반사
레이트레이싱 프로그램에 이상적인 정반사, 또는 거울 반사를 추가하는 것은 그리 어렵지 않음.
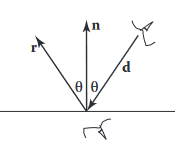
위 그림에서 방향 에서 보고 있는 사람은 표면에서 보이는 방향 의 물체를 볼 수 있음. Phong 빛 반사 방정식을 사용하여 벡터 을 구할 수 있음. 이 경우 는 표면을 가리키고 은 하늘을 가리키고 있기 때문에 다음과 같이 표현할 수 있음.
현실 세계에서는 빛이 표면에서 반사되면 해서 에너지가 어느 정도 손실되고, 이러한 손실은 색상마다 다름. 예를 들어, 금은 파란색보다 노란색을 효과적으로 반사하기 때문에 반사되는 물체의 색을 바꿈. 이러한 부분은 raycolor에서 재귀적인 호출을 추가하여 구현할 수 있음.
color c = c + k_m * raycolor(p+sr, ε, ∞)
이때 (거울 반사에서) 은 스페큘러 RGB 색상임. 그림자 광선에서와 마찬가지로 구간 을 지정해야 함. 물체에서 반사된 빛이 다시 물체를 맞추는 걸 원하지 않으니까.
다만 재귀적 호출을 사용하면 함수가 종료되지 않는 문제가 생길 수도 있음. 예를 들어 광선이 방 안에서 시작되는 경우, 방은 모든 면이 막혀 있으므로 광선은 무한히 반사될 것. 최대 재귀 횟수 (maximum recursion depth)를 지정하면 이러한 문제를 해결할 수 있음.
반사 광선이 이 0 (BLACK)이 아닌 경우에만 생성되도록 하면 코드를 더욱 효율적으로 짤 수 있음.
