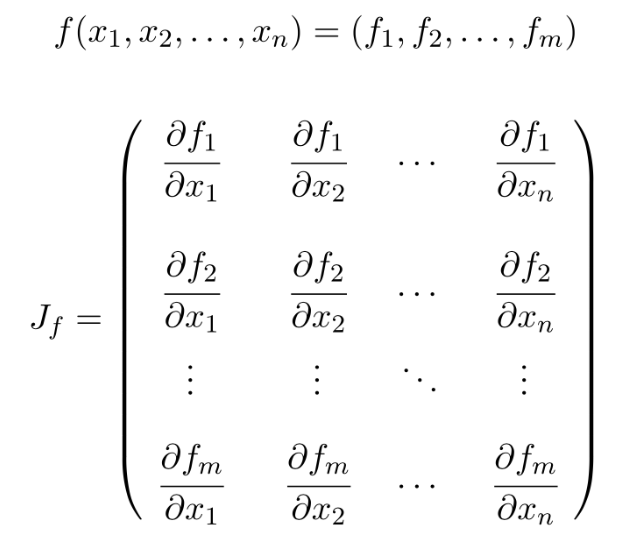1. Introduction
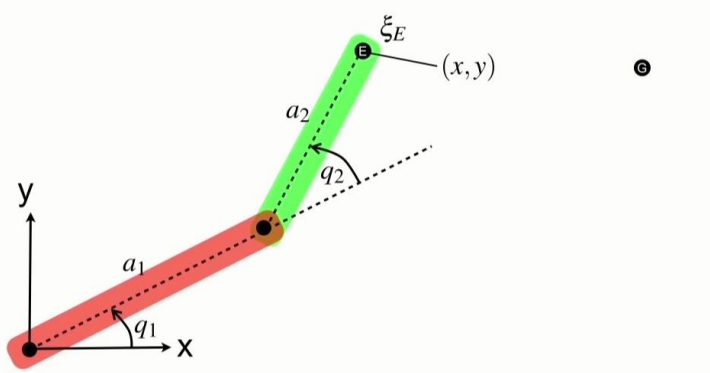
n개의 joint가 있고, θ1,⋯,θn에서 각 θj 값을 joint angle이라고 가정함. (j를 이용하여 θ 값을 순회함)
각 관절의 끝 부분을 end effector라고 함.
IK를 푼다는 것은 end effector가 최대한 target position과 가까워지도록 해를 찾아 자세를 만드는 것임.
몇 가지 정의 사항
- k : end effector의 개수. s1,⋯sk : 각 end-effector의 위치. 보통 root의 xyz 좌표계를 기준으로 정의함.
- end effector의 위치는 column vector (s1,s2,⋯sk)T로 정의하고, s라고 씀.
- target position 역시 column vector (t1,t2,⋯tk)T로 정의함. ti는 i번째 end effector가 닿아야 하는 target position
- joint angle 역시 column vector θ=(θ1,⋯,θn)T로 정의함.
- i번째 end effector의 desired change in position (얼만큼 변해야 하는지)는 ei=ti−si임. (ei : end effector의 변화, ti : target position, si : current position. goal - current)
- FK에서는 end effector position을 함수로 나타냄. s=f(θ) → 각도 θ가 주어졌을 때 end effector position이 어떻게 변해야 한다!
- 반대로 IK에서는 goal이 주어졌을 때 θ가 어떻게 되어야 하는지를 찾음. sd:θ=f−1(sd)
기억해야 할 것
- θ가 주어졌을 때 position이 얻어지는 건 FK, position이 주어졌을 때 θ가 구해지는 것은 IK
(FK : 어떻게 회전해야 저기로 손가락이 가지? vs IK : 손가락이 여기로 가려면 어떻게 회전해야 하지?)
IK를 하기 위해서는 “대략적으로 좋은 것”을 해야 함.
목표에 도달하는 방법의 가지수는 무한하기 때문에 해가 굉장히 많음. 따라서 많은 해 중에 최적의 해를 찾는 good approximation이 중요함.
- f() 함수는 non-linear operator임. → 해가 하나만 존재하지 않음.
- IK에는 “unreachable”, 즉 어떻게 해도 목표에 닿을 수 없는, 해가 존재하지 않는 경우가 있으며, 이 경우 최대한 목표를 향해 움직이려는 방향으로 해를 가정해야 함.
- 또한 가장 좋은 solution이 하나가 아닌 경우도 존재함.
⇒ IK가 non-linear operator인 이유
2. Kinetic Angular Variables [3]
기초 of 기초. 2d에서 시작해서 3d로 확장할 것임.
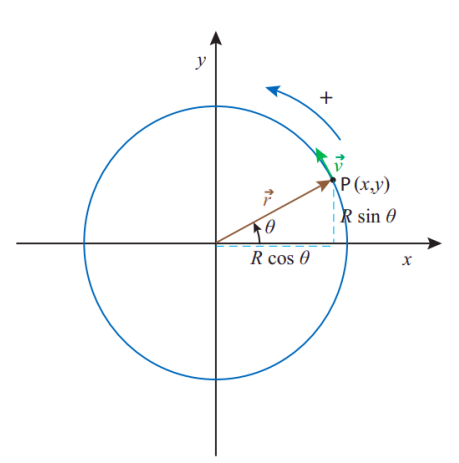
원 위에서 particle이 움직이고 있다고 가정함. 이때 particle의 좌표는 데카르트 좌표 (x,y)로 표현할 수 있음.
하지만 x,y만 주어졌다고 해서 점이 “얼마만큼의 속도로 얼만큼” 움직였는지는 알 수 없음. (직선을 따라 움직이는 점의 속도는 쉽게 구할 수 있지만, 원을 따라 움직이는 점의 속도는 쉽게 구할 수 없음)
이 때문에 원 위에서 점의 움직임을 표현하는 간단한 방법은 angle θ를 사용하여 단위 시간 t에 이 점이 몇 도만큼 회전했는지를 표현하는 것이 가장 직관적임.
여기서는 x축을 기준으로 회전한다고 가정하고, 반지름 R, 각 θ가 주어졌을 때 x,y는 간단하게 x=Rcosθ,y=Rsinθ로 표현할 수 있음. (ccw를 사용하기 때문에 반시계 방향으로 회전하는 것이 양수, 시계 방향은 음수)
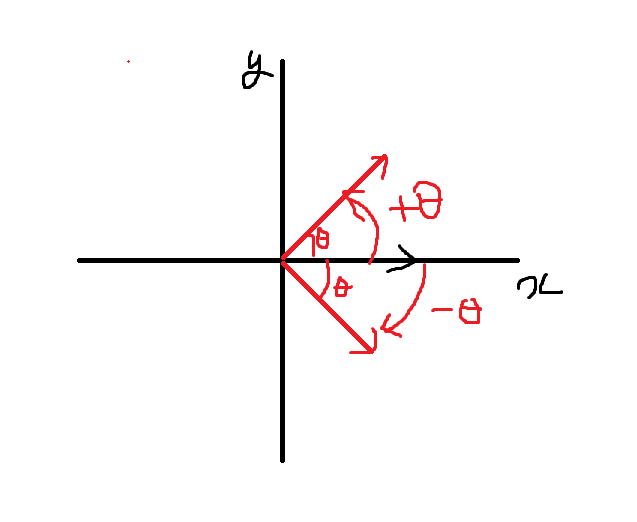
단위 시간 t에서 점이 움직이는 방향을 각속도 (angular velocity)라고 하며, ω로 표현함.
단위 시간 Δt 동안 움직인 각도를 Δθ=θ(t+Δt)−θ(t)로 정의함.
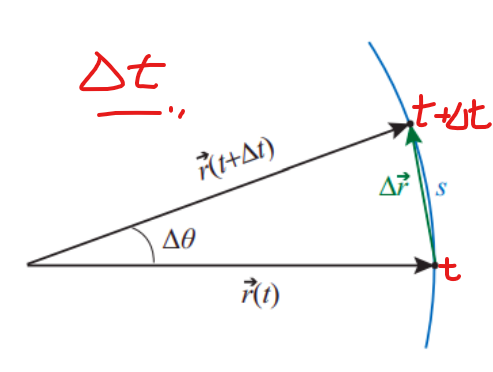
이때의 각속도 ω=limΔt→0ΔtΔθ=dtdθ (속도=거리/시간)
또한 θ(t)=θi+ω(t−ti) 또는 Δθ=ωΔt (θi는 초기 각도, t−ti는 시간 변화 → θi에서 출발하여 각속도 ω로 t−ti만큼 이동한 결과가 θ(t)인 것. 시간 x 속도 == 거리 (각))
각속도 ω는 시간에 따라 변화하므로 각가속도 α=limΔt→0ΔtΔω=dtdω
따라서 위 식과 비슷하게 ω(t)=ωi+α(t−ti) 또는 Δω=αΔt이고, 이를 θ에 대한 식으로 다시 쓰면
θ(t)=θi+ω(t−ti)+21α(t−ti)2 또는 Δθ=ωiΔt+21α(Δt)2
θ를 라디안으로 표현한다면 Δθ만큼 움직인 호의 길이 s=R∣Δθ∣임.
각의 변위가 매우 작은 경우 (Δθ→0) s≅∣Δr∣로 표현할 수 있고 (호의 길이가 직선의 길이와 동일해짐), s=R∣Δθ∣와 Δt→0을 이용하면 결과적으로 직선 속도 v는 다음과 같이 표현할 수 있음.
∣v∣=R∣ω∣
Angular velocity in two dimensions [4]

점 p가 회전하고 있는데 V라는 힘이 작용하고 있는 상황. 이 경우 V는 V⊥와 V∥로 나눠지고, 점 p가 회전하는 힘은 V⊥에 의해 결정됨. (V를 V⊥로 사영 projection한 만큼 힘이 분산됨)
(V∥은 원의 반지름 벡터와 평행한 힘이기 때문에 작용하지 않음)
위 그림에서 r : 원점 O와 점 P를 잇는 위치 벡터, 극좌표 (r,ϕ). 점 p에는 선속도 v=v∥+v⊥가 작용함. (반지름 벡터와 평행한 v∥, 수직인 v⊥)
이때 각속도 ω는 다음과 같음. (v∥은 각이 변하지 않으므로 고려하지 않고, v⊥만 고려함)
ω=dtdϕ=rv⊥=rvsin(θ) (v⊥=rω에서 넘어옴)
각속도는 게임의 여러 군데에서 사용됨. (탄막게임, 회전을 이용하는 게임 등)
Practice
Q. 길이 9r의 투석기가 있고, ω의 각속도로 수박을 던짐. 또 길이 r의 투석기가 있는데, 동일한 각속도 ω를 가짐.
이때, 길이 9r 투석기의 선속도 vlarge와 길이 r 투석기의 선속도 vsmall은 몇 배 차이가 나는가?
A. vlarge=Rω=9rω, vsmall=Rω=rω. 따라서 vlarge=9vsmall
Angular velocity in three dimensions
3차원에서는 회전각을 axis-angle로 표현함.
기존 euler rotation에는 큰 단점이 존재함. → x, y, z축 기준 회전만 가능하다는 것. 꼭 세 가지 축으로만 회전할 수 있는 것이 아닌데 x, y, z축으로 제한시켜버리면 직관적이지 않음. + 짐벌락 문제 등
→ 이러한 문제를 해결하고 임의의 벡터를 기준으로 회전할 수 있게 하기 위해 axis-angle을 사용함. (임의의 축 기준)
axis-angle은 두 가지를 기준으로 표현함.
- 어떤 벡터를 기준으로 회전할 것인지에 대한 기준 벡터 u
- 얼만큼 회전할 것인지에 대한 각도 θ
이를 기존 euler rotation으로 표현하려면 우선 x, y, z축으로 내려서 기준 축을 맞춘 다음 rotation, 원래대로 역변환하는 과정을 거쳐야 함. → 너무 복잡하고 비효율적
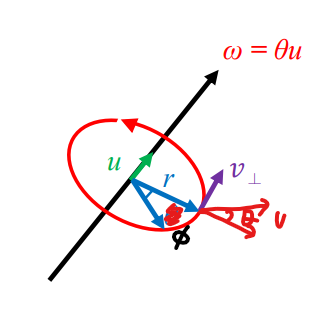
3차원 공간에서의 각속도 ω (orbital angular velocity)는 다음과 같음.
ω=ω2du=dtdθu=rvsin(θ)u (벡터 형태)
2d에서는 각속도를 quantity (10, 20 등과 같은 값)로 사용한 반면, 3d에서는 벡터로 사용하여 u 벡터에 곱해줌.
θ가 r과 v 사이의 각도이기 때문에 각속도 ω는 다음과 같이 다시 쓸 수 있음.
ω=rrrvsin(θ)u=r2r×v
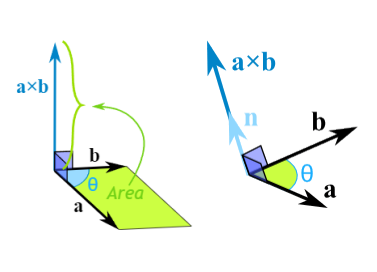
벡터 a, b가 있을 때, a×b의 크기는 두 벡터로 이루어진 평행사변형의 넓이 (quantity)임. 근데 여기에 벡터 n을 곱해주면 외적 벡터가 됨. 이 아이디어를 적용한 것이 위의 식. (r을 아래 위로 곱해준 이유)
즉, a×b=∣a∣∣b∣sin(θ)n이므로 이를 적용하여 다시 쓰면
ω×r=∣rvsin(θ)u∣∣r∣sin(90°)v^⊥=v⊥
중요한 공식 (많이 쓰게 됨)
(1) ω=r2r×v
(2) ω×r=v⊥ (2d에서는 ∣v∣=R∣ω∣)
3. Angular Momentum
Angular momentum and moment of inertia (각운동량 & 관성 모멘트) [5]
advanced한 개념. 물리적으로 올바르고 정확한 애니메이션을 구현할 때 사용되는 개념.
보통은 관절체를 다룰 때 특정 평면 위에서 다루는데, 이때 각운동량은 벡터의 형태로 다루어야 함.
하지만 IK와 같은 분야에서는 이를 스칼라의 형태로 다룰 수 있음. → why? 어떤 평면을 기준으로 회전할 것인지를 알고 있기 때문.
각운동량은 선운동량의 회전으로 생각할 수 있음. 즉, 선운동량 p는 질량 m과 선속도 v에 의해 p=mv의 형태로 정해짐.
이때 각운동량 L은 관성 I와 각속도 ω에 의해 L=Iω임. (회전체에서는 관성을 고려함)
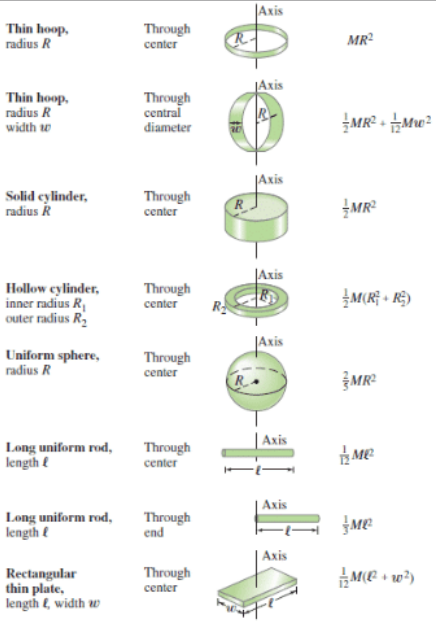
다양한 물체의 관성 값 → 가장 많이 쓰이는건 long uniform rod→through end
관성 모멘트는 속도를 갖고 움직이는 물체를 변화시킬 때 관성에 대한 저항을 I로 표현한 것. I가 클수록 변화하는데 작용하는 힘이 커짐.
관성 모멘트는 “질량이 회전축에 대해 어느 정도로 분포되어 있는지”에 따라 달라지는데, 보통은 모든 질량이 균일하게 분포하고 있다고 가정함.
4. Jacobian Inverse Methods
4-1. Problem defined by Jacobian
Jacobian J는 end effector s에 대한 모든 체인 시스템에 편미분을 수행한 행렬임.
linear transform은 수식화할 수 있고 비교적 직관적이고 간단함. 근데 non-linear transform이라면?
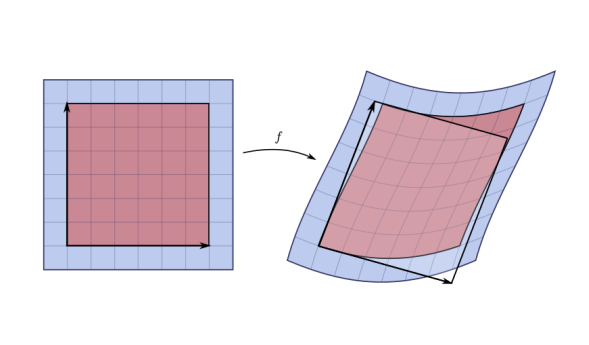
하나의 수식으로 표현하기 힘들 뿐더러 규칙도 발견되지 않아 어려움. → 이러한 non-linear transform에 사용되는 것이 jacobian
jacobian을 사용하면 도형을 잘게 쪼갤 수 있고, 잘게 쪼갠 곳에서 보면 마치 linear function인 것처럼 보이게 됨.
non-linear function을 linear function으로 근사하는 방식
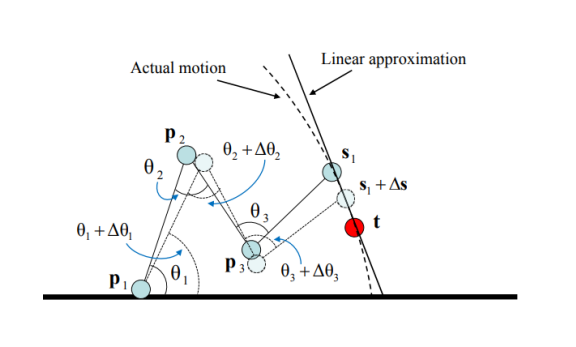
위 그림에서 실제 모션은 곡선 형태의 움직임. but 이를 국소적인 형태로 보면 (Δs가 매우 작음) 모션을 곡선 형태로 정의하나 직선 형태로 정의하나 큰 차이가 없음. → linear function으로 계산 가능
Jacobian J는 θ 값에 대한 함수임.
J(θ)ij=(∂θj∂si)ij (i=1,⋯,k, j=1,⋯,n) → i는 end effector를 순회할 때 사용하는 변수, j는 joint들을 순회할 때 사용하는 변수임.
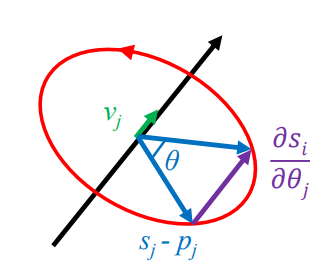
∂θj∂si=vj×(si−pj) [1]
→ si는 end effector의 위치. θj는 joint angle이므로 위치 / 각도 == 각속도임. 따라서 위와 같은 식이 나오는 것.
(vj : 회전하고자 하는 축의 unit vector, si : end effector의 위치, pj : joint의 현재 위치)
forward dynamics에서는 s=f(θ)임. 따라서 이렇게 쓸 수 있음. → dttds=J(θ)dttdθ (이때 J(θ)=dθds, tt : 시간) (양변을 시간에 대해 미분한 결과)
FK에서는 θ,s,t를 모두 알고 있기 때문에 jacobian J=J(θ)를 계산할 수 있음.
즉 end effector의 위치 변화는 Δθ만큼 업데이트했을 때 Δs≈JΔθ임. (위 식과 동일)
IK의 목표는 Δs가 desired position e=t−s와 최대한 같아지게 만드는 것.
따라서 FK는 e=JΔθ를 푸는 것이고, IK는 Δθ=J−1e를 푸는 것임.
4-2. Jacobian Pseudo-inverse
역행렬을 구하는 것이 그렇게 쉽지는 않음. → 행렬의 크기가 커질수록, 또 정사각행렬이 아닌 경우 역행렬 구하기는 훨씬 어려워짐.
→ Jacobian이 정사각행렬이 아니거나 역행렬이 존재하지 않는 경우가 있음.
역행렬이 존재하더라도 singular problem이 발생할 수 있음. (아무리 변화를 시켜도 도달할 수 없는 목표가 있음 → unreachable)
이를 해결하기 위해 Jacobian Pseudo-inverse (J+)를 정의함. → 반드시 inverse가 나오는 대신, 정확한 inverse가 아니라 근사치를 찾는 것. (따라서 JJ+≒I)
- 장점 : inverse가 무조건 나온다.
- 단점 : 정확하지 않다.
⇒ 하지만 정확하지 않더라도 해를 구할 수 있기만 하면 되기 때문에 IK에서는 Jacobian pseudo-inverse를 사용함.
J+는 방정식 e=JΔθ를 “least square” 방식으로 푸는 것임.
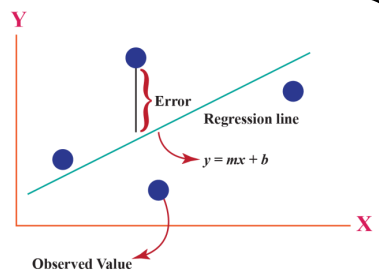
least square?
여러 데이터의 집합에서 “오차가 가장 적은” best fit을 찾는 것. 직선의 형태에서 출발하여 2, 3차 함수 등 곡선의 형태로 발전하여 오차를 줄이게 됨.
null space of a matrix
여러 속성 사이의 선형 관계를 정의하기 위해 사용되는 개념. 행렬 A,B에 대해 AB=0일 때, 행렬 A의 null space는 항상 zero vector를 포함함. → A0=0
행렬 (I−J+J)는 J의 null space로 projection을 수행한다. → I−J+J=0이 되도록 하는 J+를 찾는 것이 pseudo-inverse인 것.
따라서 모든 벡터 ψ에 대해 J(I−J+J)ψ=0이 성립함. Δθ=J+e+(I−J+J)ψ → IK의 방정식 Δθ=J−1Δθ에 더해 (I−J+J)ψ가 0이 되는 값을 찾는 것. (0으로 수렴하기 때문에 약간의 에러 값이 추가됨 → 어쨌든 IK를 풀 수 있는 상태가 됨.)
에러 JΔθ−e를 최소화하는 방향으로 문제를 품. (약간의 에러는 있을 수 있지만 어쨋든 해를 구할 수 있는 상태를 만드는 것이 목표임 → 이 정도 에러는 눈으로 구별되지 않음.) → optimization problem
Practice
Q. u=(u,v), p=(p,q), x=(x,y)일 때, T(u)=x이고, T(u,v)=(u2−v2,2uv)임.
- u(t)=(t,t2)의 t=1에서의 속도는?
- T(u,v)의 Jacobian을 구하라.
A.
- u′(t)=(1,2t)이므로 t=1에서의 속도는 (1,2)
- JT=[∂u∂T1∂u∂T2∂v∂T1∂v∂T2]=[2u2v−2v2u]
Jacobian matrix의 정의
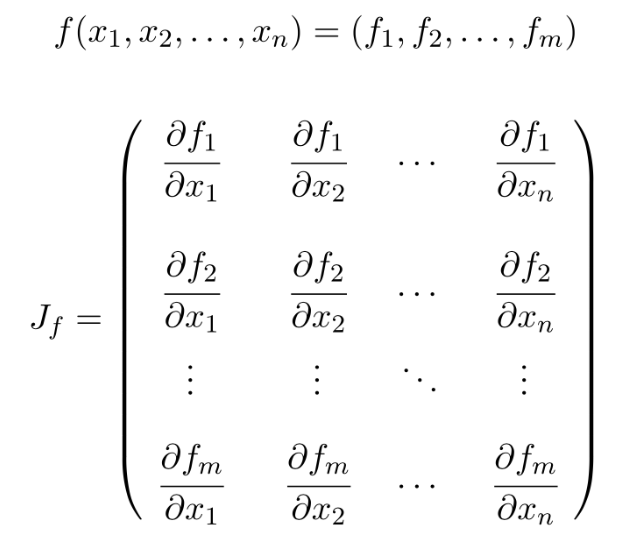
5. Singular value decomposition
5-1. SVD Introduction
SVD는 팔방미인 → 딥러닝, optimization, pseudo-inverse 등등에 많이 쓰임
SVD는 eigen decomposition & polar decomposition과 관련이 깊음.
행렬의 SVD는 “3개의 행렬로 쪼개는 것”이라고 볼 수 있음. ex) A=BCD
그 중 가운데 행렬, 즉 C에 singular value가 들어가기 때문에 singular value decomposition이라고 부름.
행렬 A에 벡터 x를 곱해서 새로운 행렬 Ax를 만든다고 가정. (변환을 수행할 때 벡터에 행렬을 곱하는 것과 마찬가지)
- [A]ij or aij는 행렬 A에서 “row i와 column j에 있는” 값을 의미함. (a11,a22 등)
- 벡터는 크기와 방향을 가지고 있음.
- 벡터에 행렬을 곱한다는 것은 “그 벡터에 회전 또는 길이 변화 (stretching)”를 수행한다는 의미임. (affine transform 참고)
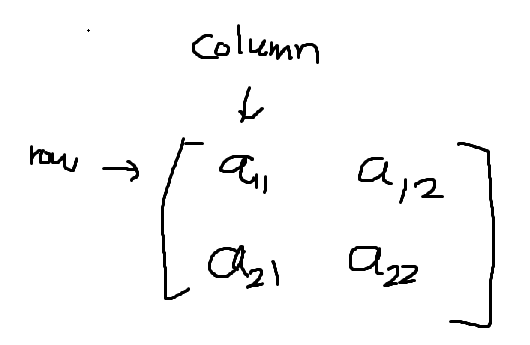
matrix factorization (decomposition)
행렬을 쪼개서 원하는 형태로 만드는 것. LU 분해, QR 분해 등 여러 가지 종류의 decomposition이 있음.
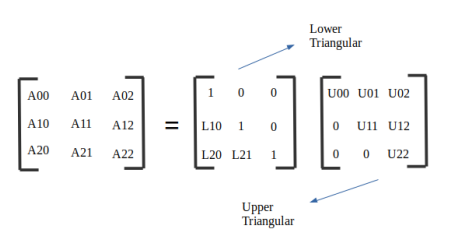
5-2. Transpose (전치행렬)
column vector ↔ row vector로 서로 바꾸는 행위. i-th row & j-th column 행렬을 j-th row & i-th column 행렬로 바꾸는 행위
ex) [AT]ij=[A]ji
ex) C=⎣⎢⎡135246⎦⎥⎤ → CT=[123456]
(AT)T=A임.
중요한 특징 → (AB)T=BTAT (순서 뒤집혀서 나옴)
또다른 중요한 특징
행렬이 실수가 아닌 경우 ([1−2j3+i]) → transpose를 취하면 conjugate (켤레복소수)가 됨. (A∗는 복소수 행렬에 대한 transpose)
[1−2j3+i]T=[1−2j3+i]∗=[1+2j3−i]
5-3. Partitioned Matrix
행렬 B=[123456]이 있을 때, 이를 column matrix로 나타내면 B=[u1u2u3]가 됨. → u1=[12],u2=[34],u3=[56] 또는 u1T=[12],u2T=[34],u3T=[56]
따라서 BT=⎣⎢⎡135246⎦⎥⎤, B=⎣⎢⎡u1Tu2Tu3T⎦⎥⎤
행렬을 B=u1x+u2y+u3z와 같이 나눠서 쓸 때 partitioned matrix를 사용함.
5-4. Eigenvalues & Eigenvectors
어떤 벡터의 방향을 바꾸지 않고 크기만 바꾸고 싶은 경우 스칼라 값을 곱하면 됨.
- 벡터 u와 스칼라 값 λ가 있을 때, 벡터 λu는 u와 방향은 같지만 크기가 다른 벡터임.
- 이때 행렬 A의 eigenvector는 Au=λu를 만족하는 non-zero vector u를 말하고, λ를 eigenvalue라고 함.
- ex) 행렬 B=[−101−2]가 있고, eigenvector u1=[10], u2=[−11]일 때, 각각의 eigenvalue는?
→ Bu1=λ1u1, Bu2=λ2u2
[−101−2][10]=[−10]=λ1[10] → λ1=−1
[−101−2][−11]=[2−2]=λ2[−11] → λ2=−2
하지만 실전에서는 행렬만 주어지고 eigenvector와 eigenvalue를 구하라고 함. (식은 1개, 미지수는 2개 ㄷㄷ) → 구하는 방법이 있긴 한데, 노가다임. (여기서는 다루지 않음. 컴퓨터가 알아서 계산해 주겠지 뭐)
실전에서는 getEigenVector(), getEigenValue()
5-5. Eigen Decomposition of a matrix [6]
행렬 A를 eigenvalue와 eigenvector로 분해하는 것은 “행렬 대각화”의 일종임.
SVD는 eigen decomposition의 한 종류임. (eigen decomposition > SVD)
A를 eigenvalue λ1,λ2,⋯,λk와 eigenvector X1,X2,⋯,Xk로 나눌 수 있다고 가정하면 다음과 같이 쓸 수 있음
⎣⎢⎢⎢⎢⎡x11x12⋮x1k⎦⎥⎥⎥⎥⎤,⎣⎢⎢⎢⎢⎡x21x22⋮x2k⎦⎥⎥⎥⎥⎤,⋯,⎣⎢⎢⎢⎢⎡xk1xk2⋮xkk⎦⎥⎥⎥⎥⎤
행렬 P가 다음과 같이 eigenvector로 이루어진 행렬과 eigenvalue로 이루어진 행렬 D로 분해된다고 정의함.
P=[X1X2⋯Xk]=⎣⎢⎢⎢⎢⎡x11x12⋮x1kx21x22⋮x2k⋯⋯⋱⋯xk1xk2⋮xkk⎦⎥⎥⎥⎥⎤ (column vector로 나눈 것)
D=⎣⎢⎢⎢⎢⎡λ10⋮00λ2⋮0⋯⋯⋱⋯00⋮λk⎦⎥⎥⎥⎥⎤
위에 나온 식 Au=λu를 적용하면 다음과 같이 쓸 수 있음.
AP=A[X1X2⋯Xk]
=[AX1AX2⋯AXk]
=[λ1X1λ2X2⋯λkXk]

=PD
⇒ ⭐AP=PD⭐
AP=PD에서 A만 남기고 우항으로 넘기면 A=PDP−1이 됨. → eigen decomposition의 결과
여기서 D가 eigenvalue로 이루어진 대각행렬이기 때문에 “행렬 대각화”라는 말을 쓴 것.
제약 조건 → A는 항상 정사각행렬이어야 함.
특징)
A2=(PDP−1)(PDP−1)=PD(P−1P)DP−1=PD2P−1 (D만 변화함) → (일반화) An=PDnP−1
역행렬도 마찬가지 → A−1=(PDP−1)−1=PD−1P−1
이때 D−1=⎣⎢⎢⎢⎢⎡λ1−10⋮00λ2−1⋮0⋯⋯⋱⋯00⋮λk−1⎦⎥⎥⎥⎥⎤ → λ1,λ2,⋯,λk의 역수
TIP) 직교행렬인 경우 P−1=PT
(실수에서 정의된 경우에만) PTP=I
Practice
Q. A=[3112]이고, eigenvector u1=[0.85070.5257], u2=[−0.52570.8507]임. eigenvalue가 λ1=3.618, λ2=1.382일 때, A=PDPT=?
A. [0.85070.5257−0.52570.8507][3.618001.382][0.8507−0.52570.52570.8507]
5-6. Singular value
행렬 A에 대해 ATA는 무조건 정사각행렬이 됨. (ex. 3x2 행렬의 경우 전치행렬은 2x3 → 곱하면 3x3 행렬이 됨) 또한 A의 모든 값이 실수라면 eigenvalue 역시 실수임.
이때 ATA의 eigenvalue의 square root ()를 singular value라고 함. → λ
5-7. Rank
행렬 A의 rank (계수) → 행렬 A의 column vector로 나타낼 수 있는 벡터 공간의 수
만약 같은 차원을 나타내는 벡터가 있다면 하나로 취급함.
ex)
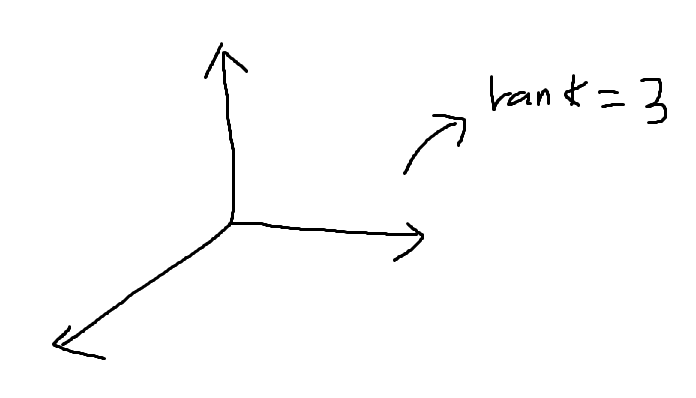
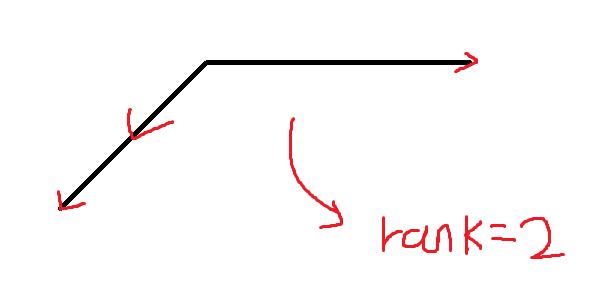
따라서 행렬 A의 선형 독립인 최대 column 개수가 rank가 됨.
행렬에서 같은 차원을 나타내는 최대 column 개수가 rank와 동일한 경우 full rank라고 함. 아닌 경우 rank-deficient
ex)
행렬 ⎣⎢⎡1−230−33110⎦⎥⎤의 rank == 2
첫 번째 column과 두 번째 column은 선형 독립, but (첫 번째 column) - (두 번째 column) = ⎣⎢⎡110⎦⎥⎤이므로 세 번째 column을 정의할 수 있음. 따라서 선형 독립 X
선형 독립?
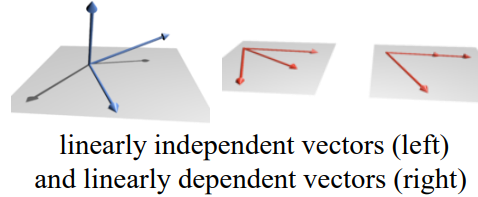
위 그림의 경우 세 벡터가 모두 다른 평면에 존재하여 다른 두 벡터로 한 벡터를 표현할 수 없을 때 선형 독립이라고 하고,
같은 평면에 있는 벡터가 존재하여 두 벡터로 한 벡터를 표현할 수 있을 때 선형 독립이 아님.
왼쪽 → 3차원, rank = 3 / 오른쪽 → 2차원, rank = 2
Practice
Q. A=[1−11−1002−2]의 rank는?
A. column vector [1−1]이 첫 번째, 두 번째 column에서 서로 같으므로 rank 1, [00]은 원점이므로 rank가 늘어나지 않음. [2−2]는 [1−1]를 2배하여 표현할 수 있으므로 같은 차원에 있음. 따라서 rank = 1
5-8. Singular value decomposition (SVD)
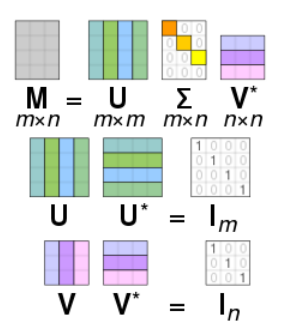
m×n 행렬 A의 SVD는 A=U∑V∗로 표현할 수 있음.
- U : m×m complex unitary matrix (U∗U=I)
- ∑ : m×n (eigen decomposition과 달리 정사각행렬이 아니어도 됨) 행렬. 대각선에 음수가 아닌 실수가 있음.
- V : n×n complex unitary matrix (V∗V=I)
A가 실수 행렬인 경우 U,V는 실수 공간에서의 직교 행렬임. 따라서 U∑VT로 표현 가능
- 대각선에 있는 값 σi=∑ii는 행렬 A의 singular value임. (ATA의 eigenvalue)
- 0이 아닌 singular value의 수 == A의 rank
- U의 column을 A의 left-singular vector, V의 column을 A의 right-singular vector라고 함.
- 이들은 각각 직교 기저 u1,⋯,um과 v1,⋯,vn을 구성함.
5-9. Geometric meaning of SVD
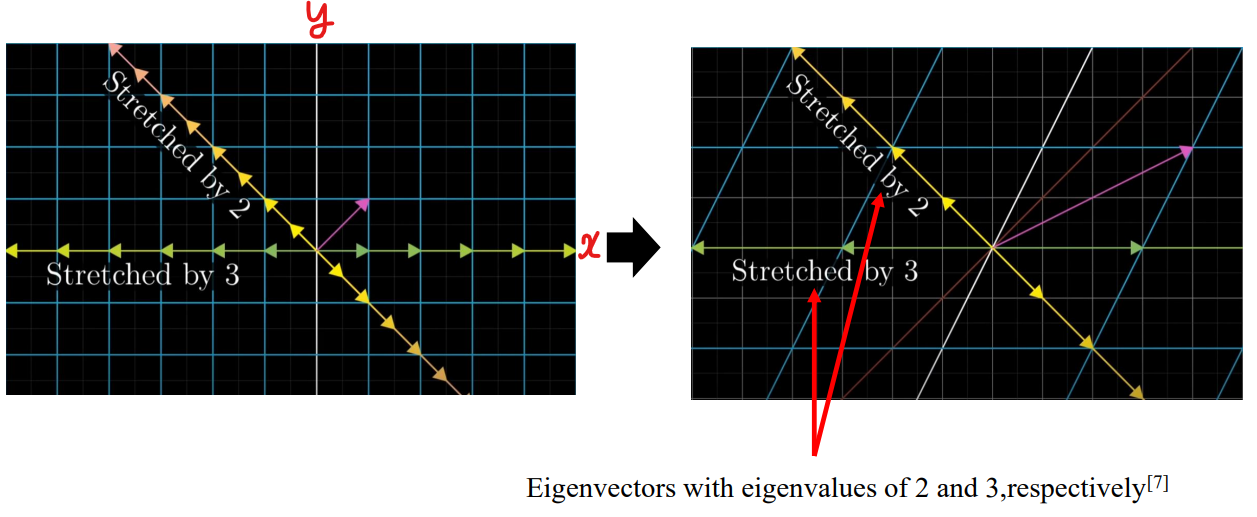
- eigenvector는 transform을 통해 어떤 벡터, 혹은 좌표계 자체를 “어떻게" 늘릴 (stretching) 것인지에 대한 의미. (방향 등)
- eigenvalue는 “얼만큼” 늘릴 것인지에 대한 것.
- eigenvector는 확대/축소를 해도 span (시점과 종점을 이은 공간)을 벗어나지 않음.
(참고)
(이미지를 클릭하면 영상이 재생됩니다)
SVD의 기하학적 의미
A=U∑V∗인데, 이는 곧 벡터에 대한 A라는 변환을 V∗ → ∑ → U라는 3가지 단계로 나누겠다는 의미.

T:Kn→Km이라는 선형 변환이 있음.
이때 linear map (A 행렬에 의해 수행됨)은 Rn의 원을 Rm의 타원으로 바꾸는 것을 의미함.
0이 아닌 singular value는 변화한 타원의 장축/단축을 의미함. (얼마만큼 stretch)
→ 복잡한 변환을 3개의 덜 복잡한 변환으로 나누어 생각하는 것이 SVD
5-10. SVD calculation (A=U∑VT)
- V의 column은 ATA의 eigenvector와 같음 (row vector)
- U의 column은 AAT의 eigenvector와 같음 (column vector)
- AAT,ATA의 eigenvalue를 각각 square root하여 나열한 것이 ∑
5-11. SVD example (A=U∑VT)

Reference
[1] Efficient computation of the jacobian for robot manipulators, 1984
[2] https://www.cuemath.com/data/least-squares/
[3] Motion on a Circle (Or Part of a Circle). (2020, November 6). University of Arkansas. (https://phys.libretexts.org/@go/page/22249)
[4] https://en.wikipedia.org/wiki/Angular_velocity
[5] https://en.wikipedia.org/wiki/Angular_momentum
[6] https://mathworld.wolfram.com/EigenDecomposition.html
[7] https://www.youtube.com/watch?v=PFDu9oVAE-g