
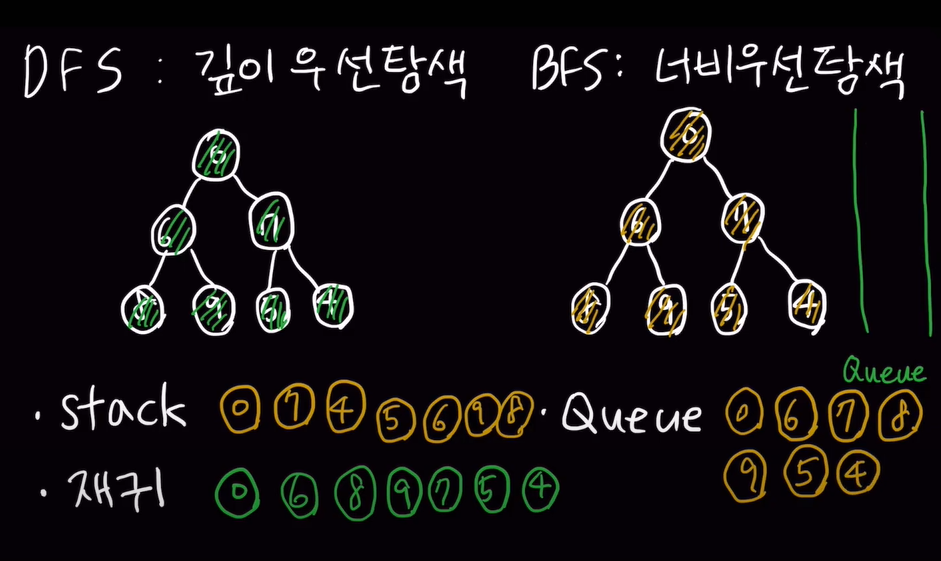
DFS / BFS를 따지면 드라마에 비유 할 수 있음
한 드라마가 종영 될 때까지 기다렸다가 한번에 본다 -> DFS
여러 드라마를 한편씩 업로드 마다 챙겨본다 -> BFS
대표적으로 이러한 그래프 관련 문제들은
- 경로 탐색 (최단거리, 시간)
- 네트워크 (연결)
- 조합 (모든 조합 찾기)
그렇기에 여행 경로, 단어 변환, 네트워크, 타겟넘버 등의 문제를 보면 아 이 알고리즘이구나를 떠올리면 좋음
꿀팁
DFS (stack)
-> 재귀 (한놈만 패니까)
대표 문제 유형
1. 경로 탐색 및 조합 문제
- N-Queen
- 순열 및 조합 생성
- 타겟 넘버
2. 그래프의 모든 경로 탐색
- 모든 경로 출력
- 미로 탐색
3. 백트래킹 문제
- 스도쿠
- 문자열 생성
(재귀로 여러 케이스를 다 준다음, 한 케이스를 빠져 나오면 (ex, 덧셈 뺄셈) 그 다음 케이스를 준비하여 모든 케이스를 파악, 모든 경로를 살피는데 적합하고 백트래킹과 함께 사용함)
BFS (queue)
-> Queue / LinkedList (여러놈 패니까)
대표 문제 유형
1. 최단 경로 문제
- 미로의 최단 경로
- 그래프의 최단 경로
- 이진 트리 레벨 탐색
2. 최소 이동 횟수 문제
- 말의 이동
- 게임 맵 최단거리
3. 레벨 기반 탐색
- 사회적 네트워크
- 조직도 탐색
(연결한다고 생각하면 됨, 가장 먼저 넣고 넣은 애와 연결된 걸 찾고 Queue가 빌 때까지 계속 반복, 큐를 사용해 넓게 탐색, 최단 거리 계산에 적합, 레벨별로 탐색하는데 유리)
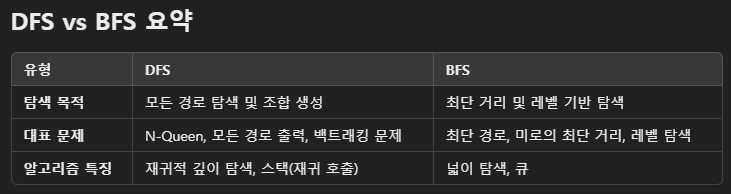
Q. 어떤 걸 써야하나요?
그냥 자기에게 맞는 걸 하면 됨. 두 알고리즘 중 아무거나 사용하더라도 문제는 풀리기 때문
DFS는 하나의 조합을 완성해서 정답과 비교하고 또 다른 조합을 만들어서 정답과 비교하는 방식이라 내가 검증하기 쉬움
하지만 BFS도 필요할 때도 있음 DFS는 한 놈이 너무 깊으면 안 되기 때문에 모든 조합에서 시간을 끌어버리기 때문
BFS는 한 정답을 찾으면 그 정답을 적용하기 쉬워서 시간 복잡도가 낮음
경로탐색, 네트워크, 조합 만들기 => DFS, BFS
(Lv.2) 타겟 넘버 (DFS)
DFS의 대명사라 해도 되는 문제라고 생각되는 문제
예전에 풀었던 기록이 새록하지만 다시 꼼꼼히 해설해보았음
function solution(numbers, target) {
let count = 0;
const dfs = (index, currentSum) => {
console.log(`DFS 호출: index = ${index}, currentSum = ${currentSum}`); // 현재 상태 출력
// 모든 숫자를 탐색한 경우에 target값과 맞는지 비교
// ! 애초에 if문에 만족하지 않으면 return을 만나지 않고 다시 함수 재실행
// ! index가 5 (4+1)라는 것은 모든 인덱스를 다 탐색했다는 것
// ! 즉, 인덱스를 다 탐색했을 때 과연 target과 맞냐는 확인
// 함수에서 return을 만나면 그 함수는 종료
// 하지만 중요한 점은 해당 함수 호출이 종료될 뿐, 그 함수가 호출된 이전 상태로 돌아가서 다음 작업이 진행
if (index === numbers.length) {
if (currentSum === target) {
console.log(`🎯 조건 만족: currentSum(${currentSum}) === target(${target})`);
count++;
} else {
console.log(`❌ 조건 불만족: currentSum(${currentSum}) !== target(${target})`);
}
return; // 탐색 종료
}
// ! 더하기를 진행하다 return을 만나면 불렀던 더한 경우는 종료, 뺀 경우가 진행
// 숫자를 더한 경우
dfs(index + 1, currentSum + numbers[index]);
// ! 더하기를 다 진행 후 - 빼기도 진행하다가 끝난 경우에도 바로 더하기를 진행
// 숫자를 뺀 경우
dfs(index + 1, currentSum - numbers[index]);
}
dfs(0, 0); // 초기 상태에서 탐색 시작
return count;
}
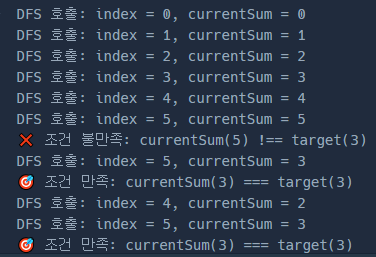
DFS는 정말 재귀만을 생각하고 풀면 됨
유의해야할 것은 어떤 경우에 조건문 탈 것이고 건너 뛸 것인지에 대해 유념해야 한다는 것
조건문을 타지 않아도 다시 한번 더 더하기가 진행될 것이고
빼기가 진행되더라도 마치면 다시 더하기가 한번 더 진행된다는 걸 유념해야함
또한, 더하기, 뺴기의 경우임을 인덱스를 조절해서 더하고 뺴는 것을 원할하게 해야함
다른 사람의 풀이
가장 깔끔하고 명확한 코드가 있어서 가져와봤음
function solution(numbers, target) {
let answer = 0;
getAnswer(0,0);
function getAnswer(x,value) {
if(x<numbers.length){
getAnswer(x+1,value + numbers[x]);
getAnswer(x+1,value - numbers[x]);
} else{
if(value === target){
answer++
}
}
}
return answer;
}
댓글 중에는 한 노드에서 두 노드로 뻗쳐나가는 것 같다고 했는데 그 말이 맞다고 생각될 정도로 깔끔하다!
(Lv.2) 게임 맵 최단거리 (BFS)
BFS의 대명사 문제
let dx = [-1, 0, 1, 0]
let dy = [0, 1, 0, -1]로 방향을 설정한 다음 visited를 채우던 문제, 오랜만에 봤지만 사알짝 떠오르던 문제였음
하지만 여기에서 유의해야할 것은 dx(row)이므로 세로방향으로 이동
ex) maps[0][1] -> maps[1][1]로 이동이라면 dx가 1증가 즉, 아래로 하나이동한 거기 때문에 그 점만 유의하면 괜찮음
function solution(maps) {
let ans = 1; // 이동 횟수 (출발지 포함)
let n = maps[0].length; // 지도 가로 길이
let m = maps.length; // 지도 세로 길이
let dx = [-1, 0, 1, 0]; // 상, 우, 하, 좌 방향
let dy = [0, 1, 0, -1];
let visited = []; // 방문 여부를 기록할 배열
for (let i = 0; i < m; i++) visited.push(new Array(n).fill(false));
visited[0][0] = true; // 시작점 방문 처리
let queue = []; // BFS를 위한 큐
queue.push([0, 0]); // 시작점을 큐에 추가
while (queue.length) {
let [x, y] = queue.shift(); // 큐에서 현재 위치를 가져옴
for (let i = 0; i < 4; i++) {
// 이동 후의 x 좌표
let nx = x + dx[i];
// 이동 후의 y 좌표
let ny = y + dy[i];
// ex. 여기에서 처음에 x가 0이고 dx[0] = -1이 들어가면 nx는 -1이므로 아래를 벗어남
// 조건 1. 지도 범위를 벗어나지 않고 (nx >= 0 && nx < m && ny >= 0 && ny < n)
// 조건 2. 방문하지 않았으며 (maps[nx][ny] === 1)
// 조건 3. 이동 가능한 경우 (!visited[nx][ny])
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !visited[nx][ny] && maps[nx][ny] === 1) {
// 방문 처리
visited[nx][ny] = true;
// 이동후에 좌표에 현재까지의 거리 + 1
maps[nx][ny] = maps[x][y] + 1;
// 해당 방문지 큐에 추가 (다음타겟)
queue.push([nx, ny]);
}
}
}
// 도착지에 도달할 수 없으면 -1 반환
if (maps[m - 1][n - 1] === 1) return -1;
// 최종 목적지까지의 거리 반환
return maps[m - 1][n - 1];
}
(Lv.3) 네트워크 (BFS)
코테가 국어문제인 걸 느낀 게.. 이해 하는데 한참 걸리고 로직을 짜도 많이 이해가 안 갔던 문제
하지만 해결 방법은 몇 가지만 따져보면 금방 해결할 수 있었던 것 같다
- 모든 컴퓨터를 어떻게든 다 탐색해야만한다.
- 한 컴퓨터를 탐색할 때 다른 컴퓨터의 연결관계도 확인해야한다
function solution(n, computers) {
let visited = new Array(n).fill(false);
let cnt = 0;
for (let i=0; i<n; i++) {
// 새로운 컴퓨터를 발견시마다 cnt를 증가시켜줌
// (= 아직 i번째 컴퓨터를 탐색하지 않았다면)
if(!visited[i]) {
cnt++;
let queue = []
queue.push(i)
while(queue.length) {
let currentComputer = queue.shift();
// 여기에서 queue에 담긴 값을 true로 바꿔주기 때문에
// 외부 반복문에서 삽입한 i는 후순위로 처리
visited[currentComputer] = true;
for (let j=0; j<n; j++) {
// ★ 첫번째 컴퓨터와 j번쨰 컴퓨터가 연결되어있고 (1로)
// j번째에 해당하는 컴퓨터를 아직 탐색하지 않으면
// ★ 단, 여기에서 if문에 해당하지 않더라도 for문은 마저 수행
// 만약 여러개가 해당시 여러개를 push
if(computers[currentComputer][j] === 1 && !visited[j]) {
queue.push(j)
}
// if문에 모두 해당하지 않아서 queue가 빈 배열로 나가더라도
// while문을 벗어나 외부 for문을 타므로 정상적 수행
}
}
}
}
return cnt
}결론적으로는 위와 같은 코드가 나옴
여기에서 핵심은
- (외부 반복) 탐색을 하지 않은 컴퓨터만 i를 순차적으로 올리며 탐색
- 새로운 컴퓨터를 발견시 cnt값을 늘림 (★네트워크가 될 수 있으므로 -> 네트워크가 맺어져도 괜찮고 안 맺어진다면 어차피 다음에 1개가 더 늘어나니까)
- while문을 통해 탐색하며 방문함을 표시함
- 현재 탐색중인 컴퓨터와 j번째 컴퓨터가 연결 되어 있고 아직 j번쨰 컴퓨터를 탐색하지 않았다면 queue에 j번째 컴퓨터를 넣어줌
- 여기에서 queue에 j번째를 넣고 외부 반복문을 타더라도 j가 선순위가 되고 i가 후순위가 되므로 정상적 실행이 가능
생각보다 어려웠다...
위 코드를 dfs로 푼다면?
function solution(n, computers) {
let visited = new Array(n).fill(false); // 방문 여부를 기록할 배열
let cnt = 0; // 네트워크 개수
// DFS 함수 정의
function dfs(currentComputer) {
visited[currentComputer] = true; // 현재 컴퓨터 방문 처리
// 현재 컴퓨터와 연결된 다른 컴퓨터 탐색
for (let j = 0; j < n; j++) {
if (computers[currentComputer][j] === 1 && !visited[j]) {
dfs(j); // 연결된 컴퓨터로 재귀 호출
}
}
}
// 모든 컴퓨터를 순회하며 DFS 탐색 시작
for (let i = 0; i < n; i++) {
if (!visited[i]) {
cnt++; // 새로운 네트워크 발견 시 증가
dfs(i); // 새로운 네트워크에 대한 DFS 탐색 시작
}
}
return cnt;
}
트리 탐색의 핵심처럼 재귀 같은 반복이 이루어 짐
여기에선 dfs를 통해 j값을 확인 한 후
한 번의 for문을 더 돌며 visited의 모든 요소를 탐색함
다 풀고 나서야 알았지만 이런 문제는 큐 관리의 복잡성을 피하기 위해 보통 dfs를 더 많이 활용한다고 함
게다가 "연결된 모든 노드를 탐색하는 문제"로, DFS의 깊이 우선 탐색이 자연스럽게 잘 맞는다고 함
-> 한 컴퓨터의 모든 연결된 점을 확인하고 연결 되어있으면 dfs를 통해 j번째를 실행하면 되기 떄문
-> 반복이 안 되면 아래의 반복문을 통해 다음 차례의 dfs를 수행하면 됨
(Lv.3) 단어 변환 (BFS)
내가 처음에 짰던 코드
function solution(begin, target, words) {
// 예외처리
// if (words.indexOf(target) === -1) return 0
// indexOf말고 includes 쓰기
if (words.indexOf(target) === -1) return 0
let visited = [];
let queue = [];
queue.push([begin, 0])
for(let i=0; i<words.length; i++) {
// 큐의 길이가 존재하고 visited가 words[i]번쨰가 없을 때
if (queue.length && visited.indexOf(words[i]) === -1) {
// 큐에서 꺼내와서
let [currentWord, cnt] = queue.shift();
console.log('currentWord: ', currentWord,' / cnt: ', cnt)
let diff = 0;
for(let j=0; j<begin.length; j++) {
// diff의 값을 따져본 후에
if (currentWord[j] !== words[i][j]) {
diff++
}
if (diff > 1) {
break
}
if (diff === 1) {
let newWord = words[i]
if (newWord === target) return cnt
cnt++
if (!visited.includes(newWord)) {
queue.push([newWord, cnt]);
visited.push(newWord);
}
}
}
}
console.log('visited', visited)
console.log('queue', queue)
}
// 이 문제는 한 인덱스를 집중적으로 보니까 dfs일 것 같음
// 각 단어의 길이만큼을 각 스펠링으로 나누어 배열에 삽입 (2차원 배열로 변경)
// 각 배열을 순회하며 해당하는 자신과 다른애가 가장 적은애를 찾아
// 앞 인덱스부터 자기와 다른 인덱스를 맞바꾸어줌
// 최소한의 단계를 return 해야함
// 만약 words안에 target단어가 없으면 return 0
}풀이
이 문제는 dfs가 아닌 최단 경로를 구하는 것이기 때문에 bfs로 풀어야함
function solution(begin, target, words) {
// indexOf 쓰지 말고 inlcudes 쓰기
if (!words.includes(target)) return 0;
let visited = [];
let queue = [];
// 초기값 삽입
queue.push([begin, 0]);
// while문 세팅
while (queue.length > 0) {
let [currentWord, cnt] = queue.shift();
// words를 순회하며 변환 가능한 단어 탐색
for (let i = 0; i < words.length; i++) {
// ★ 이미 방문한 단어는 스킵
if (visited.includes(words[i])) continue;
let diff = 0;
for (let j = 0; j < currentWord.length; j++) {
if (currentWord[j] !== words[i][j]) diff++;
// 1이상이라 어차피 변환 불가능하면 for문 break를 통해 반복문 탈출
// *깨알 기초 다지기 : continue는 해당 조건만 스킵, break는 반복문 완전 스킵
if (diff > 1) break;
}
// 1인 애만
if (diff === 1) {
// 그떄의 words[i]를 새로운 단어에 넣어줌
let newWord = words[i];
// 만약 새로운 단어가 target값과 동일하다면 여태에 +1 해주고 바로 return
if (newWord === target) return cnt + 1;
// 아직 일치 하지 않으면, 바뀐 단어와 현재까지의 cnt+1을 통해 dfs재반복
queue.push([newWord, cnt + 1]);
// visited에 기록
visited.push(newWord);
}
}
}
}생각해보면 단순한 문제지만 어렵게 생각해서 너무 어렵게 생각해서 어렵게 접근하게 된 문제인 것 같다.
- includes를 통해 words가 정답을 갖고 있지 않다면 바로 종료
- queue에 초기에 시작값인 begin과 0을 전달
- while을 통하d여 bfs반복
- visited에 방문했던 단어가 있다면 continue를 통해 해당 단어를 스킵하고 diff를 통해 다른 게 2개 이상일 땐 break를 통해 반복문 자체를 종료함
- diff가 1일 때만 그때의 단어를 변수에 지정하여 해당 변수가 목표값과 같다면 함수를 종료하고, 그렇지 않으면 queue와 visited에 삽입해주어서 다시 또 bfs를 수행하면 됨
dfs, bfs에 대한 명확한 구분 후에 어떤식으로 접근할지 설계를 더 하고 다가가면 쉬울 것 같음
(Lv.3) 아이템 줍기
전체 풀이코드, 처음엔 주어진 좌표를 2배할 생각도 없고 이유도 몰랐지만 풀다보면서 헤매다보니 어찌저찌 2배를 해서 푸는 게 더 낫다고 확인이 들었던 문제
function solution(rectangle, characterX, characterY, itemX, itemY) {
// 1. 좌표 확장: 모든 좌표를 2배로 확장하여 정수 좌표만 다룰 수 있게 처리
const expanded = rectangle.map(([x1, y1, x2, y2]) => [x1 * 2, y1 * 2, x2 * 2, y2 * 2]);
const startX = characterX * 2;
const startY = characterY * 2;
const endX = itemX * 2;
const endY = itemY * 2;
// 2. 문제에 주어진 크기의 2배를 하여 0으로 채워진 그리드 생성
const size = 101;
const grid = [];
for (let i=0; i<size; i++) {
grid.push(new Array(size).fill(0))
}
// 3. 사각형 테두리에 포함되는 그리드를 1으로 바꿈
expanded.forEach(([x1, y1, x2, y2]) => {
// 상단, 하단 테두리 설정
// x는 x1 ~ x2까지
for (let x = x1; x <= x2; x++) {
grid[x][y2] = 1; // 상단 테두리
grid[x][y1] = 1; // 하단 테두리
}
// 좌측, 우측 테두리 설정
// y는 y1 ~ y2까지
for (let y = y1; y <= y2; y++) {
grid[x1][y] = 1; // 좌측 테두리
grid[x2][y] = 1; // 우측 테두리
}
});
// 4. 테두리 제외 0으로 변경
expanded.forEach(([x1, y1, x2, y2]) => {
// x는 x1+1부터 x2-1까지
for (let x = x1 + 1; x < x2; x++) {
// y는 y1+1부터 y2-1까지
for (let y = y1 + 1; y < y2; y++) {
grid[x][y] = 0; // 내부 좌표 제거
}
}
});
// 5. 방문 여부를 기록할 배열 생성
let visited = [];
for (let i=0; i<size; i++) {
visited.push(new Array(size).fill(false))
}
visited[startX][startY] = true;
// 7. BFS 탐색을 위한 큐 초기화 및 시작점 방문 처리
const queue = [];
queue.push([startX, startY]);
// 8. 이동 방향 (dx: 열 이동, dy: 행 이동)
const dx = [-1, 0, 1, 0];
const dy = [0, 1, 0, -1];
// 9. BFS 탐색 시작
while (queue.length) {
const [x, y] = queue.shift(); // 현재 좌표를 가져옴
// 4방향 탐색
for (let i = 0; i < 4; i++) {
const nx = x + dx[i]; // 다음 열(가로 좌표)
const ny = y + dy[i]; // 다음 행(세로 좌표)
// 유효 범위 내에 있고, 방문하지 않았으며, 테두리인 경우
// ★ 유의점 : 항상 범위내를 먼저 탐색하고 visited와 grid를 탐색해야함
if (nx >= 0 && nx < size && ny >= 0 && ny < size && !visited[nx][ny] && grid[nx][ny] === 1) {
visited[nx][ny] = true; // 방문 처리
grid[nx][ny] = grid[x][y] + 1; // 이동 거리 기록
queue.push([nx, ny]); // 큐에 추가
}
}
}
// 10. 최종 결과 반환 (확장된 좌표계에서의 거리를 원래 거리로 복원)
const originResult = Math.floor(grid[endX][endY] / 2);
return originResult;
}이번 문제를 풀면서 어느 정도 BFS에 감을 잡은 것 같다.
다시 정리를 해보자면
- 좌표, 출발점, 도착지 2배
- 2배된 사이즈에 해당하는 그리드를 생성 (0)
- 반복문을 돌며 (x1, y1, x2, y2 는 문제에서 주어진 좌표값)에 해당하는 태두리 부분들을 1로 바꾸어줌
- 테두리가 아닌 내부 부분은 expanded 배열의 각 사각형을 돌며 내부를 0으로 바꾸어줌
- 2배된 사이즈에 해당하는 visited 생성
- queue 초기세팅 후 bfs 진행
- 그 후로 늘 하던대로 바깥에 선언한 dx, dy와 i가 4까지의 반복문을 돌며 아직 탐색하지 않았고, visited가 false이며 주어진 그리드 내부에 해당하는 애들을 방문처리하고 이동거리를 기록하며 큐에 추가
- ★ 여기에서, visited와 gird를 처리하기 전에 미리 좌표 내부의 영역에 대한 탐색을 먼저해야 런타임 에러가 발생하지 않음!
그나마 조금 더 bfs에 친해진 문제.. 최단 경로를 탐색할 땐 항상 주의하고 염두하며 풀어야겠다!
(Lv.3) 여행 경로 (DFS)
여행 '경로'이기 때문에 모든 곳을 탐색하는 dfs가 활용될 걸 알았다 다행히 문제에서 출발지점이 ICN인 걸 알려줘서 접근이 쉬웠다
기억해야할 점은
a[1] - b[1]을 쓰지 말고
알파벳순 정렬할 거면 a[1].localeCompare([b1]))을 사용해야한다는것풀이
function solution(tickets) {
// 시작점 지정
const route = ["ICN"];
// 티켓을 도착지 기준으로 알파벳 순 정렬.
tickets.sort((a, b) => a[1].localeCompare(b[1]));
// 각 공항의 방문 여부를 기록하는 배열 초기화.
const visited = new Array(tickets.length).fill(false);
// DFS 함수 정의.
const dfs = (current) => {
// 경로가 완성되었으면 함수 종료
if (route.length === tickets.length + 1) {
return true;
}
// 모든 티켓을 확인.
for (let i = 0; i < tickets.length; i++) {
// 현재 티켓이 사용되지 않았고, 출발지가 현재 위치와 같다면 탐색.
if (!visited[i] && tickets[i][0] === current) {
// 현재 티켓 사용 처리.
visited[i] = true;
// 도착지를 경로에 추가.
route.push(tickets[i][1]);
// 도착지로 한번 더 dfs 탐색 진행
// 만약 한번 더 진행했다가 위에 종결 조건을 만족하면 그대로 종료 후 반환
if (dfs(tickets[i][1])) return true;
// 백트래킹 진행 (진행한 단계 무효화)
// 현재 경로가 유효하지 않거나,
// 모든 티켓을 사용하였지만 경로가 완성되지 않았을 때
visited[i] = false;
route.pop();
}
}
};
dfs("ICN");
return route;
}
- dfs를 호출하면서 for문을 돌며 전체 탐색
- 아직 방문하지 않았고 방문한 곳의 처음이 현재에 current값이라면 그 도착지인 값을 route에 추가해주고 그 값으로 한번 더 dfs를 진행
- ★ 여기에서, 만약 혹시 만약 현재 경로가 유효하지 않거나 경로가 완성되지 않았을 때는 백트래킹을 두어 그때에 단계를 무시하면 된다!! 없으면 안 되는 케이스들이 몇 있었따
- dfs의 초입부에 종결 조건문 (탈출조건)을 추가하여 그 값을 통해 함수를 마무리
내가 생각하는 핵심
- dfs의 초입에 탈출 조건을 제시하고 dfs 반복문 내부에서 dfs를 돌며 탈출하는 것이 나에게는 더 맞는 것 같음
- 문제가 잘 해결되지 않았을 떄나 아니면 TC가 다 맞다해도 혹시 모를 백트래킹을 삽입하는 것은 좋은 것 같음
옛날 나의 코드
function solution(tickets) {
let answer = [];
const result = [];
const visited = [];
tickets.sort();
const len = tickets.length;
const dfs = (str, count) => {
result.push(str);
if(count === len) {
answer = result;
return true;
}
for(let i = 0; i < len; i++) {
if(!visited[i] && tickets[i][0] === str) {
visited[i] = true;
if(dfs(tickets[i][1], count+1)) return true;
visited[i] = false;
}
}
result.pop();
return false;
}
dfs("ICN", 0);
return answer;
}이거 아마 한번에 풀었을텐데 나름 잘했다는 생각이 듦
