바이러스
문제 해결 아이디어
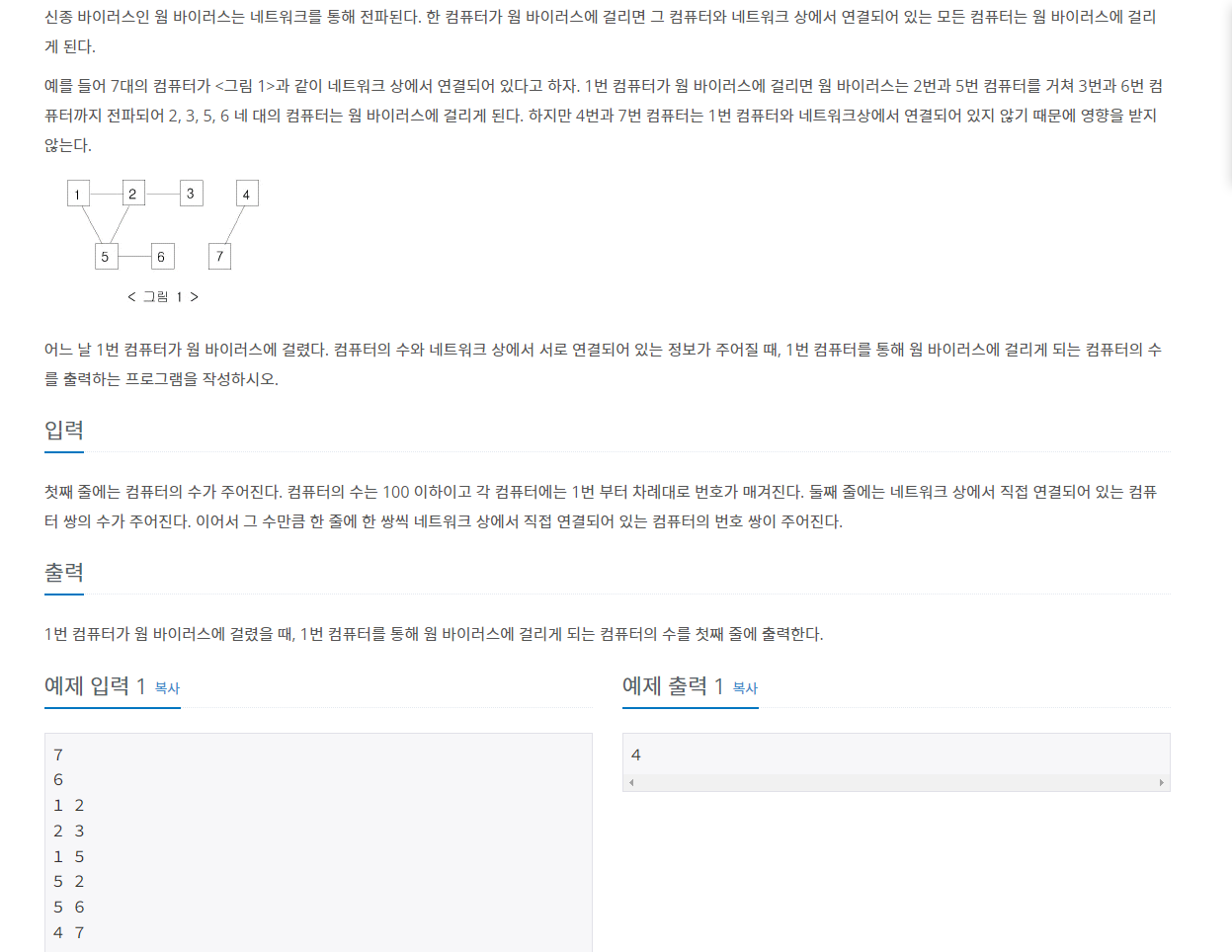
1번 노드에서 도달할 수 있는 다른 노드의 개수를 출력하는 문제
DFS를 이용해 양방향 그래프에 대한 그래프 탐색을 진행인덱스 0을 사용하지 않아서 직관적으로 나타냄
풀이
function solution()
{
let n = 7 // 정점의 갯수
let m = 6 // 간선의 갯수
let graph = [[1, 2], [2, 3], [1, 5], [5, 2], [5, 6], [4, 7]]
// 답 : 4 ----------------------------------------------
let graph2 = [];
for (i=1; i<=n; i++) graph2[i] = [] // 앞에 빈 아이템 1개 + 7개의 빈 배열 생성
for (let i=1; i< graph.length; i++) {
let x = graph[i][0]
let y = graph[i][1]
graph2[x].push(y)
graph2[y].push(x)
}
console.log(graph2)
let cnt = 0;
let visited = new Array(graph.length).fill(false); // 방문을 저장할 배열
function dfs(x) {
visited[x] = true;
cnt++ // 방문 했으면 cnt의 값을 1증가
for (let y of graph2[x]) {
if (!visited[y]) dfs(y)
}
}
dfs(1)
// 1번 노드를 예를 들면, 1번 노드에서 다른 노드로 이동 가능한 노드의 갯수가 정답
console.log(cnt-1)
}설명
DFS의 가장 기본적인 문제
일종의 연결고리들을 확인하는 문제라고 생각하면 됨
유기농 배추
https://www.acmicpc.net/problem/1012
문제해결 아이디어
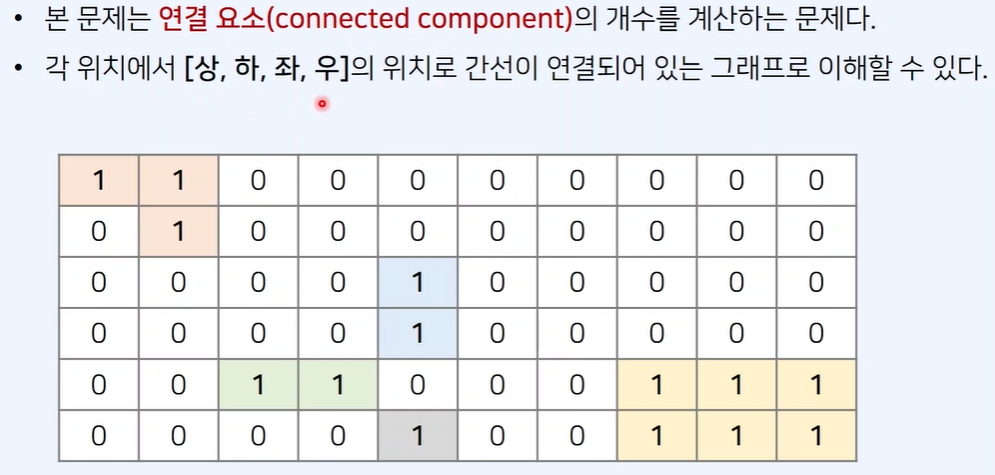
연결 요소는 일종의 [묶음]으로 이해하면 직관적
왼쪽 위부터 오른쪽 아래까지 하나씩 확인하며 처리되지 않은 원소에 대해 DFS를 호출
풀이
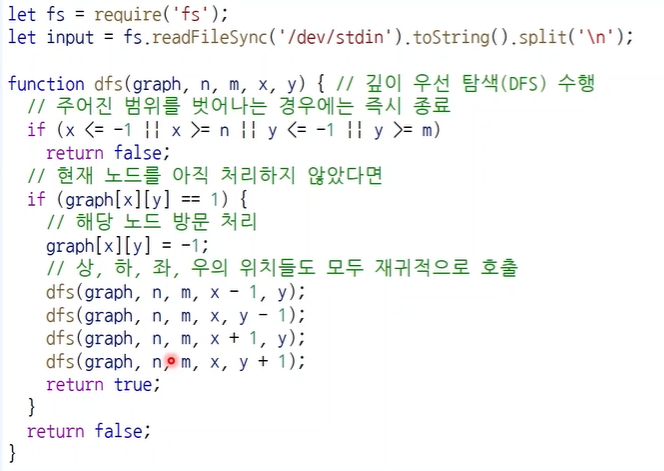

주어진 배열의 길이만큼 0으로된 배열을 만든 후
주어진 좌표의 값에 배추 (1)를 심는다.
그 후 이중 포문을 통해 각 좌표값에 대해 dfs를 실시하면 된다.
dfs에서는 해당하는 값이 1일 경우 방문의 증표로 -1을 실행함 동시에 4개의 dfs (상, 하, 좌, 우)를 실행하여 근처에 이어져 있는 1들도 -1을 계산해준다.
그렇게 한 덩어리씩 없애가면 됨
결론적으로,
사라지지 않은 처음 1을 발견다면 즉, 덩어리가 있을 때마다 answer값을 늘려주면 됨
노드사이의 거리
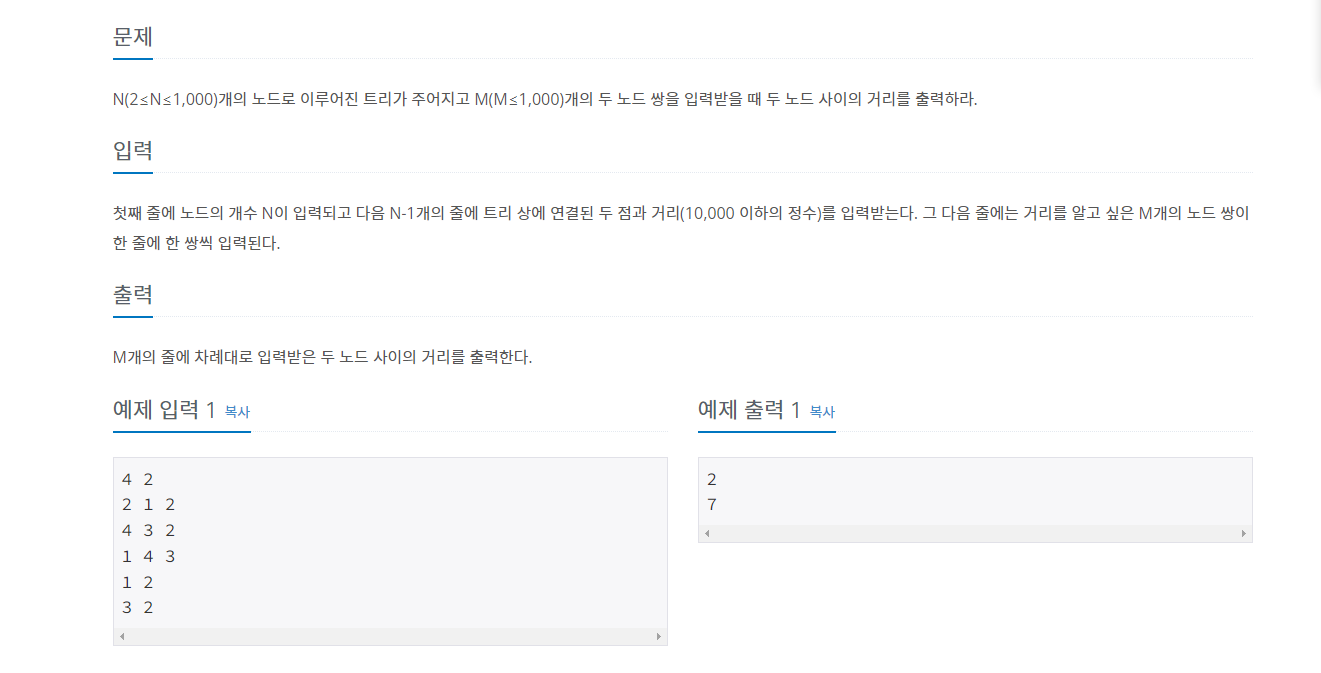
모든 노드에 대해 방문을 하므로 방문(완전탐색) 할 때 연결 간선의 수를 구하거나 거리를 구할 수 있음
문제 해결 아이디어
트리가 양방향 간선으로 구성되어 있다고 가성
노드의 개수 N은 최대 1천
항상 트리형식이므로 간선은 N-1개트리 내에 존재하는 노드 A와 B의 거리를 구하기 위한 시간 복잡도는 O(N)
핵심 아이디어 요약
트리에서는 임의의 두 노드 간의 경로가 오직 1개
트리에선 BFS가 아닌 DFS로도 간단한 최단거리를 계산할 수 있음단순히, 매 쿼리마다 노드 A에서 B까지의 거리를 계산하여 거리표를 만들어줌
풀이
function solution()
{
let n = 4 // 정점의 갯수
let m = 2 // 간선의 갯수
let tree = [[2, 1, 2], [4, 3, 2], [1, 4, 3], [1, 2], [3, 2]]
// 답 : 4 ----------------------------------------------
let graph = [];
for (i=1; i<=n; i++) graph[i] = [] // 앞에 빈 아이템 1개 + 4개의 빈 배열 생성
// "연결작업" (노드의 갯수 -1까지)
for (let i=0; i<n-1; i++) { // 노드의 갯수가 4개이므로 간선의 갯수는 3개 간선 3개를 서로 연결해줌
let x = tree[i][0]
let y = tree[i][1]
let cost = tree[i][2]
graph[x].push([y, cost])
graph[y].push([x, cost])
}
function dfs(x, dist) {
if (visited[x]) return // 이미 방문한 곳이라면 종료
visited[x] = true // 그게 아니라면 선 방문처리 후
distance[x] = dist // 들어온 거리
for (let [y, cost] of graph[x]) { // for문을 통해 자기랑 연결된 애들이 여러 개여도 가능
dfs(y, dist + cost) // 각 좌표에대한 거리를 표시
}
}
for (let i=0; i < m; i++) {
let x = tree[tree.length-2+i][0] // 1
let y = tree[tree.length-2+i][1] // 2
// 매 쿼리 (문제) 마다 visited와 distance를 초기화
visited = new Array(n+1).fill(false)
distance = new Array(n+1).fill(-1) // -1인 이유는 0이면 도달했다는 것이니 -1로
dfs(x, 0) // 노드 x에서 기준, 자기로부터 떨어진 모든 노드의 길이를 구할 수 있음
console.log(distance[y]) // [1, 2]처럼 내가 수행한 곳(1)에서 2까지의 거리
}
}