High-Performance Large-Scale Image Recognition Without Normalization[.,2021]
.png)
Summary
Batch Normalization은 computer vision task에 많이 사용됩니다. 그러나 batch normalization은 batch size에 dependent하다는 단점을 지닌다.
본 연구에서는 좀 더 stable하게 학습하기 위하여 adaptive gradient clipping을 제안하였고, 기존 ResNet structure를 변형한 Normalizer-Free ResNets(NFNets)을 제안한다.

위 그림은 개별적인 model이 Imagenet data에 대한 training latency 및 accuracy를 나타낸다. NFNet-F1 model이 EffNet-B7와 비교하였을때, 높은 accuracy를 가진다는 사실을 도출 할 수 있다. 또한 NFNet-F0, EffNet-B5를 비교하였을때 NFNet-F0의 training latency가 적게 걸린다는 사실을 알 수 있습니다.
Contents
- Batch-norm의 benefit & 한계점 [Introduction]
- Normalization 없는 Resnets. [Related work]
- Adaptive gradient clipping [Related work]
- NFNets [Method]
- Experiments
- Conclusions
Introduction
Batch normalization
BN은 여러 장점을 지닌 방법론으로 설명됩니다.
- BN은 loss landscape를 smoothing시켜준다. → Link
- 학습하는데 있어 좀더 stable하게 학습이 진행된다. 이는 batch size를 키우거나, 를 키워서 학습할 수 있습니다.
- BN은 mean-shift를 줄여주는 효과를 지닌다.
- ReLU같은 비대칭 activation인 경우, mean-shift현상이 일어나게 되는데 BN을 적용하게 되면 각각의 channel에 대하여 batch들의 평균이 0에 근접하게 Normalization됩니다. 이로써 mean-shift를 줄일 수 있습니다.
- BN은 residual branch를 downscale하는 역할을 합니다.
- Resnet의 Basicblock을 보면 BN이 존재하는데, BN은 학습하는데 있어 데이터의 variance를 suppress한다.
그러나 batch normalization은 아래와 같은 단점을 가집니다.
- Computing cost가 많이 듭니다.
- 학습할때, mini batch의 ,를 계산하고 저장한다는 점에서 expensive하다.
- Train/inference할때 다르게 연산됩다.
- inference할때, 학습을 통해 얻은 최종적인 , 를 사용하여 moving average 기법적용
- 학습하는데 있어 batch의 statistics의 variance가 크다면, 성능이 저하됩다.
- 이는 batch size에 dependent하다고 설명 할 수 있으며 (batch size에 sensitivie하다는 판단).
- 만약 batch size가 작다면, 성능이 저하된다.
Related work
pre-activated Resnets
Pre-activated Resnets은 기존 Resnets의 residual block을 변형한 모델입니다.

위의 그림을 보시면 resnet의 residual block과 full pre-activation의 block structure가 다른 것을 확인할 수 있습니다. full pre-activation의 구조는 다음과 같습니다.
pre-activation structure
👉 BN → ReLU → weight → BN → ReLU → weight본 연구에서는 pre-activated Resnets을 기반으로 NFNets을 제안하였습니다.
Normalizer-Free Resnets(NFNets)
위에서 언급하였듯이, BN의 단점을 극복하기 위하여 최근 들어 많은 연구가 진행중에 있습니다.
본 연구에서는 NFNets을 제안하였습니다. (pre-activation ResNets class[2016])
Pre-activation ResNets model에서 BN을 제외하고 residual block을 다음과 같이 변형하였습니다. 이전의 residual block과 차이가 있다면 BN제거 및 , 를 추가 하였습니다.
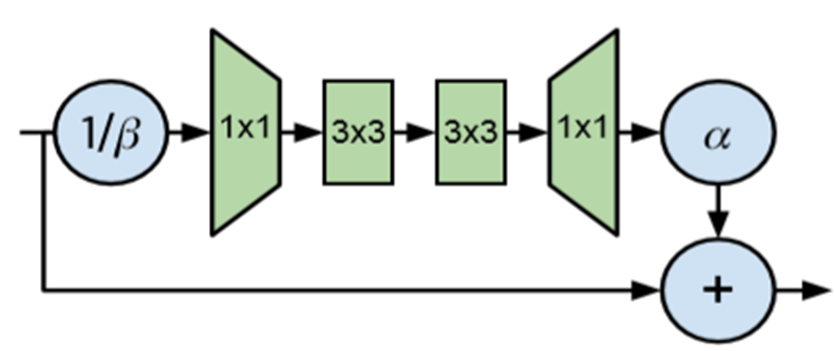
변형된 Residual block
는 residual block의 input을 의미하고, 는 residual branch에서 계산된 값을 의미합니다.
- 는 각각의 residual block 이후 활성화함수의 분산이 증가하는 속도를 의미합니다. ( = 0.2)
- 는 residual block의 input (과 동일)의 std를 의미합니다.
Residual block의 input ()은 downscale됩니다.
Scaled Weight Standardization
다음은 2021년 Brock이 제안한 Scaled Weight Standardization을 적용하여 activation의 mean-shift를 방지하였습니다. Convolution layer인 경우, 아래와 같이 표현할 수 있다.
지난번에 리뷰했던 Layer Normalization을 비롯하여 여러가지 Normalization을 다뤘습니다. weight standardization의 도식화를 보겠습니다.
Layer Normalization
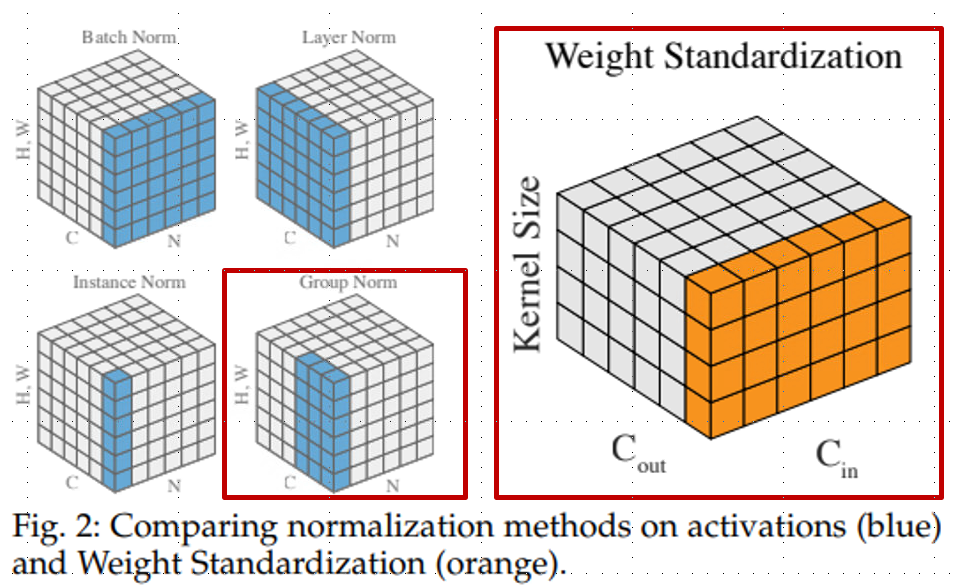
왼쪽에 있는 그림들은 batch 혹은 channel 중점적으로 normalization을 진행하였습니다. 이에 반해 Weight standardization은 convolution filter를 대상으로 normalization을 수행합니다. 이 방법은 loss landscape를 smoothing 하는 효과를 가져옵니다.
본 연구에서는 Scaled Weight Standardization을 제안
- activation function들은 -scaled activation function에 의해 scaling
-scaled activation function
- ReLu →
Regularization method(e.g., dropout) 추가
NFNets의 최종적인 residual block

단점 : Batch size에 sensitive함
Adaptive Gradient Clipping for Efficient Large-Batch Training
NFNets의 단점을 보완하기 위하여 NFNets에 adaptive gradient clipping을 적용하였습니다.
Adaptive gradient clipping을 설명하기 전에 앞서 gradient clipping을 간략하게 설명하도록 하겠습니다. 수식은 아래와 같습니다.
여기서 는 gradient vector, 는 threshold 를 의미합니다.
을 이용하여 의 norm을 억제하는 방법인데, gradient clipping인 경우 threshold에 매우 sensitive하다는 사실을 알 수 있습니다.
이러한 한계를 극복하기 위해 저자는 Adaptive gradient clipping을 제안하였습니다. 수식은 다음과 같습니다. matrix라 가정하겠습니다.
Notation
-
-
: 번째 layer의 weight matrix
-
: 의 gradient
-
: norm
이때, 는 다음과 같은 수식으로 표현 가능합니다.
AGC는 번째 layer의 weight matrix 와 의 ratio 즉, 을 수식을 기반으로 gradient descent step이 해당 layer의 weight matrix를 변화시키는데에 초점을 두었습니다.
그러나 의 경우는 다음과 같은 문제가 있습니다. 만약 의 변화량이 크면 학습하는데 있어 unstable할 수도 있습니다.
본 연구에서는 unit-wise ratios of gradient norms을 적용하였습니다. 수식은 다음과 같습니다.
여기서 는 번째 layer의 weight matrix인 의 gradient를 나타냅니다. 이때 는 row를 의미합니다.
는 위와 동일하나 = 로 정의됩니다.
Experiments
AGC의 성능 확인
모델로는 pre-activation NF-ResNet-50, NF-ResNet-200 / dataset은 ImageNet을 사용하였습니다.
- Optimizer : SGD / 90 Epochs / Batch size : 256 ~ 4096 / = 0.1
- = [0.01, 0.02, 0.04, 0.08, 0.06]
.png)
왼쪽 그림은 ResNet, NF-ResNet에 w/o AGC, AGC에 따른 accuracy를 보여줍니다. NF-ResNet에 AGC를 적용하지 않았을때, batch size를 키우니 Accuracy가 하락하는 양상을 보입니다. 반면 AGC를 적용하면 batch size를 키워도 학습이 stable하고, baseline(BN)보다 성능이 나아짐을 보입니다.
오른쪽 그림은 ResNet50에 batch size, 에 따른 accuracy를 나타낸 그래프입니다. batch size가 커짐에 따라 값을 줄여야 한다는 판단
Training time비교
.png)
위 그래프는 Test GFLOPS에 대한 accuracy를 의미합니다. GFLOPS이 동일할때(같은 속도로 연산을 수행) NFNet-F1, EffNet-B7의 accuracy를 확인하게 되면 NFNet-F1의 acc가 더 높다는 사실을 알 수 있었습니다. 그럼 GFLOPS이 동일할때, 학습 시간은 어느정도 걸릴까요? 이는 다음 표에서 설명하도록 하겠습니다.
Imagenet data에 대하여 NFNets evaluation
.png)
위의 테이블을 보시면 각 Model의 #FLOPs, #Params, Top-1, Top-5, TPUv3 Train/GPU Train time을 볼 수 있다. EffNet-B7, NFNet-F1 을 비교해보면 NFNet-F1의 학습시간이 EffNet-B7보다 적다는 사실을 알 수 있고, Top-1,Top-5는 다소 높다는 사실을 알 수 있습니다.
Model fine-tuning after pre-training
.png)
300M labeled image를 pre-training 한 BN/NF-ResNET 모델을 fine-tuning하여 ImageNet data에 대해 학습을 진행하였다. batch size는 2048, = 0.1을 주었다. 이때 column의 의미하는 바는 input Image의 shape을 의미한다. [224, 320, 384]
결론적으로 BN-ResNet보다 NF-ResNet이 좀더 좋은 성능을 보였음을 알 수 있다.
Conclusion
단순의 batch normalization을 적용하지 않은 model은 large-scale dataset에 대하여 오히려 낮은 성능을 보인다. 이러한 한계를 극복하기 위해 저자는 AGC를 제안한다.
Adaptive Gradient Clipping을 적용함으로써 large-batch를 학습하는데 있어 stable 해졌고, strong augmentation도 잘 optimize하였다.
BN제거 후 residual branch의 변경 및 Scaled weight Standardization을 적용한 Normalizer-Free Nets은 transfer learning에도 좋은 성능을 보였다.
동일한 Flops기준으로 computation을 수행할때, 학습시간 관점에서 baseline에 비해 효율적임을 확인할 수 있었다.
