문제

n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

제한 사항

• 섬의 개수 n은 1 이상 100 이하입니다.
• costs의 길이는 ((n-1) * n) / 2이하입니다.
• 임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
• 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
• 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
• 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예시

costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.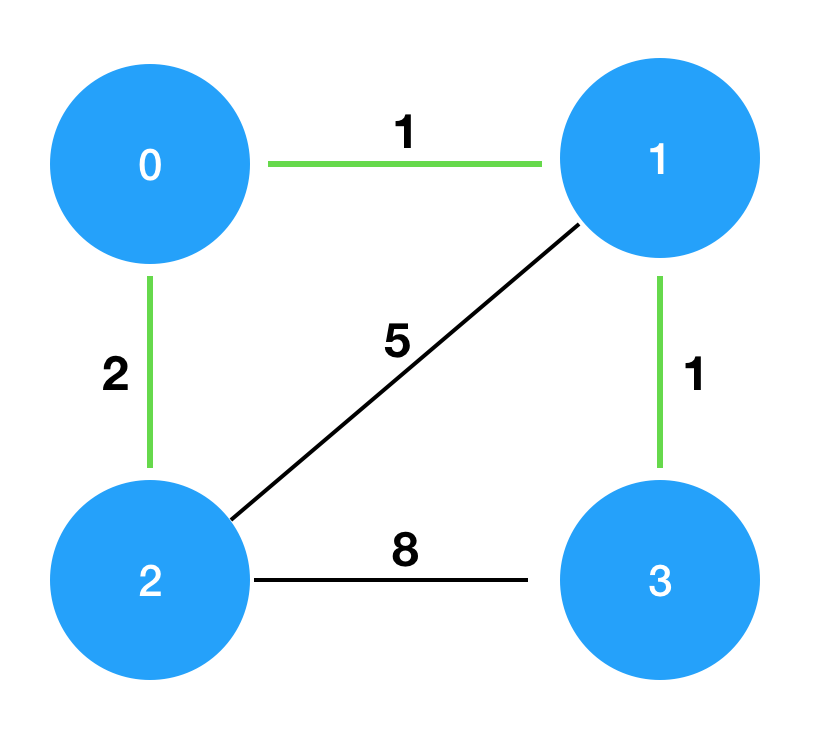

풀이

아이디어

• 이 문제는 '간선에 가중치가 포함되어 있는 그래프에서, 모든 정점을 최소 비용으로 연결'하는 문제입니다.
• 따라서, 크루스칼 알고리즘을 사용할 수 있겠습니다.
• 크루스칼 알고리즘을 활용하려면 Union-Find 알고리즘도 사용해야 합니다.

1. 먼저 가중치를 기준으로 오름차순 정렬을 합니다. (크루스칼 알고리즘의 시작과 동일)
   • 이때 python에서는 sort 함수의 key 파라미터에 원하는 기준원소를 넘겨서 가중치 기준으로 오름차순 정렬이 가능합니다.
2. parent 배열을 초기화합니다.
3. 정렬된 costs 배열을 돌면서 union, find 연산을 실행합니다. 이에 따라서 만약 두 정점의 부모가 모두 같지 않은 경우(사이클이 생기지 않는 경우), MST(최소 스패닝 트리)에 들어가는 것이므로 union 연산을 해주고, answer에 해당 가중치를 더합니다.

코드

def solution(n, costs):
    answer = 0
    #비용을 기준으로 오름차순 정렬
    costs.sort(key = lambda x: x[2])
    #부모 리스트
    parent = [i for i in range(n)]

    #find함수
    def find(x):
        if parent[x] != x:
            parent[x] = find(parent[x])
        return parent[x]
    #union함수
    def union(a, b):
        a, b = find(a), find(b)
        if a < b:
            parent[b] = a
        else:
            parent[a] = b
    
    for src, dest, cost in costs:
        if find(src) != find(dest):
            union(src, dest)
            answer += cost

    
    return answer

C++ 코드

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>

using namespace std;

int find(int x, vector<int> &parent) {
    if(x != parent[x]) {
        parent[x] = find(parent[x], parent);
    }
    return parent[x];
}

void union_f(int a, int b, vector<int> &parent) {
    a = parent[a];
    b = parent[b];
    
    if (a < b) {
        parent[b] = a;
    } else {
        parent[a] = b;
    }
}

int solution(int n, vector<vector<int>> costs) {
    //parent 벡터 초기화
    vector<int> parent(n);
    for(int i=0; i<n; i++) {
        parent[i] = i;
    }
    
    //비용기준으로 오름차순으로 정렬
    sort(costs.begin(), costs.end(), [](const vector<int>& a, const vector<int>& b) {
        return a[2] < b[2];
    });
    
    //정렬된 그래프정보를 순회하면서 정답 업데이트
    int answer = 0;
    for(const auto& edge : costs) {
        int a = edge[0];
        int b = edge[1];
        if(find(a, parent) != find(b, parent)) {
            union_f(a, b, parent);
            answer += edge[2];
        }
    }
    
    return answer;
}