알고리즘

트리는 노드(Node)로 이루어진 자료구조입니다. 트리를 이해하기 위한 좋은 방법 중 하나는 재귀적 설명법을 사용하는 것입니다.트리는 하나의 루트 노드를 갖는다. (그래프 이론에서 꼭 이래야할 필요는 없지만, 보통 일반적인 프로그래밍, 면접의 트리에선 맞는 말이라고 할

사실, 트리(tree)는 그래프(graph)의 한 종류 입니다. 하지만 그렇다고 모든 그래프가 트리는 아닙니다. 트리는 사이클(cycle)이 없는 하나의 연결 그래프 입니다. 그래프는 단순히 노드와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 것과 같습니다.

해시란 임의의 크기를 가진 데이터를 해시함수를 이용하여 고정된 길이의 비트열로 변환하는 것을 말한다.해시를 만들기 위해선 해시 함수가 필요한데 해시 함수는 임의의 길이의 데이터를 고정된 길이의 데이터를 출력하는 함수이다. 말 그대로 해시 함수는 해시를 만드는 함수이다.

동적 계획법의 등장 배경은 피보나치 수열을 통해 알 수 있다. 피보나치 수열은 제2항까지는 1, 제3항부터는 바로 앞의 두 항을 더한 수로 정의된다. 제0항은 생략하기도 한다. 수열은 아래와 같다.프로그래밍에서 피보나치 수열은 보통 재귀를 통해 표현한다.아래는 피보나치

그래프 최단 거리 구하는 알고리즘1. 다익스트라(Dijkstra)2. 벨만-포드(Bellman-Frod)3. 플로이드-와샬(Floyd-Wrasahll)다익스트라(Dijkstra) 알고리즘그래프의 최단 경로 구하는 알고리즘하나의 정점에서 출발하는 최단 거리를 구함(출발지

그래프 최단 경로 구하는 알고리즘하나의 정점에서 출발하는 최단 거리를 구함(출발지만 정함)음수 사이클 없어야 함(음수 가중치 허용)O(nm) 시간 복잡도 가짐동적 계획법 사용, relaxation 기법최단 거리 구하는 알고리즘에서 출발지 하나를 고르는 것은 다익스트라와

그래프 최단 거리 구하는 알고리즘1. 다익스트라(Dijkstra)2. 벨만-포드(Bellman-Frod)3. 플로이드-와샬(Floyd-Wrasahll)플로이드-와샬(Folyd-Warshall) 알고리즘그래프의 최단 경로 구하는 알고리즘 하나모든 정점에서 모든 정점까지

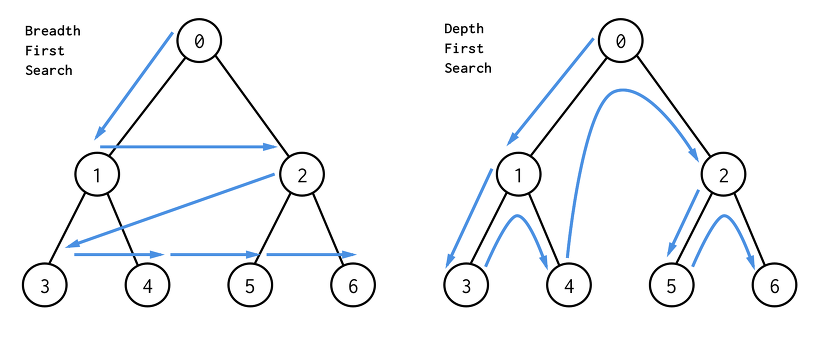
프로그래밍에 자주 사용되는 대표적인 자료구조에는 "그래프"가 있습니다. 그래프는 정점과 간선으로 이루어져 있는데 간선을 통해서 모든 정점을 방문하는 것을 그래프를 탐색한다고 합니다.위에서 언급했듯이 그래프 탐색 알고리즘에는 대표적으로 깊이 우선 탐색(DFS), 너비 우