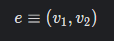그래프

1. 개요

그래프는 정점(Vertex)과 정점들을 연결하는 변(Edge)으로 구성이 된다. 일반적으로 정점은 원으로 표현하고 변은 화살표나 선분으로 표현한다. 변을 화살표로 나타내는 경우에는 해당 방향으로만 이동할 수 있으며, 이러한 그래프를 유향 그래프(Directed graph)라고 말한다. 반대로 선분으로 표현되는 경우에는 양방향 모두 이동이 가능하며, 이러한 그래프를 무향 그래프(Undirected graph)라고 말한다. 그리고 변의 경우에는 특정한 수치를 가질 수 있는데 이를 가중치(Weighted value)라고 말한다.

많은 그래프가 있지만 나는 유향, 무향, 가중을 정리하였다.

2. 그래프

1) 용어와 정의

그래프(graph) $G$는 꼭짓점의 집합 $V$와 변의 집합 $E$의 순서쌍으로 정의된다. 즉,

$G≡(V,E)$

당연하게도 $V$의 원소는 꼭짓점(vertex), $E$의 원소는 변(모서리, edge)라 부른다. 흔히 그림에서 꼭짓점은 점이나 원으로 표현되고, 변은 두 끝점을 잇는 선분으로 표현된다.

변의 집합 $E$는 모든 $e∈E$가 $v_1, v_2 ∈V$에 대해

$e ={ v_1, v_2 }$

가 되도록 정의한다. 이 때 $v_1$, $v_2$를 $e$의 끝점(endpoint)이라 하고, $v_1$과 $v_2$는 서로 인접한다(adjacent) 또는 이웃한다(neighbor)고 한다. '$e$는 $v_1$, $v_2$와 붙어있다(incident)' 또는 '$v_1, v_2$ 를 연결한다(connect)'고 한다. 두 꼭짓점 $v_1, v_2$를 연결하는 변을 간단히 $v_1v_2$와 같이 표기하기도 한다.

2) 유향그래프

그래프의 정의 중 $e \in E$에 대한 정의를 다음과 같이 바꾸어 준 것을 유향그래프(directed graph, digraph)라고 한다.

$e≡(v_1, v_2)$

보다시피, 순서를 나타내기 위해 집합이 아닌 순서쌍을 이용하였다. 여기서 ee는 유향변(방향모서리, directed edge 또는 arc)이라고 한다. 이때, $v_1$은 ee의 시점, $v_2$은 ee의 종점이라 하며, '$e$는 $v_1$에서 시작하여 $v_2$에서 끝난다', 또는 '$v_1$에서 $v_2$ 로 간다'와 같이 표현한다. 흔히 그림에서 유향변은 시점에서 종점으로 향하는 화살표로 표현된다.

한편, 유향그래프가 아닌 그래프를 무향그래프(비방향성 그래프, undirected graph)라 한다.

유향그래프는 무향그래프와 달리 두 정점 사이의 단방향적인 관계를 표현할 수 있다.

3) 가중 그래프

가중 그래프(weighted graph)는 각각의 변에 가중치(weight)라 불리는 값을 대응한 그래프이다. 엄밀하게는 가중치 함수 $W : E \to \mathbb{R}$를 추가한 그래프로 정의할 수 있다.

가중치는 그래프 모델이 쓰이는 상황에 따라 다르게 정의되어 다양하게 활용될 수 있다. 예를 들어 비행기의 항로를 그래프로 모델링한다면, 운항 거리, 시간, 항공비 등을 가중치로 고려할 수 있는데, 최단 경로 문제의 풀이법을 이용하면 '목적지까지 가장 빨리, 비용이 적게 도착할 수 있는 항공편은?' 같은 질문에 답할 수 있게 된다.

출처 : 나무위키 그래프