OBST
보통 OBST(Optimal Binary Search Tree)는 사전에서 단어를 찾을때 많이 사용된다.
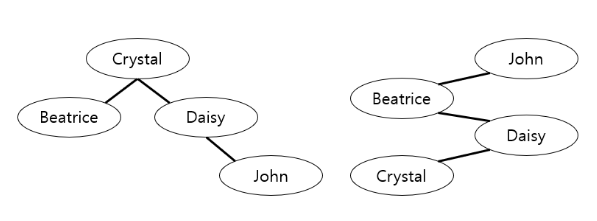
검색을 할때는 루트 노드부터 시작해서 재귀함수를 호출하면서 아래로 내려가기 때문에, 검색할 대상이 아래쪽에 있을수록 함수 호출을 해야 하는 횟수가 늘어난다.
위 그림에서 검색 대상이 Crystal이라고 하자. 왼쪽에서는 바로 결과가 나오지만 오른쪽에서는 3번이나 내려가야 한다. 금방 검색결과를 얻기 위해서는 BST를 최대한 적은 층수로 구성하는게 좋다. 하지만, 현실에서는 단어별로 검색 요청이 들어오는 빈도가 다르다.
따라서 많이 호출되는 것은 더 빨리 찾을 수 있게 배치하는게 좋다.
이렇게 빈도까지 고려해서 배치를 하기 위해서는 '평균 검색 시간'이 필요한데,
평균검색 시간 = 검색빈도*필요 탐색횟수를 모두 더한 것이다.
예를들어, Crystal = 0.1 / Daisy = 0.2 / Beatrice = 0.3 / John = 0.4 이라고 하면
이러한 결과가 나온다. 오른쪽이 더 효율 결과가 좋다고 할 수 있다.
이렇게 검색을 했을때, 평균 검색시간이 가장 낮은 효율적인 트리를 찾는게 OBST 이다.
어떻게 하면 최적의 BST를 찾아 낼 수 있을지 찾아보기 위해서 모양을 전부다 만들어 볼 수는 없다. 예를 들어 n개의 노드의 모양을 찾아보려면 서브노드로 왼쪽 오른쪽 2가지 경우가 있기 때문에 루트를 제외한 가지의 경우의 수가 존재한다.
따라서 최적의 BST를 찾기 위해서 Dynamic programming을 사용한다.
subproblem인 서브트리들이 각각 OBST여야 부모트리도 최적트리이다.
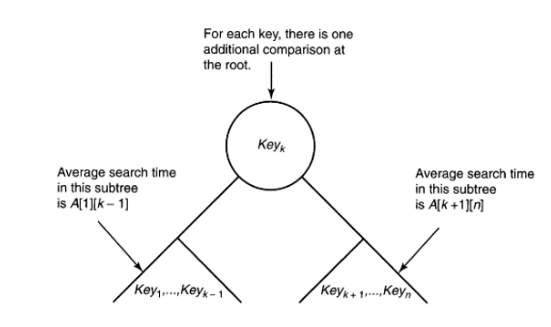
왼쪽과 오른쪽이 각각 OBST라면
평균 검색 시간 = 서브트리에서 찾는 시간 + 루트노드를 탐색하는 시간이다.
이걸 식으로 만들어보면,
i번째 key부터 j번째 key까지 OBST를 만들었다고 하자.
이때 평균 검색 시간(최적값)을 A[i][j]라고 하자.
루트노드가 k번째 key일때
왼쪽 서브트리의 평균 검색 시간 = A[i][k-1]
오른쪽 서브트리의 평균 검색 시간 = A[k+1][j]
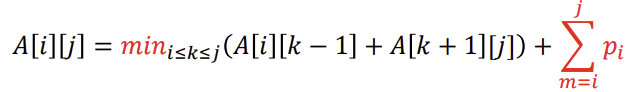
: 루트가 뭐가 될지 결정되지 못한채로 노드가 일자로 있다고 생각하고 (깊이가 모두 1이다.) 모든 노드의 frequency를 더해준다.
노드 1에서 n까지의 확률을 모두 한번씩 더해주고, k가 루트이기 때문에 1~(k-1)까지의 최적 평균검색시간과 (k+1)~n까지의 최적 평균 검색시간을 더해주면 A[1][n]의 최적 평균검색시간을 구할 수 있다.

A[i][j] : i->j 까지 노드를 생성했을때 평균 검색시간
R[i][j] : i->j 까지 노드를 생성했을때 평균 검색시간이 가장 짧았던 경우의 수 중 root였던 key의 index
왜 저런 표가 나왔는지 구해보자.
A[1][1] ~ A[4][4] : 모두 자기 자신 하나밖에 없으므로 자신의 빈도 값을 써준다.
A[1][2] : 1,2 노드 생성
1과 2의 확률을 더해준다.
이제 둘중 뭐가 root일때 더 작은지 구한다. 여기서는 둘다 같으므로, 1을 선택해준다. R[1][2] = 1을 넣어준다.
A[2][3] : 2,3 노드 생성
위와 마찬가지로 2와 3의 확률을 더해준다.
2가 루트인 경우: 3이 한 레벨 밑으로 내려가므로 3의 확률을 더해준다. 을 더해주고
3이 루트인 경우는 2가 한 레벨 밑으로 내려가므로 2의 확률을 더해준다. 확률을 확인해보면 둘중 2가 루트인 경우가 더 평균 검색시간이 작다.
따라서 을 해준다.
A[1][3] 같은 경우는 어떻게 해야할까??
일단 노드 1 2 3 을 생성한다. 1과 2와 3의 확률을 모두 더해준다.
이제 1 or 2 or 3이 root일때 평균검색시간을 확인해본다.
root -> 1 : 2와3이 child node이다. 2->3 은 아까 구해놨다. 이다.
root -> 2: 2를 중심으로 1과 3이 child이다. 1과 3이 한레벨씩 밑으로 내려갔으므로, 확률을 하나씩 더해준다.
root -> 3: 3이 root이므로 1->2인 이다
이중 가장 작은것은 루트가 2일때 이다.
모두 더하면 이다.
그리고 R[1][3]=2를 해준다.
참고로 평균 검색시간이 가장 적을 루트 노드의 경우의 수를 구할때, 값이 같다면 레벨이 낮은 것을 고른다.
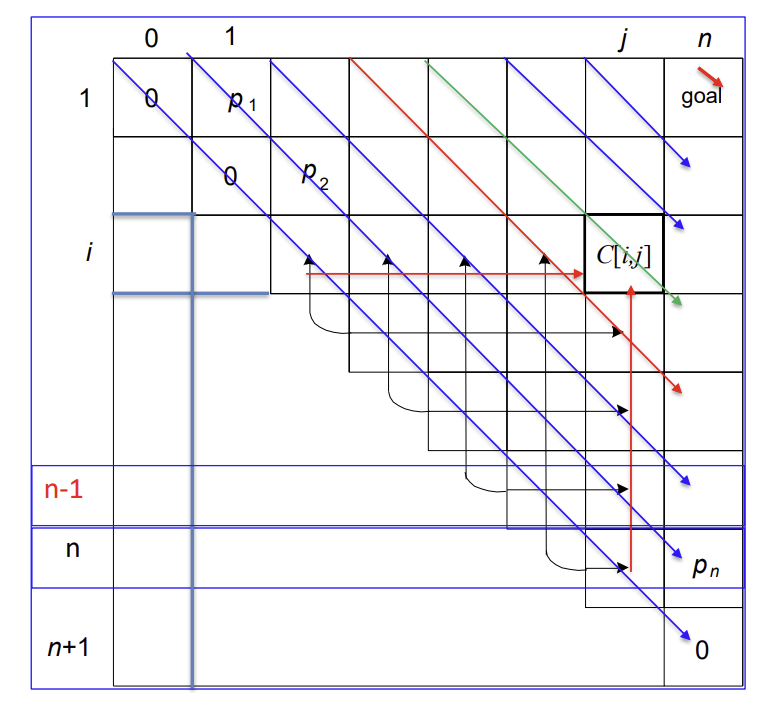
구현을 할때는 위 그림의 순서로 평균 탐색 시간을 구해야 한다.
한줄을 모두 구하고 다음줄로 넘어가는 식으로 작성하는 코드를 예를 들어보자.
A[0][3]을 구하려고 할때 root가 0이라면 A[1][3]을 더해줘야 한다.
하지만 이때 A[1][3]이 아직 구해지지 않아 값을 넣을 수 없다.
따라서 위와 같이 대각선으로 구해야 한다.
time complexity
구현
import java.util.Arrays;
class OptimalBST{
public static void main(String args[]){
//freq는 0~3 인덱스를 갖는다.
float[] freq = {0.1F,0.2F,0.3F,0.4F};
Obst o = new Obst();
o.findOptimal(freq);
System.out.println("A[][]");
for(int i = 0; i<freq.length; i++)
System.out.println(Arrays.toString(o.A[i]));
System.out.println();
System.out.println("R[][]");
for(int i = 0; i<freq.length; i++)
System.out.println(Arrays.toString(o.R[i]));
}
}
class Obst {
float A[][] = new float[4][4]; //비용 저장할 배열
int R[][] = new int[4][4]; //최적 비용일때 root 값 저장할 배열
float min;// 최적 비용 구할때 사용.
float total_cost; // 전체 비용 저장
float root_cost = 0F; // 루트 비용 저장한값
public void findOptimal(float[] freq) {
//노드가 하나일때 자신의 값을 비용으로 한다.
for (int i = 0; i < freq.length; i++) {
A[i][i] = freq[i];
R[i][i] = i;
}
//이차원 배열을 대각선 순으로 구할 수 있도록 한다.
// 예를들어 [0][1] -> [1][2] -> [2][3] -> [0][2] -> [1][3] -> [2][4]...
for (int l = 1; l < freq.length; l++) {
for (int i = 0; i < freq.length - 1; i++) {
for (int j = i + l; j == i+l && j < freq.length; j++) {
if(i >= j) break; // root 순서는 무조건 i->j 방향
total_cost = 0;
min = 1000;
root_cost = 0;
//평균탐색 시간을 구한다.
for(int idx = i; idx <= j; idx++ ){ // 노드의 frequency를 모두 더한다.
root_cost += A[idx][idx];
}
for(int k = i; k <= j; k++){ //root가 k일때
if(k == 0) total_cost = root_cost + A[k+1][j];
else if(k == j) total_cost = root_cost + A[i][k-1];
else total_cost = root_cost + A[i][k-1] + A[k+1][j];
if(min > total_cost){
min = total_cost;
R[i][j] = k;
}
}
A[i][j] = total_cost;
}
}
}
}
}
결과:
A[][]
[0.1, 0.4, 1.0, 2.0]
[0.0, 0.2, 0.7, 1.5999999]
[0.0, 0.0, 0.3, 1.0]
[0.0, 0.0, 0.0, 0.4]
R[][]
[0, 1, 1, 2]
[0, 1, 2, 2]
[0, 0, 2, 3]
[0, 0, 0, 3]
