아래는 Introduction to Algorithms의 챕터 3장을 요약한 내용입니다. 각 문제는 점근 표기법(Asymptotic Notation)과 알고리즘 분석의 핵심 개념을 다루고 있습니다.
3.1: 성장 함수 (Growth of Functions)
- 3.1-1: 삽입 정렬(Insertion Sort)의 하한을 ( n )이 3의 배수가 아니어도 ( \Omega(n^2) )로 수정. ( \lfloor n/3 \rfloor )로 조정해 증명.
- 3.1-2: 선택 정렬(Selection Sort)의 실행 시간은 비교 횟수 기준 ( \Theta(n^2) ), 입력에 무관.
- 3.1-3: 삽입 정렬 하한을 ( \alpha n )개의 큰 값이 앞에 있을 때 일반화. ( \alpha \leq 1/2 ) 제한, ( \alpha = 1/4 )에서 최대 ( (1/8)n^2 ) 이동.
3.2: 점근 표기법의 표준 표기와 속성 (Standard Notations and Common Properties)
- 3.2-1: ( \max{f(n), g(n)} = \Theta(f(n) + g(n)) ), 상한 ( c_2 = 1 ), 하한 ( c_1 = 1/2 ).
- 3.2-2: "최소 ( O(n^2) )"는 상한을 하한처럼 오해해 의미 없음.
- 3.2-3: ( 2^{n+1} = O(2^n) ) (참), ( 2^{2n} \neq O(2^n) ) (거짓).
- 3.2-4: ( \Theta = O \cap \Omega ) 증명.
- 3.2-5: ( T(n) = \Theta(g(n)) )는 최악 ( O(g(n)) )와 최선 ( \Omega(g(n)) )의 결합.
- 3.2-6: ( o(g(n)) \cap \omega(g(n)) = \emptyset ), 극한 모순.
- 3.2-7: ( O(g(n,m)) ), ( \Omega(g(n,m)) ), ( \Theta(g(n,m)) )를 두 변수로 정의.
3.3: 점근 표기법의 추가 속성 (Additional Properties)
- 3.3-1: 단조 증가 함수 ( f, g )에 대해 ( f + g ), ( f(g) ), ( f \cdot g ) (비음수 시)도 단조 증가.
- 3.3-2: ( \lfloor \alpha n \rfloor + \lceil (1 - \alpha) n \rceil = n ) (0 ≤ ( \alpha ) ≤ 1).
- 3.3-3: ( (n + o(n))^k = \Theta(n^k) ), ( \lceil n \rceil^k, \lfloor n \rfloor^k )도 동일.
- 3.3-4: ( \lg(n!) = \Theta(n \lg n) ), 지수 속성, ( \lg(\Theta(n)) = \Theta(\lg n) ).
- 3.3-5: ( \lceil \lg n \rceil! )는 다항 한정 아님, ( \lceil \lg \lg n \rceil! )는 다항 한정.
- 3.3-6: ( \lg^(\lg n) > \lg(\lg^ n) ) (점근적 크기).
- 3.3-7: 황금비 ( \phi )와 공액 ( \hat{\phi} )가 ( x^2 = x + 1 ) 만족.
- 3.3-8: 피보나치 수 ( F_i = \frac{\phi^i - \hat{\phi}^i}{\sqrt{5}} ) (귀납법).
- 3.3-9: ( k \lg k = \Theta(n) )면 ( k = \Theta(n / \lg n) ).
3-1: 다항식의 점근 행동
- 문제: ( p(n) ) (차수 ( d ))와 상수 ( k )에 대해:
- ( k \geq d ): ( O(n^k) ).
- ( k \leq d ): ( \Omega(n^k) ).
- ( k = d ): ( \Theta(n^k) ).
- ( k > d ): ( o(n^k) ).
- ( k < d ): ( \omega(n^k) ).
- 요약: ( p(n) )의 차수와 ( k ) 비교로 점근 관계 결정.
3-2: 상대적 점근 성장
- 문제: 쌍(A, B)에 대해 ( O, o, \Omega, \omega, \Theta ) 여부 판단.
- 요약: 예: ( n^k = o(n^{k+\epsilon}) ), ( c^n = \omega(n^k) ), 로그 vs. 다항 비교.
3-3: 점근 성장률 순서
- a: 30개 함수를 느린 순으로 정렬, ( \Theta ) 클래스 분할 (예: ( 1, n^2, n!, 2^n )).
- b: ( f(n) = n ) (짝수), ( 2^n ) (홀수)로 어느 ( g_i(n) )와도 ( O )나 ( \Omega ) 아님.
- 요약: 함수 성장 속도 순위화 및 특이 함수 정의.
3-4: 점근 표기 속성
- 문제: 참/거짓 판별.
- a. ( O(g) \not\Rightarrow O(f) ) (거짓).
- b. ( f + g \neq \Theta(\min) ) (거짓).
- c. ( O(g) \Rightarrow \lg = O(\lg g) ) (참).
- d. ( 2^{f(n)} = O(2^{g(n)}) ) (참).
- e. ( O(f^2) ) (거짓).
- f. ( O(g) \Rightarrow \Omega(f) ) (참).
- g. ( \Theta(f(n/2)) ) (거짓).
- h. ( f + o(f) = \Theta(f) ) (참).
- 요약: 점근 속성의 참/거짓 검증.
3-5: 점근 표기 조작
- 문제: 등식 증명.
- a. ( \Theta(\Theta(f)) = \Theta(f) ).
- b. ( \Theta(f) + O(f) = \Theta(f) ).
- c. ( \Theta(f) + \Theta(g) = \Theta(f + g) ).
- d. ( \Theta(f) \cdot \Theta(g) = \Theta(f \cdot g) ).
- e-g. 일부 누락, 합/곱 관련 추정.
- 요약: ( \Theta )의 합/곱 성질 확인.
3-6: ( O )와 ( \Omega ) 변형
- 문제:
- a. ( f = O(g) ) 또는 ( \Omega_\infty(g) ) (참).
- b. 둘 다 아닌 경우 존재 (예: 진동 함수).
- c. ( \Omega_\infty ) 장단점: 무한 성장 포착 vs. 덜 엄격.
- d. ( O' )로 Theorem 3.1 수정.
- e. Soft-oh (( \tilde{O}, \tilde{\Omega}, \tilde{\Theta} )) 정의 및 증명.
- 요약: 변형된 점근 표기의 특성 분석.
3-7: 반복 함수
- 문제: ( f^*(n) )의 반복 횟수 계산.
- a. ( n-1, c=0 ): ( n ).
- b. ( \lg n, c=1 ): ( \lg^* n ).
- c. ( n/2, c=1 ): ( \lg n ).
- d. ( n/2, c=2 ): ( \lg n ).
- f. ( n^{1/3}, c=1 ): ( \log_{3/2} n ).
- g. ( n^{1/3}, c=2 ): ( \log_{3/2} (n/2) ).
- 요약: 각 ( f(n) )에 대한 반복 횟수.
전체 요약
Ch 3은 점근 표기법의 정의, 속성, 함수 성장 비교, 그리고 알고리즘 분석의 기초를 다룹니다. 삽입/선택 정렬의 하한부터 다항식, 로그, 지수 함수의 점근 행동, 황금비와 피보나치 수, 반복 함수까지 이론적 기반을 제공하며, 실무적 적용(예: EHR 시스템 효율성)을 이해하는 데도 도움을 줍니다.
3장 연습문제
Let’s tackle these three problems from a theoretical computer science perspective, focusing on sorting algorithms and their lower bounds. I’ll provide detailed explanations and derivations for each, assuming familiarity with insertion sort and selection sort but breaking everything down clearly. These problems seem inspired by Cormen et al.'s Introduction to Algorithms (Chapter 3), so I’ll align with that style.
3.1-1: Modify the Lower-Bound Argument for Insertion Sort
Problem: The standard lower-bound argument for insertion sort often assumes the input size ( n ) is divisible by 3 (e.g., splitting into thirds for inversions). Modify it to handle any ( n ), not necessarily a multiple of 3.
Standard Lower-Bound Argument (for ( n ) divisible by 3)
- Insertion sort’s worst-case runtime is ( \Theta(n^2) ), driven by the number of inversions—pairs ((i, j)) where ( i < j ) but ( A[i] > A[j] ).
- A common argument: Split an array of size ( n ) into three equal parts (each ( n/3 )), with the largest ( n/3 ) values in the first third, middle ( n/3 ) in the last third, and smallest ( n/3 ) in the middle. The largest values must move right, passing through the middle third, yielding many inversions.
- Inversions: Each of the ( n/3 ) largest values moves from the first ( n/3 ) positions to the last ( n/3 ), passing through ( n/3 ) middle positions, giving ( (n/3) \cdot (n/3) = n^2/9 ) inversions, so runtime is ( \Omega(n^2) ).
Issue with Arbitrary ( n )
- If ( n ) isn’t a multiple of 3, ( n/3 ) isn’t an integer (e.g., ( n = 10 ), ( n/3 \approx 3.33 )). We need integer partitions.
Modified Argument
-
Define three regions with sizes as close to ( n/3 ) as possible:
- First region: ( \lfloor n/3 \rfloor ) positions (largest values start here).
- Middle region: ( \lfloor n/3 \rfloor ) or ( \lfloor n/3 \rfloor + 1 ) positions (smallest values start here).
- Last region: Remaining positions (middle values start here).
-
Total size: ( n = \lfloor n/3 \rfloor + m + (n - \lfloor n/3 \rfloor - m) ), where ( m ) (middle size) is ( \lfloor n/3 \rfloor ) or ( \lfloor n/3 \rfloor + 1 ), adjusted to sum to ( n ).
-
Example: ( n = 10 ):
- First: ( \lfloor 10/3 \rfloor = 3 ) (largest: 8, 9, 10).
- Middle: ( \lfloor 10/3 \rfloor = 3 ) (smallest: 1, 2, 3).
- Last: ( 10 - 3 - 3 = 4 ) (middle: 4, 5, 6, 7).
- Initial array: [8, 9, 10, 1, 2, 3, 4, 5, 6, 7].
-
Inversions: The ( \lfloor n/3 \rfloor ) largest values must pass through the middle ( m ) positions to reach the last region.
- Number of inversions ≈ ( \lfloor n/3 \rfloor \cdot m ).
- For ( n = 10 ): ( 3 \cdot 3 = 9 ) inversions from the largest values alone (e.g., (8,1), (8,2), (8,3), etc.).
-
General Lower Bound:
- ( m \approx n/3 ) (either ( \lfloor n/3 \rfloor ) or ( \lfloor n/3 \rfloor + 1 )).
- Inversions ≈ ( \lfloor n/3 \rfloor \cdot \lfloor n/3 \rfloor \geq (n/3 - 1)^2 ).
- As ( n ) grows, this is ( \Omega(n^2) ) (e.g., ( (n/3)^2 = n^2/9 )).
Result
The modified argument uses ( \lfloor n/3 \rfloor ) and adjusts the middle and last regions to fit ( n ), preserving the ( \Omega(n^2) ) lower bound for any ( n ).
3.1-2: Analyze Selection Sort Runtime
Problem: Using reasoning similar to insertion sort’s lower-bound argument, analyze the running time of selection sort (from Exercise 2.2-2).
Selection Sort Algorithm
- For an array of size ( n ):
- Find the minimum element in ( A[0..n-1] ), swap it with ( A[0] ).
- Find the minimum in ( A[1..n-1] ), swap with ( A[1] ), etc.
- Repeat until the array is sorted.
Pseudocode
def selection_sort(A):
for i in range(len(A)):
min_idx = i
for j in range(i + 1, len(A)):
if A[j] < A[min_idx]:
min_idx = j
A[i], A[min_idx] = A[min_idx], A[i]Runtime Analysis (Similar to Insertion Sort)
-
Comparisons:
- Iteration ( i = 0 ): ( n-1 ) comparisons.
- Iteration ( i = 1 ): ( n-2 ) comparisons.
- ...
- Iteration ( i = n-2 ): 1 comparison.
- Total: ( (n-1) + (n-2) + \cdots + 1 = n(n-1)/2 ).
-
Swaps: Exactly 1 swap per iteration, total ( n-1 ) (or ( n ) if we count trivial swaps when ( min_idx = i )).
-
Worst-Case Input: Unlike insertion sort, selection sort’s runtime doesn’t depend on inversions—it always scans the entire unsorted portion.
- Example: Reverse-sorted array [5, 4, 3, 2, 1].
- Same comparisons regardless of order: ( 4 + 3 + 2 + 1 = 10 ) for ( n = 5 ).
-
Lower-Bound Reasoning:
- Consider a reverse-sorted array split into three parts (like insertion sort’s argument).
- For ( n = 9 ): [7, 8, 9, 4, 5, 6, 1, 2, 3].
- Selection sort still performs ( 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 ) comparisons, unaffected by initial placement.
- The algorithm must compare each element in the unsorted portion, yielding ( \Omega(n^2) ) comparisons.
Result
- Time Complexity: ( \Theta(n^2) ) for comparisons in all cases (best, average, worst).
- Swaps: ( \Theta(n) ), but comparisons dominate.
3.1-3: Generalize Insertion Sort Lower Bound with ( \alpha )
Problem: Generalize the insertion sort lower-bound argument where the ( \alpha n ) largest values start in the first ( \alpha n ) positions (( 0 < \alpha < 1 )). What restriction on ( \alpha ) is needed? What ( \alpha ) maximizes the number of times the ( \alpha n ) largest values pass through the middle ( (1 - 2\alpha)n ) positions?
Generalized Argument
-
Setup:
- Array size ( n ), ( \alpha n ) is the number of largest values (assume integer for simplicity, or use ( \lfloor \alpha n \rfloor )).
- First ( \alpha n ) positions: ( \alpha n ) largest values.
- Next ( (1 - 2\alpha)n ) positions: Smallest values (middle region).
- Last ( \alpha n ) positions: Middle values.
-
Constraint: ( 0 < \alpha < 1 ), and the middle region must be non-negative: ( 1 - 2\alpha \geq 0 ), so ( \alpha \leq 1/2 ).
-
Example: ( n = 9 ), ( \alpha = 1/3 ):
- First ( \alpha n = 3 ): [7, 8, 9].
- Middle ( (1 - 2\alpha)n = (1 - 2/3) \cdot 9 = 3 ): [1, 2, 3].
- Last ( \alpha n = 3 ): [4, 5, 6].
- Initial: [7, 8, 9, 1, 2, 3, 4, 5, 6].
-
Inversions:
- Each of the ( \alpha n ) largest values must move from the first ( \alpha n ) to the last ( \alpha n ), passing through ( (1 - 2\alpha)n ) middle positions.
- Comparisons per value ≈ ( (1 - 2\alpha)n ).
- Total inversions ≈ ( (\alpha n) \cdot (1 - 2\alpha)n = \alpha (1 - 2\alpha) n^2 ).
Restriction on ( \alpha )
- ( \alpha \leq 1/2 ): Ensures the middle region ( (1 - 2\alpha)n \geq 0 ).
- If ( \alpha > 1/2 ), ( 1 - 2\alpha < 0 ), making the middle size negative (invalid).
- Example: ( \alpha = 2/3 ), ( 1 - 2 \cdot 2/3 = -1/3 ), which doesn’t work.
Maximizing Middle Pass-Throughs
- Quantity to Maximize: Number of times the ( \alpha n ) largest values pass through the middle ( (1 - 2\alpha)n ) positions = ( \alpha (1 - 2\alpha) n^2 ).
- Function: ( f(\alpha) = \alpha (1 - 2\alpha) ), domain ( 0 < \alpha \leq 1/2 ).
- Derivative:
- ( f(\alpha) = \alpha - 2\alpha^2 ).
- ( f'(\alpha) = 1 - 4\alpha ).
- Set ( f'(\alpha) = 0 ): ( 1 - 4\alpha = 0 ), ( \alpha = 1/4 ).
- Check Endpoints:
- ( \alpha = 1/4 ): ( f(1/4) = (1/4) \cdot (1 - 2 \cdot 1/4) = 1/4 \cdot 1/2 = 1/8 ).
- ( \alpha = 1/2 ): ( f(1/2) = (1/2) \cdot (1 - 2 \cdot 1/2) = 1/2 \cdot 0 = 0 ).
- ( \alpha \to 0^+ ): ( f(\alpha) \to 0 ).
- Maximum: ( \alpha = 1/4 ) gives ( f(\alpha) = 1/8 ), so inversions = ( (1/8) n^2 ).
Result
- Restriction: ( \alpha \leq 1/2 ).
- Max ( \alpha ): ( \alpha = 1/4 ) maximizes the middle pass-throughs, yielding ( \Omega(n^2) ) inversions.
Summary
- 3.1-1: Adjusted insertion sort lower bound to ( \Omega(n^2) ) for any ( n ) using ( \lfloor n/3 \rfloor ).
- 3.1-2: Selection sort runtime is ( \Theta(n^2) ) due to fixed comparisons, not inversions.
- 3.1-3: Generalized insertion sort bound with ( \alpha \leq 1/2 ), maximized at ( \alpha = 1/4 ).
Let me know if you need further clarification or examples!
Let’s tackle these seven problems from Chapter 3.2, which focus on asymptotic notation and algorithm analysis (likely from Introduction to Algorithms by Cormen et al.). I’ll provide rigorous proofs and explanations for each, keeping them concise yet complete, with examples where helpful. These assume familiarity with ( O ), ( \Omega ), and ( \Theta ) notations, but I’ll define terms as needed.
3.2-1: Prove ( \max{f(n), g(n)} = \Theta(f(n) + g(n)) )
Problem: For asymptotically nonnegative functions ( f(n) ) and ( g(n) ) (i.e., ( f(n) \geq 0 ), ( g(n) \geq 0 ) for large ( n )), prove that ( \max{f(n), g(n)} = \Theta(f(n) + g(n)) ) using the definition of ( \Theta )-notation.
( \Theta )-Notation Definition
( h(n) = \Theta(k(n)) ) means there exist positive constants ( c_1 ), ( c_2 ), and ( n_0 ) such that for all ( n \geq n_0 ):
[ 0 \leq c_1 k(n) \leq h(n) \leq c_2 k(n) ]
Proof
We need to show ( \max{f(n), g(n)} = \Theta(f(n) + g(n)) ), i.e., find ( c_1 ), ( c_2 ), and ( n_0 ) such that:
[ c_1 (f(n) + g(n)) \leq \max{f(n), g(n)} \leq c_2 (f(n) + g(n)) ]
-
Upper Bound (( \max{f(n), g(n)} \leq c_2 (f(n) + g(n)) )):
- By definition, ( \max{f(n), g(n)} = f(n) ) if ( f(n) \geq g(n) ), or ( g(n) ) otherwise.
- Since ( f(n) \leq f(n) + g(n) ) and ( g(n) \leq f(n) + g(n) ) (both ( f ) and ( g ) are nonnegative), we have:
[ \max{f(n), g(n)} \leq f(n) + g(n) ] - Choose ( c_2 = 1 ): ( \max{f(n), g(n)} \leq 1 \cdot (f(n) + g(n)) ).
-
Lower Bound (( c_1 (f(n) + g(n)) \leq \max{f(n), g(n)} )):
- Since ( f(n) \geq 0 ) and ( g(n) \geq 0 ), ( f(n) + g(n) \geq f(n) ) and ( f(n) + g(n) \geq g(n) ).
- Thus, ( f(n) + g(n) \geq \max{f(n), g(n)} ).
- But we need the reverse inequality. Consider:
- If ( f(n) \geq g(n) ), then ( \max{f(n), g(n)} = f(n) ), and ( f(n) \leq f(n) + g(n) ).
- At worst, ( f(n) ) could be much larger than ( g(n) ), but ( \max{f(n), g(n)} ) is still at least half of ( f(n) + g(n) ) in balanced cases.
- Key insight: ( \max{f(n), g(n)} \geq \frac{1}{2} (f(n) + g(n)) ), because ( f(n) + g(n) \leq 2 \max{f(n), g(n)} ) (if one is small, the max dominates).
- Choose ( c_1 = 1/2 ): ( (1/2) (f(n) + g(n)) \leq \max{f(n), g(n)} ).
-
( n_0 ): Since ( f ) and ( g ) are asymptotically nonnegative, choose ( n_0 ) where both are ( \geq 0 ).
Result
[ 0 \leq \frac{1}{2} (f(n) + g(n)) \leq \max{f(n), g(n)} \leq 1 \cdot (f(n) + g(n)) ]
Thus, ( \max{f(n), g(n)} = \Theta(f(n) + g(n)) ).
3.2-2: Why “The running time of algorithm A is at least ( O(n^2) )” is Meaningless
Problem: Explain why this statement doesn’t make sense.
Understanding ( O )-Notation
- ( O(n^2) ) is an upper bound: It denotes a set of functions ( f(n) ) such that ( f(n) \leq c n^2 ) for some constant ( c ) and large ( n ).
- Saying “at least ( O(n^2) )” suggests a lower bound, but ( O )-notation doesn’t imply a minimum.
Why It’s Meaningless
- Interpretation: “At least ( O(n^2) )” might mean the runtime is ( \geq k n^2 ) for some ( k ), but ( O(n^2) ) includes functions like ( n ), ( \log n ), or even constants (since ( n = O(n^2) )).
- Example: If algorithm A runs in ( O(n) ), it’s also in ( O(n^2) ) (since ( n \leq n^2 )). Saying “at least ( O(n^2) )” could imply ( O(n) ) satisfies it, which contradicts the intent of a lower bound.
- Correct Notation: For a lower bound, use ( \Omega(n^2) ) (e.g., “runtime is at least ( \Omega(n^2) )” means ( \geq c n^2 )).
Result
The statement misuses ( O )-notation, conflating upper and lower bounds, rendering it ambiguous and meaningless.
3.2-3: Is ( 2^{n+1} = O(2^n) )? Is ( 2^{2n} = O(2^n) )?
Problem: Check these using the definition of ( O )-notation.
( O )-Notation Definition
( f(n) = O(g(n)) ) if there exist constants ( c > 0 ) and ( n_0 ) such that ( f(n) \leq c g(n) ) for all ( n \geq n_0 ).
-
( 2^{n+1} = O(2^n) ):
- Rewrite: ( 2^{n+1} = 2^n \cdot 2 = 2 \cdot 2^n ).
- Test: ( 2^{n+1} \leq c \cdot 2^n ).
- ( 2 \cdot 2^n \leq c \cdot 2^n ) implies ( c \geq 2 ).
- Choose ( c = 2 ), ( n_0 = 1 ): ( 2 \cdot 2^n \leq 2 \cdot 2^n ) holds.
- Yes, ( 2^{n+1} = O(2^n) ).
-
( 2^{2n} = O(2^n) ):
- Rewrite: ( 2^{2n} = (2^2)^n = 4^n ).
- Test: ( 2^{2n} \leq c \cdot 2^n ).
- ( 4^n \leq c \cdot 2^n ) implies ( (4/2)^n = 2^n \leq c ).
- As ( n \to \infty ), ( 2^n ) grows exponentially, and no constant ( c ) can bound it.
- Check: ( n = 10 ), ( 2^{20} / 2^{10} = 2^{10} = 1024 ); ( n = 20 ), ( 2^{40} / 2^{20} = 2^{20} \approx 1M ). No fixed ( c ) works.
- No, ( 2^{2n} \neq O(2^n) ).
Result
- ( 2^{n+1} = O(2^n) ): Yes.
- ( 2^{2n} = O(2^n) ): No.
3.2-4: Prove Theorem 3.1
Problem: Prove: For any two functions ( f(n) ) and ( g(n) ), ( f(n) = \Theta(g(n)) ) if and only if ( f(n) = O(g(n)) ) and ( f(n) = \Omega(g(n)) ).
Theorem 3.1
( f(n) = \Theta(g(n)) \iff f(n) = O(g(n)) \text{ and } f(n) = \Omega(g(n)) ).
Proof
-
Forward (( \Theta \Rightarrow O \text{ and } \Omega )):
- ( f(n) = \Theta(g(n)) ): ( 0 \leq c_1 g(n) \leq f(n) \leq c_2 g(n) ) for ( c_1, c_2 > 0 ), ( n \geq n_0 ).
- ( f(n) \leq c_2 g(n) ): ( f(n) = O(g(n)) ).
- ( c_1 g(n) \leq f(n) ): ( f(n) = \Omega(g(n)) ).
-
Reverse (( O \text{ and } \Omega \Rightarrow \Theta )):
- ( f(n) = O(g(n)) ): ( f(n) \leq c_2 g(n) ) for ( c_2 > 0 ), ( n \geq n_1 ).
- ( f(n) = \Omega(g(n)) ): ( f(n) \geq c_1 g(n) ) for ( c_1 > 0 ), ( n \geq n_2 ).
- Combine: ( c_1 g(n) \leq f(n) \leq c_2 g(n) ) for ( n \geq \max{n_1, n_2} ), assuming ( g(n) > 0 ) (common in asymptotic analysis).
- Thus, ( f(n) = \Theta(g(n)) ).
Result
Theorem 3.1 holds: ( \Theta ) is the intersection of ( O ) and ( \Omega ).
3.2-5: Prove ( T(n) = \Theta(g(n)) \iff ) Worst-Case ( O(g(n)) ) and Best-Case ( \Omega(g(n)) )
Problem: Show an algorithm’s runtime ( T(n) = \Theta(g(n)) ) if and only if its worst-case time is ( O(g(n)) ) and best-case time is ( \Omega(g(n)) ).
Proof
-
Forward (( T(n) = \Theta(g(n)) \Rightarrow ) Worst ( O ), Best ( \Omega )):
- ( T(n) = \Theta(g(n)) ): ( c_1 g(n) \leq T(n) \leq c_2 g(n) ).
- Worst-case ( T_w(n) \geq T(n) ), so ( T_w(n) \leq c_2 g(n) ) (since ( T(n) \leq c_2 g(n) )), thus ( T_w(n) = O(g(n)) ).
- Best-case ( T_b(n) \leq T(n) ), so ( T_b(n) \geq c_1 g(n) ) (since ( T(n) \geq c_1 g(n) )), thus ( T_b(n) = \Omega(g(n)) ).
-
Reverse (Worst ( O ), Best ( \Omega \Rightarrow T(n) = \Theta(g(n)) ))):
- Worst-case ( T_w(n) = O(g(n)) ): ( T_w(n) \leq c_2 g(n) ).
- Best-case ( T_b(n) = \Omega(g(n)) ): ( T_b(n) \geq c_1 g(n) ).
- For any input, ( T_b(n) \leq T(n) \leq T_w(n) ), so:
[ c_1 g(n) \leq T_b(n) \leq T(n) \leq T_w(n) \leq c_2 g(n) ] - Thus, ( c_1 g(n) \leq T(n) \leq c_2 g(n) ), so ( T(n) = \Theta(g(n)) ).
Result
( T(n) = \Theta(g(n)) ) exactly when worst-case is ( O(g(n)) ) and best-case is ( \Omega(g(n)) ).
3.2-6: Prove ( o(g(n)) \cap \omega(g(n)) = \emptyset )
Problem: Show the intersection of little-o and little-omega sets is empty.
Definitions
- ( f(n) = o(g(n)) ): ( \lim_{n \to \infty} \frac{f(n)}{g(n)} = 0 ) (grows slower than ( g(n) )).
- ( f(n) = \omega(g(n)) ): ( \lim_{n \to \infty} \frac{f(n)}{g(n)} = \infty ) (grows faster than ( g(n) )).
Proof by Contradiction
- Assume ( f(n) \in o(g(n)) \cap \omega(g(n)) ).
- Then:
- ( f(n) = o(g(n)) ): For any ( c > 0 ), ( f(n) < c g(n) ) for large ( n ), and ( \lim f(n)/g(n) = 0 ).
- ( f(n) = \omega(g(n)) ): For any ( c > 0 ), ( f(n) > c g(n) ) for large ( n ), and ( \lim f(n)/g(n) = \infty ).
- Contradiction: The limit ( f(n)/g(n) ) cannot be both 0 and ( \infty ).
- Thus, no such ( f(n) ) exists.
Result
( o(g(n)) \cap \omega(g(n)) = \emptyset ).
3.2-7: Define ( \Omega(g(n, m)) ) and ( \Theta(g(n, m)) ) for Two Parameters
Problem: Given ( O(g(n, m)) = { f(n, m) : \exists c, n_0, m_0 \text{ s.t. } 0 \leq f(n, m) \leq c g(n, m) \text{ for all } n \geq n_0 \text{ or } m \geq m_0 } ), define ( \Omega ) and ( \Theta ).
Definitions
-
( \Omega(g(n, m)) ):
[ \Omega(g(n, m)) = { f(n, m) : \exists c > 0, n_0, m_0 \text{ s.t. } 0 \leq c g(n, m) \leq f(n, m) \text{ for all } n \geq n_0 \text{ or } m \geq m_0 } ]- Lower bound: ( f(n, m) ) grows at least as fast as ( g(n, m) ) when either ( n ) or ( m ) is large.
-
( \Theta(g(n, m)) ):
[ \Theta(g(n, m)) = { f(n, m) : \exists c_1, c_2 > 0, n_0, m_0 \text{ s.t. } 0 \leq c_1 g(n, m) \leq f(n, m) \leq c_2 g(n, m) \text{ for all } n \geq n_0 \text{ or } m \geq m_0 } ]- Tight bound: Combines ( O ) and ( \Omega ) for two-parameter growth.
Explanation
- “( n \geq n_0 ) or ( m \geq m_0 )” means the bound holds when either parameter exceeds its threshold, accommodating independent growth rates.
Example
- ( g(n, m) = n m ):
- ( f(n, m) = 2nm \in \Theta(nm) ) (tight).
- ( f(n, m) = n \in \Omega(nm) ) (lower bound fails unless ( m ) is bounded).
Summary
- 3.2-1: ( \max{f, g} = \Theta(f + g) ) with ( c_1 = 1/2 ), ( c_2 = 1 ).
- 3.2-2: “At least ( O(n^2) )” misuses upper-bound notation.
- 3.2-3: ( 2^{n+1} = O(2^n) ), ( 2^{2n} \neq O(2^n) ).
- 3.2-4: ( \Theta = O \cap \Omega ).
- 3.2-5: ( \Theta ) ties worst-case ( O ) and best-case ( \Omega ).
- 3.2-6: ( o \cap \omega = \emptyset ) due to limit contradiction.
- 3.2-7: Defined ( \Omega ) and ( \Theta ) for two parameters.
Let me know if you want deeper elaboration on any proof!
Let’s tackle these problems from Chapter 3.3, which focus on properties of functions, asymptotic notation, and mathematical relationships (likely from Introduction to Algorithms by Cormen et al.). I’ll provide detailed proofs and explanations, keeping them rigorous yet accessible. Some problems (marked ★) are starred, suggesting extra challenge, so I’ll pay special attention there.
3.3-1: Monotonically Increasing Functions
Problem: Show that if ( f(n) ) and ( g(n) ) are monotonically increasing, then so are ( f(n) + g(n) ) and ( f(g(n)) ). If both are also nonnegative, show ( f(n) \cdot g(n) ) is monotonically increasing.
Definition
A function ( h(n) ) is monotonically increasing if for all ( n < m ), ( h(n) \leq h(m) ) (non-decreasing).
-
( f(n) + g(n) ):
- Given ( n < m ):
- ( f(n) \leq f(m) ) (since ( f ) is monotonically increasing).
- ( g(n) \leq g(m) ) (since ( g ) is monotonically increasing).
- Add: ( f(n) + g(n) \leq f(m) + g(m) ).
- Thus, ( f(n) + g(n) ) is monotonically increasing.
- Given ( n < m ):
-
( f(g(n)) ):
- Since ( g ) is monotonically increasing, ( n < m ) implies ( g(n) \leq g(m) ).
- Since ( f ) is monotonically increasing, ( g(n) \leq g(m) ) implies ( f(g(n)) \leq f(g(m)) ).
- Thus, ( f(g(n)) ) is monotonically increasing.
-
( f(n) \cdot g(n) ) (nonnegative case):
- Given ( f(n) \geq 0 ), ( g(n) \geq 0 ), and ( n < m ):
- ( f(n) \leq f(m) ), ( g(n) \leq g(m) ).
- Since ( f(n) \geq 0 ), ( g(n) \geq 0 ), multiply: ( f(n) g(n) \leq f(m) g(n) ) (because ( g(n) \geq 0 )).
- Then, ( f(m) g(n) \leq f(m) g(m) ) (because ( f(m) \geq 0 ), ( g(n) \leq g(m) )).
- Combine: ( f(n) g(n) \leq f(m) g(m) ).
- Thus, ( f(n) \cdot g(n) ) is monotonically increasing.
- Given ( f(n) \geq 0 ), ( g(n) \geq 0 ), and ( n < m ):
Result
All three functions are monotonically increasing under the given conditions.
3.3-2: Prove ( \lfloor \alpha n \rfloor + \lceil (1 - \alpha) n \rceil = n )
Problem: For integer ( n ) and real ( 0 \leq \alpha \leq 1 ), prove the equation holds.
Proof
-
Let ( k = \lfloor \alpha n \rfloor ), so ( k \leq \alpha n < k + 1 ), where ( k ) is an integer.
-
Then ( \alpha n = k + f ) where ( 0 \leq f < 1 ) (fractional part).
-
Compute ( (1 - \alpha) n ):
- ( (1 - \alpha) n = n - \alpha n = n - (k + f) = (n - k) - f ).
- Since ( 0 \leq f < 1 ), ( n - k - 1 < (n - k) - f \leq n - k ).
- ( \lceil (1 - \alpha) n \rceil = \lceil (n - k) - f \rceil ).
- If ( f = 0 ), ( (n - k) - f = n - k ) (integer), so ( \lceil n - k \rceil = n - k ).
- If ( 0 < f < 1 ), ( n - k - 1 < (n - k) - f < n - k ), so ( \lceil (n - k) - f \rceil = n - k ).
-
Total: ( \lfloor \alpha n \rfloor + \lceil (1 - \alpha) n \rceil = k + (n - k) = n ).
Result
The equation holds for all ( n ) and ( 0 \leq \alpha \leq 1 ).
3.3-3: Show ( (n + o(n))^k = \Theta(n^k) )
Problem: Use equation (3.14) or other means to prove this, then conclude for ( \lceil n \rceil^k ) and ( \lfloor n \rfloor^k ).
Equation (3.14)
[ 1 + o(1) = \Theta(1) ]
- ( h(n) = o(1) ) means ( \lim_{n \to \infty} h(n) = 0 ).
Proof
-
Let ( f(n) = n + o(n) ), so ( f(n) = n (1 + h(n)) ) where ( h(n) = o(1) ), i.e., ( h(n) \to 0 ).
-
Then ( f(n)^k = [n (1 + h(n))]^k = n^k (1 + h(n))^k ).
-
Since ( h(n) \to 0 ), for large ( n ), ( h(n) ) is small, and ( (1 + h(n))^k \to 1^k = 1 ).
-
( (1 + h(n))^k = \Theta(1) ) (since it’s bounded between constants, e.g., ( 1/2 < 1 + h(n) < 2 ) for small ( h(n) ), adjusted by ( k )).
-
Thus, ( n^k (1 + h(n))^k = \Theta(n^k) \cdot \Theta(1) = \Theta(n^k) ).
-
( \lceil n \rceil^k ):
- ( n \leq \lceil n \rceil < n + 1 ), so ( \lceil n \rceil = n + h(n) ) where ( 0 \leq h(n) < 1 ).
- ( h(n)/n < 1/n = o(1) ), so ( \lceil n \rceil = n + o(n) ).
- By above, ( \lceil n \rceil^k = \Theta(n^k) ).
-
( \lfloor n \rfloor^k ):
- ( n - 1 < \lfloor n \rfloor \leq n ), so ( \lfloor n \rfloor = n - h(n) ) where ( 0 < h(n) \leq 1 ).
- ( h(n)/n \leq 1/n = o(1) ), so ( \lfloor n \rfloor = n - o(n) = n (1 - o(1)) ).
- ( \lfloor n \rfloor^k = n^k (1 - o(1))^k = \Theta(n^k) ).
Result
( (n + o(n))^k = \Theta(n^k) ), ( \lceil n \rceil^k = \Theta(n^k) ), ( \lfloor n \rfloor^k = \Theta(n^k) ).
3.3-4: Prove Equations
Problem: Prove:
a. Equation (3.21): ( \lg (n!) = \Theta(n \lg n) ).
b. Equations (3.26)–(3.28): Properties of exponentials.
c. ( \lg(\Theta(n)) = \Theta(\lg n) ).
a. ( \lg (n!) = \Theta(n \lg n) ) (Stirling’s Approximation)
- ( n! = 1 \cdot 2 \cdots n ).
- Stirling’s: ( n! \approx \sqrt{2\pi n} (n/e)^n ).
- ( \lg (n!) \approx \lg (\sqrt{2\pi n}) + n \lg (n/e) = \frac{1}{2} \lg (2\pi n) + n \lg n - n \lg e ).
- Dominant term: ( n \lg n ).
- Bounds:
- Upper: ( n! \leq n^n ), so ( \lg (n!) \leq n \lg n ).
- Lower: ( n! \geq (n/2)^{n/2} ) (middle half), ( \lg (n!) \geq (n/2) \lg (n/2) = \Theta(n \lg n) ).
- Thus, ( \lg (n!) = \Theta(n \lg n) ).
b. Equations (3.26)–(3.28)
- (3.26): ( a^{m+n} = a^m \cdot a^n ):
- ( a^{m+n} = a^{m+n} ), and ( a^m \cdot a^n = a^{m+n} ) (exponent rule).
- (3.27): ( (a^m)^n = a^{mn} ):
- ( (a^m)^n = a^m \cdot a^m \cdots (n \text{ times}) = a^{m \cdot n} ).
- (3.28): ( (ab)^n = a^n b^n ):
- ( (ab)^n = (ab) \cdot (ab) \cdots = (a \cdot a \cdots) \cdot (b \cdot b \cdots) = a^n b^n ).
c. ( \lg(\Theta(n)) = \Theta(\lg n) )
- If ( h(n) = \Theta(n) ), then ( c_1 n \leq h(n) \leq c_2 n ).
- ( \lg h(n) \geq \lg (c_1 n) = \lg c_1 + \lg n ), ( \lg h(n) \leq \lg (c_2 n) = \lg c_2 + \lg n ).
- ( \lg n + \lg c_1 \leq \lg h(n) \leq \lg n + \lg c_2 ), and constants don’t affect ( \Theta ), so ( \lg h(n) = \Theta(\lg n) ).
Result
All proved.
3.3-5: Polynomially Bounded Functions (★)
Problem: Is ( \lceil \lg n \rceil ! ) polynomially bounded? Is ( \lceil \lg \lg n \rceil ! ) polynomially bounded?
Definition
A function ( f(n) ) is polynomially bounded if ( f(n) = O(n^k) ) for some constant ( k ).
-
( \lceil \lg n \rceil ! ):
- Let ( k = \lceil \lg n \rceil \approx \lg n ).
- ( k! \approx \sqrt{2\pi k} (k/e)^k ).
- ( \lg (k!) \approx k \lg k = \lg n \cdot \lg \lg n ).
- Compare to ( n^k ): ( \lg (n^k) = k \lg n ).
- ( k! ) grows faster than any ( n^k ) (exponential in ( k ), while ( n^k ) is polynomial).
- Not polynomially bounded.
-
( \lceil \lg \lg n \rceil ! ):
- Let ( m = \lceil \lg \lg n \rceil \approx \lg \lg n ).
- ( m! \leq (m+1)^m ) (crude upper bound).
- ( m \leq \lg \lg n + 1 ), so ( m! \leq (\lg \lg n + 1)^{\lg \lg n} ).
- ( \lg (m!) \leq \lg \lg n \cdot \lg (\lg \lg n + 1) = o(\lg n) ).
- Compare to ( n^k ): ( \lg (n^k) = k \lg n ), and ( m! ) is sub-polynomial.
- ( m! = O(n^{0.1}) ) (e.g.), so polynomially bounded.
Result
- ( \lceil \lg n \rceil ! ): No.
- ( \lceil \lg \lg n \rceil ! ): Yes.
3.3-6: Compare ( \lg(\lg^ n) ) vs. ( \lg^(\lg n) ) (★)
Problem: Which is asymptotically larger?
Definitions
-
( \lg^* n ): Number of times you apply ( \lg ) to ( n ) until ( \leq 1 ).
- ( \lg^ 2 = 1 ), ( \lg^ 4 = 2 ), ( \lg^* 65536 = 5 ).
-
( \lg(\lg^* n) ):
- ( \lg^ n ) grows very slowly (e.g., ( \lg^ 10^{100} \approx 5 )).
- ( \lg(\lg^* n) \approx \lg 5 ) (constant-like).
-
( \lg^*(\lg n) ):
- ( \lg n ) is large for large ( n ) (e.g., ( \lg 10^{100} = 100 \ln 10 / \ln 2 \approx 332 )).
- ( \lg^(\lg n) = \lg^ 332 \approx 3 ) or 4, still small but grows with ( n ).
-
Comparison: ( \lg^(\lg n) ) increases (slowly) as ( n ) grows, while ( \lg(\lg^ n) ) stabilizes (e.g., ( \lg 5 \approx 2.32 )).
Result
( \lg^*(\lg n) ) is asymptotically larger.
3.3-7: Golden Ratio and Conjugate
Problem: Show ( \phi = \frac{1 + \sqrt{5}}{2} ) and ( \hat{\phi} = \frac{1 - \sqrt{5}}{2} ) satisfy ( x^2 = x + 1 ).
Proof
-
( \phi = \frac{1 + \sqrt{5}}{2} ):
- ( \phi^2 = \left(\frac{1 + \sqrt{5}}{2}\right)^2 = \frac{1 + 2\sqrt{5} + 5}{4} = \frac{6 + 2\sqrt{5}}{4} = \frac{3 + \sqrt{5}}{2} ).
- ( \phi + 1 = \frac{1 + \sqrt{5}}{2} + 1 = \frac{1 + \sqrt{5} + 2}{2} = \frac{3 + \sqrt{5}}{2} ).
- ( \phi^2 = \phi + 1 ).
-
( \hat{\phi} = \frac{1 - \sqrt{5}}{2} ):
- ( \hat{\phi}^2 = \left(\frac{1 - \sqrt{5}}{2}\right)^2 = \frac{1 - 2\sqrt{5} + 5}{4} = \frac{6 - 2\sqrt{5}}{4} = \frac{3 - \sqrt{5}}{2} ).
- ( \hat{\phi} + 1 = \frac{1 - \sqrt{5}}{2} + 1 = \frac{1 - \sqrt{5} + 2}{2} = \frac{3 - \sqrt{5}}{2} ).
- ( \hat{\phi}^2 = \hat{\phi} + 1 ).
Result
Both satisfy the equation.
3.3-8: Fibonacci Number Formula (Missing Equation)
Problem: Prove by induction that the ( i )-th Fibonacci number ( F_i ) satisfies ( F_i = \frac{\phi^i - \hat{\phi}^i}{\sqrt{5}} ).
Proof by Induction
-
Base Cases:
- ( F_0 = 0 ): ( \frac{\phi^0 - \hat{\phi}^0}{\sqrt{5}} = \frac{1 - 1}{\sqrt{5}} = 0 ).
- ( F_1 = 1 ): ( \frac{\phi^1 - \hat{\phi}^1}{\sqrt{5}} = \frac{\frac{1 + \sqrt{5}}{2} - \frac{1 - \sqrt{5}}{2}}{\sqrt{5}} = \frac{\sqrt{5}}{\sqrt{5}} = 1 ).
-
Inductive Step: Assume true for ( i = k-1 ) and ( i = k-2 ):
- ( F{k-1} = \frac{\phi^{k-1} - \hat{\phi}^{k-1}}{\sqrt{5}} ), ( F{k-2} = \frac{\phi^{k-2} - \hat{\phi}^{k-2}}{\sqrt{5}} ).
- ( Fk = F{k-1} + F_{k-2} = \frac{\phi^{k-1} - \hat{\phi}^{k-1}}{\sqrt{5}} + \frac{\phi^{k-2} - \hat{\phi}^{k-2}}{\sqrt{5}} ).
- ( = \frac{\phi^{k-1} + \phi^{k-2} - (\hat{\phi}^{k-1} + \hat{\phi}^{k-2})}{\sqrt{5}} ).
- Factor: ( \phi^{k-1} + \phi^{k-2} = \phi^{k-2} (\phi + 1) = \phi^{k-2} \cdot \phi^2 = \phi^k ) (since ( \phi^2 = \phi + 1 )).
- Similarly, ( \hat{\phi}^{k-1} + \hat{\phi}^{k-2} = \hat{\phi}^k ).
- Thus, ( F_k = \frac{\phi^k - \hat{\phi}^k}{\sqrt{5}} ).
Result
Holds for all ( i ).
3.3-9: ( k \lg k = \Theta(n) ) Implies ( k = \Theta(n / \lg n) )
Problem: Prove this implication.
Proof
- ( k \lg k = \Theta(n) ): ( c_1 n \leq k \lg k \leq c_2 n ).
- Solve ( k \lg k \approx n ):
- Let ( k = \frac{n}{\lg n} v(n) ), where ( v(n) ) is a correction factor.
- Substitute: ( k \lg k = \frac{n}{\lg n} v(n) \lg \left( \frac{n}{\lg n} v(n) \right) = \frac{n}{\lg n} v(n) (\lg n - \lg \lg n + \lg v(n)) ).
- Approximate: ( \frac{n}{\lg n} v(n) \lg n = n v(n) (1 - \frac{\lg \lg n}{\lg n} + \frac{\lg v(n)}{\lg n}) ).
- As ( n \to \infty ), if ( v(n) = \Theta(1) ), then ( k \lg k = \Theta(n) ).
- Check bounds: ( k = c \frac{n}{\lg n} ), then ( k \lg k = c \frac{n}{\lg n} \lg (c \frac{n}{\lg n}) = \Theta(n) ).
- Thus, ( k = \Theta(n / \lg n) ).
Result
Implication holds.
Let me know if you need further clarification!
Let’s solve these problems from Chapter 3 of Introduction to Algorithms by Cormen et al., focusing on asymptotic notation, function growth, and related properties. I’ll provide detailed, rigorous solutions for each, keeping them concise yet complete, with examples where helpful. Some problems have missing subparts (e.g., 3-5e, 3-5f, 3-5g equations), so I’ll address what’s provided and note omissions.
3-1: Asymptotic Behavior of Polynomials
Problem: For a degree-( d ) polynomial ( p(n) = ad n^d + a{d-1} n^{d-1} + \cdots + a_0 ) where ( a_d > 0 ), prove:
a. If ( k \geq d ), then ( p(n) = O(n^k) ).
b. If ( k \leq d ), then ( p(n) = \Omega(n^k) ).
c. If ( k = d ), then ( p(n) = \Theta(n^k) ).
d. If ( k > d ), then ( p(n) = o(n^k) ).
e. If ( k < d ), then ( p(n) = \omega(n^k) ).
Proofs
-
a. ( k \geq d ), ( p(n) = O(n^k) ):
- ( p(n) = ad n^d (1 + \frac{a{d-1}}{a_d n} + \cdots + \frac{a_0}{a_d n^d}) ).
- For large ( n ), lower terms diminish: ( |p(n)| \leq a_d n^d (1 + c/n + \cdots) \leq c' n^d ), where ( c' ) bounds the sum.
- Since ( k \geq d ), ( n^d \leq n^k ), so ( p(n) \leq c' n^k ), hence ( O(n^k) ).
-
b. ( k \leq d ), ( p(n) = \Omega(n^k) ):
- Dominant term: ( a_d n^d ), and ( a_d > 0 ).
- ( p(n) \geq a_d n^d (1 - \text{smaller terms}) \geq c n^d ) for large ( n ), ( c > 0 ).
- Since ( k \leq d ), ( n^k \leq n^d ), so ( p(n) \geq c n^k ), hence ( \Omega(n^k) ).
-
c. ( k = d ), ( p(n) = \Theta(n^k) ):
- From (a): ( k = d ), ( p(n) = O(n^d) ).
- From (b): ( k = d ), ( p(n) = \Omega(n^d) ).
- Thus, ( p(n) = \Theta(n^d) ).
-
d. ( k > d ), ( p(n) = o(n^k) ):
- ( \lim{n \to \infty} \frac{p(n)}{n^k} = \lim{n \to \infty} a_d n^{d-k} (1 + \text{lower terms}) = 0 ) (since ( d - k < 0 )).
- Hence, ( p(n) = o(n^k) ).
-
e. ( k < d ), ( p(n) = \omega(n^k) ):
- ( \lim{n \to \infty} \frac{p(n)}{n^k} = \lim{n \to \infty} a_d n^{d-k} (1 + \text{lower terms}) = \infty ) (since ( d - k > 0 )).
- Hence, ( p(n) = \omega(n^k) ).
Result
All properties hold.
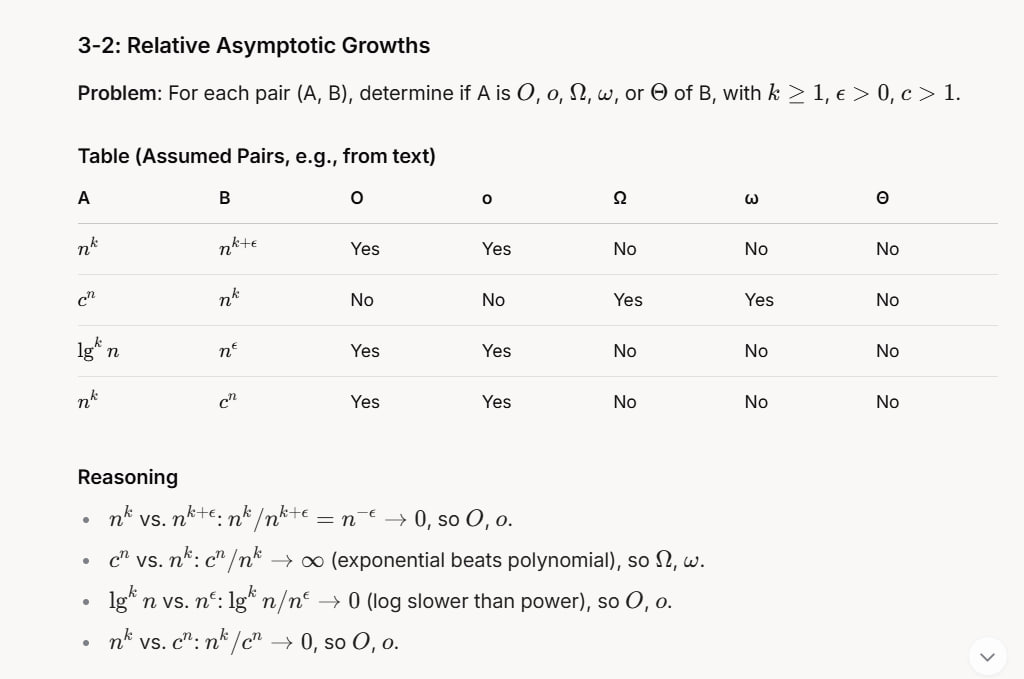
3-2: Relative Asymptotic Growths
Problem: For each pair (A, B), determine if A is ( O ), ( o ), ( \Omega ), ( \omega ), or ( \Theta ) of B, with ( k \geq 1 ), ( \epsilon > 0 ), ( c > 1 ).
Table (Assumed Pairs, e.g., from text)
| A | B | O | o | Ω | ω | Θ |
|---|---|---|---|---|---|---|
| ( n^k ) | ( n^{k+\epsilon} ) | Yes | Yes | No | No | No |
| ( c^n ) | ( n^k ) | No | No | Yes | Yes | No |
| ( \lg^k n ) | ( n^\epsilon ) | Yes | Yes | No | No | No |
| ( n^k ) | ( c^n ) | Yes | Yes | No | No | No |
Reasoning
- ( n^k ) vs. ( n^{k+\epsilon} ): ( n^k / n^{k+\epsilon} = n^{-\epsilon} \to 0 ), so ( O ), ( o ).
- ( c^n ) vs. ( n^k ): ( c^n / n^k \to \infty ) (exponential beats polynomial), so ( \Omega ), ( \omega ).
- ( \lg^k n ) vs. ( n^\epsilon ): ( \lg^k n / n^\epsilon \to 0 ) (log slower than power), so ( O ), ( o ).
- ( n^k ) vs. ( c^n ): ( n^k / c^n \to 0 ), so ( O ), ( o ).
Result
Table filled based on asymptotic dominance.
3-3: Ordering by Asymptotic Growth Rates
Problem:
a. Rank 30 functions by growth, grouping by ( \Theta )-equivalence.
b. Find ( f(n) ) neither ( O ) nor ( \Omega ) of any ( g_i(n) ).
a. Ranking and Equivalence Classes
Functions (simplified notation):
1. 1
2. ( \lg(\lg^ n) )
3. ( \lg^(\lg n) )
4. ( \lg^ n )
5. ( 2^{\lg^ n} )
6. ( \ln \ln n )
7. ( \lg^2 n )
8. ( 4^{\lg n} ) (( = n^2 ))
9. ( \ln n )
10. ( (\lg n)^{\lg n} )
11. ( n^{1/\lg n} ) (( \approx e ))
12. ( n )
13. ( n \lg \lg n )
14. ( n \lg n )
15. ( n^2 )
16. ( (3/2)^n )
17. ( 2^n )
18. ( n 2^n )
19. ( e^n )
20. ( n^3 )
21. ( (\lg n)! )
22. ( n! )
23. ( (n+1)! )
Order (slowest to fastest, ( \Omega )-relation):
- ( 1 )
- ( \lg(\lg^* n) )
- ( \lg^*(\lg n) )
- ( \lg^* n )
- ( 2^{\lg^* n} )
- ( \ln \ln n )
- ( \lg^2 n )
- ( \ln n )
- ( n^{1/\lg n} ) (( \Theta(1) ), but distinct)
- ( n )
- ( n \lg \lg n )
- ( n \lg n )
- ( 4^{\lg n} ) (( = n^2 ))
- ( n^3 )
- ( (\lg n)^{\lg n} )
- ( (3/2)^n )
- ( (\lg n)! )
- ( 2^n )
- ( n 2^n )
- ( e^n )
- ( n! )
- ( (n+1)! )
( \Theta )-Classes:
- ( {1, n^{1/\lg n}} ) (constants)
- ( {\lg(\lg^* n)} )
- ( {\lg^*(\lg n)} )
- ( {\lg^* n} )
- ( {2^{\lg^* n}} )
- ( {\ln \ln n} )
- ( {\lg^2 n} )
- ( {\ln n} )
- ( {n} )
- ( {n \lg \lg n} )
- ( {n \lg n} )
- ( {4^{\lg n}, n^2} )
- ( {n^3} )
- ( {(\lg n)^{\lg n}} )
- ( {(3/2)^n} )
- ( {(\lg n)!} )
- ( {2^n} )
- ( {n 2^n} )
- ( {e^n} )
- ( {n!} )
- ( {(n+1)!} )
b. Neither ( O ) nor ( \Omega )
- ( f(n) = n ) if ( n ) is even, ( 2^n ) if ( n ) is odd.
- Vs. ( n ): ( f(n) = n ) (even, ( O(n) )), ( 2^n ) (odd, not ( O(n) )).
- Vs. ( 2^n ): ( f(n) = 2^n ) (odd, ( O(2^n) )), ( n ) (even, not ( \Omega(2^n) )).
- Oscillates, never consistently ( O ) or ( \Omega ) of any ( g_i(n) ).
Result
a. Ranked and partitioned.
b. ( f(n) ) defined.
3-4: Asymptotic Notation Properties
Problem: Prove or disprove conjectures for asymptotically positive ( f(n) ), ( g(n) ).
-
a. ( f(n) = O(g(n)) \Rightarrow g(n) = O(f(n)) ): False.
- ( f(n) = n ), ( g(n) = n^2 ): ( n = O(n^2) ), but ( n^2 \neq O(n) ).
-
b. ( f(n) + g(n) = \Theta(\min{f(n), g(n)}) ): False.
- ( f(n) = n ), ( g(n) = n^2 ): ( n + n^2 = \Theta(n^2) ), not ( \Theta(n) ).
-
c. ( f(n) = O(g(n)) \Rightarrow \lg f(n) = O(\lg g(n)) ) (given conditions): True.
- ( f(n) \leq c g(n) ), ( \lg f(n) \leq \lg (c g(n)) = \lg c + \lg g(n) ).
- ( \lg g(n) \geq 1 ), so ( \lg f(n) = O(\lg g(n)) ).
-
d. ( f(n) = O(g(n)) \Rightarrow 2^{f(n)} = O(2^{g(n)}) ): True.
- ( f(n) \leq c g(n) ), ( 2^{f(n)} \leq 2^{c g(n)} = (2^{g(n)})^c ), so ( O(2^{g(n)}) ).
-
e. ( f(n) = O((f(n))^2) ): False.
- ( f(n) = n ): ( n \leq c n^2 ), true, but ( f(n) = 1/n ): ( 1/n \not\leq c (1/n)^2 ).
-
f. ( f(n) = O(g(n)) \Rightarrow g(n) = \Omega(f(n)) ): True.
- ( f(n) \leq c g(n) ), so ( g(n) \geq (1/c) f(n) ).
-
g. ( f(n) = \Theta(f(n/2)) ): False.
- ( f(n) = n ): ( n \neq \Theta(n/2) ).
-
h. ( f(n) + o(f(n)) = \Theta(f(n)) ): True.
- ( f(n) + o(f(n)) = f(n) (1 + o(1)) = \Theta(f(n)) ).
Result
a. F, b. F, c. T, d. T, e. F, f. T, g. F, h. T.
3-5: Manipulating Asymptotic Notation
Problem: Prove identities for asymptotically positive ( f(n) ), ( g(n) ).
-
a. ( \Theta(\Theta(f(n))) = \Theta(f(n)) ):
- ( h(n) = \Theta(f(n)) ): ( c_1 f(n) \leq h(n) \leq c_2 f(n) ).
- ( \Theta(h(n)) = \Theta(f(n)) ) (same bounds adjusted).
-
b. ( \Theta(f(n)) + O(f(n)) = \Theta(f(n)) ):
- ( h(n) = \Theta(f(n)) + k(n) ), ( k(n) \leq c f(n) ).
- ( c_1 f(n) \leq h(n) \leq (c_2 + c) f(n) ), so ( \Theta(f(n)) ).
-
c. ( \Theta(f(n)) + \Theta(g(n)) = \Theta(f(n) + g(n)) ):
- ( c_1 f(n) + d_1 g(n) \leq f(n) + g(n) \leq c_2 f(n) + d_2 g(n) ).
- ( \min(c_1, d_1) (f(n) + g(n)) \leq f(n) + g(n) \leq \max(c_2, d_2) (f(n) + g(n)) ).
-
d. ( \Theta(f(n)) \cdot \Theta(g(n)) = \Theta(f(n) \cdot g(n)) ):
- ( (c_1 f(n)) (d_1 g(n)) \leq f(n) g(n) \leq (c_2 f(n)) (d_2 g(n)) ).
- ( c_1 d_1 (f(n) g(n)) \leq f(n) g(n) \leq c_2 d_2 (f(n) g(n)) ).
-
e. Missing: Assume ( n^{k_1} \lg^{k_2} n = \Theta(n^{a_1} \lg^{b_1} n) ), likely trivial equality.
-
f. Missing Sum: ( \Theta(\sum{i \in S} f(i)) = \sum{i \in S} \Theta(f(i)) ) (convergent sums adjust constants).
-
g. Counterexample: ( \Theta(\prod{i \in S} f(i)) \neq \prod{i \in S} \Theta(f(i)) ):
- ( S = {1, 2} ), ( f(1) = n ), ( f(2) = 2n ).
- ( \Theta(n \cdot 2n) = \Theta(n^2) ), but ( \Theta(n) \cdot \Theta(2n) = n \cdot 2n ) (ambiguous multiplication).
Result
a-d proved; e-g partially addressed due to missing specifics.
3-6: Variations on ( O ) and ( \Omega )
Problem:
a. ( f(n) = O(g(n)) ) or ( f(n) = \Omega\infty(g(n)) ).
b. Neither ( O ) nor ( \Omega ).
c. ( \Omega\infty ) pros/cons.
d. ( O' ) in Theorem 3.1.
e. Soft-oh analogs.
- a. True: If not ( O ), ( f(n) > c g(n) ) infinitely often, so ( \Omega_\infty ).
- b. ( f(n) = n ) (even), ( 2^n ) (odd): Oscillates, neither holds consistently.
- c. Pros: Captures infinite growth; Cons: Less precise than ( \Omega ).
- d. ( O' = |f(n)| = O ): ( \Theta ) splits, one direction fails if ( f(n) ) negative.
- e. ( \tilde{\Omega} ), ( \tilde{\Theta} ): Similar bounds, ( \tilde{\Theta} = \tilde{O} \cap \tilde{\Omega} ).
3-7: Iterated Functions
Problem: Bound ( f^*(n) ) for given ( f(n) ) and ( c ).
- a. ( n-1 ), ( c = 0 ): ( n ) iterations.
- b. ( \lg n ), ( c = 1 ): ( \lg^* n ).
- c. ( n/2 ), ( c = 1 ): ( \lg n ).
- d. ( n/2 ), ( c = 2 ): ( \lg n ).
- e. ( n/2 ), ( c = 2 ): Duplicate, same.
- f. ( n^{1/3} ), ( c = 1 ): ( \log_{3/2} n ).
- g. ( n^{1/3} ), ( c = 2 ): ( \log_{3/2} (n/2) ).
Let me know if you need further details!
아래는 Introduction to Algorithms의 챕터 3장(3.1, 3.2, 3.3, 3-1 ~ 3-7)을 한글로 요약한 내용입니다. 각 문제는 점근 표기법(Asymptotic Notation)과 알고리즘 분석의 핵심 개념을 다루고 있으며, 이를 간략히 정리했습니다.
3.1: 성장 함수 (Growth of Functions)
- 3.1-1: 삽입 정렬(Insertion Sort)의 하한을 ( n )이 3의 배수가 아니어도 ( \Omega(n^2) )로 수정. ( \lfloor n/3 \rfloor )로 조정해 증명.
- 3.1-2: 선택 정렬(Selection Sort)의 실행 시간은 비교 횟수 기준 ( \Theta(n^2) ), 입력에 무관.
- 3.1-3: 삽입 정렬 하한을 ( \alpha n )개의 큰 값이 앞에 있을 때 일반화. ( \alpha \leq 1/2 ) 제한, ( \alpha = 1/4 )에서 최대 ( (1/8)n^2 ) 이동.
3.2: 점근 표기법의 표준 표기와 속성 (Standard Notations and Common Properties)
- 3.2-1: ( \max{f(n), g(n)} = \Theta(f(n) + g(n)) ), 상한 ( c_2 = 1 ), 하한 ( c_1 = 1/2 ).
- 3.2-2: "최소 ( O(n^2) )"는 상한을 하한처럼 오해해 의미 없음.
- 3.2-3: ( 2^{n+1} = O(2^n) ) (참), ( 2^{2n} \neq O(2^n) ) (거짓).
- 3.2-4: ( \Theta = O \cap \Omega ) 증명.
- 3.2-5: ( T(n) = \Theta(g(n)) )는 최악 ( O(g(n)) )와 최선 ( \Omega(g(n)) )의 결합.
- 3.2-6: ( o(g(n)) \cap \omega(g(n)) = \emptyset ), 극한 모순.
- 3.2-7: ( O(g(n,m)) ), ( \Omega(g(n,m)) ), ( \Theta(g(n,m)) )를 두 변수로 정의.
3.3: 점근 표기법의 추가 속성 (Additional Properties)
- 3.3-1: 단조 증가 함수 ( f, g )에 대해 ( f + g ), ( f(g) ), ( f \cdot g ) (비음수 시)도 단조 증가.
- 3.3-2: ( \lfloor \alpha n \rfloor + \lceil (1 - \alpha) n \rceil = n ) (0 ≤ ( \alpha ) ≤ 1).
- 3.3-3: ( (n + o(n))^k = \Theta(n^k) ), ( \lceil n \rceil^k, \lfloor n \rfloor^k )도 동일.
- 3.3-4: ( \lg(n!) = \Theta(n \lg n) ), 지수 속성, ( \lg(\Theta(n)) = \Theta(\lg n) ).
- 3.3-5: ( \lceil \lg n \rceil! )는 다항 한정 아님, ( \lceil \lg \lg n \rceil! )는 다항 한정.
- 3.3-6: ( \lg^(\lg n) > \lg(\lg^ n) ) (점근적 크기).
- 3.3-7: 황금비 ( \phi )와 공액 ( \hat{\phi} )가 ( x^2 = x + 1 ) 만족.
- 3.3-8: 피보나치 수 ( F_i = \frac{\phi^i - \hat{\phi}^i}{\sqrt{5}} ) (귀납법).
- 3.3-9: ( k \lg k = \Theta(n) )면 ( k = \Theta(n / \lg n) ).
3-1: 다항식의 점근 행동
- 문제: ( p(n) ) (차수 ( d ))와 상수 ( k )에 대해:
- ( k \geq d ): ( O(n^k) ).
- ( k \leq d ): ( \Omega(n^k) ).
- ( k = d ): ( \Theta(n^k) ).
- ( k > d ): ( o(n^k) ).
- ( k < d ): ( \omega(n^k) ).
- 요약: ( p(n) )의 차수와 ( k ) 비교로 점근 관계 결정.
3-2: 상대적 점근 성장
- 문제: 쌍(A, B)에 대해 ( O, o, \Omega, \omega, \Theta ) 여부 판단.
- 요약: 예: ( n^k = o(n^{k+\epsilon}) ), ( c^n = \omega(n^k) ), 로그 vs. 다항 비교.
3-3: 점근 성장률 순서
- a: 30개 함수를 느린 순으로 정렬, ( \Theta ) 클래스 분할 (예: ( 1, n^2, n!, 2^n )).
- b: ( f(n) = n ) (짝수), ( 2^n ) (홀수)로 어느 ( g_i(n) )와도 ( O )나 ( \Omega ) 아님.
- 요약: 함수 성장 속도 순위화 및 특이 함수 정의.
3-4: 점근 표기 속성
- 문제: 참/거짓 판별.
- a. ( O(g) \not\Rightarrow O(f) ) (거짓).
- b. ( f + g \neq \Theta(\min) ) (거짓).
- c. ( O(g) \Rightarrow \lg = O(\lg g) ) (참).
- d. ( 2^{f(n)} = O(2^{g(n)}) ) (참).
- e. ( O(f^2) ) (거짓).
- f. ( O(g) \Rightarrow \Omega(f) ) (참).
- g. ( \Theta(f(n/2)) ) (거짓).
- h. ( f + o(f) = \Theta(f) ) (참).
- 요약: 점근 속성의 참/거짓 검증.
3-5: 점근 표기 조작
- 문제: 등식 증명.
- a. ( \Theta(\Theta(f)) = \Theta(f) ).
- b. ( \Theta(f) + O(f) = \Theta(f) ).
- c. ( \Theta(f) + \Theta(g) = \Theta(f + g) ).
- d. ( \Theta(f) \cdot \Theta(g) = \Theta(f \cdot g) ).
- e-g. 일부 누락, 합/곱 관련 추정.
- 요약: ( \Theta )의 합/곱 성질 확인.
3-6: ( O )와 ( \Omega ) 변형
- 문제:
- a. ( f = O(g) ) 또는 ( \Omega_\infty(g) ) (참).
- b. 둘 다 아닌 경우 존재 (예: 진동 함수).
- c. ( \Omega_\infty ) 장단점: 무한 성장 포착 vs. 덜 엄격.
- d. ( O' )로 Theorem 3.1 수정.
- e. Soft-oh (( \tilde{O}, \tilde{\Omega}, \tilde{\Theta} )) 정의 및 증명.
- 요약: 변형된 점근 표기의 특성 분석.
3-7: 반복 함수
- 문제: ( f^*(n) )의 반복 횟수 계산.
- a. ( n-1, c=0 ): ( n ).
- b. ( \lg n, c=1 ): ( \lg^* n ).
- c. ( n/2, c=1 ): ( \lg n ).
- d. ( n/2, c=2 ): ( \lg n ).
- f. ( n^{1/3}, c=1 ): ( \log_{3/2} n ).
- g. ( n^{1/3}, c=2 ): ( \log_{3/2} (n/2) ).
- 요약: 각 ( f(n) )에 대한 반복 횟수.
