BFS - 너비 우선 탐색

BFS (Breadth-first-search)는 루트 노드 또는 임의 노드에서 인접한 노드들을 먼저 탐색하는 방법

큐를 통해서 구현한다. (해당 노드의 주변부터 탐색해야하기 때문이다.)

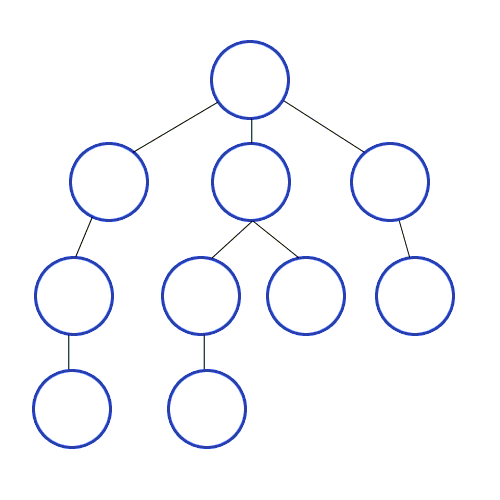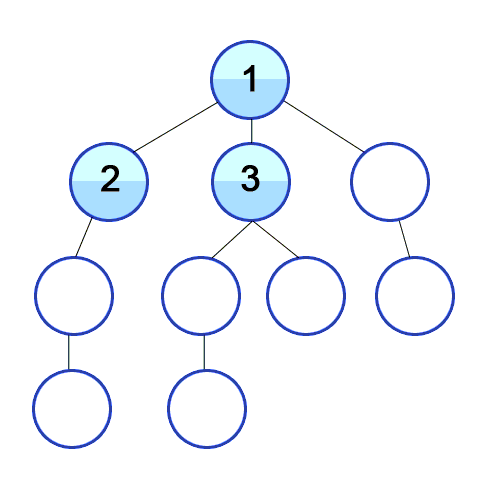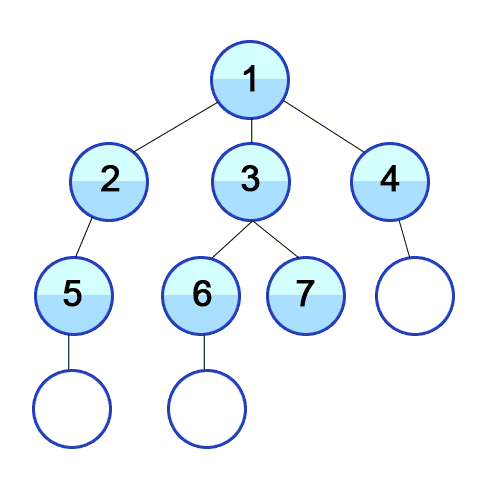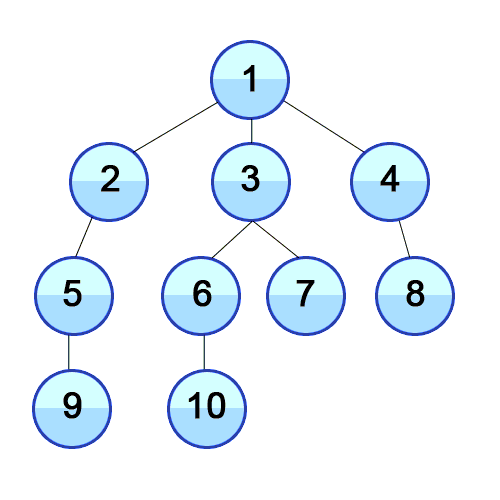
특징

• 두개의 큐를 사용한다.
• 출발 노드에서 목표 노드까지의 최단 길이 경로를 보장한다
• 최소 비용 (즉, 모든 곳을 탐색하는 것보다 최소 비용이 우선일 때 적합하다.)

시간 복잡도

• 인접 행렬 : O(V^2)
• 인접 리스트 : O(V + E)
  접점(V), 간선(E)

BFS로 효과적으로 풀 수 있는 문제의 조건

1. 최소 비용 문제
2. 간선의 가중치가 1이다.
3. 정점과 간선의 개수가 적다. (시간 제약, 메모리 제한 내에 만족)

구현

const graph = {
    1: [2,3,4],
    2: [1,5],
    3: [1,6,7],
    4: [1,8],
    5: [2,9],
    6: [3,10],
    7: [3],
    8: [4],
    9: [5],
    10: [6],
};

const BFS = (graph, n) => {
    const visited = [];
    let needVisit = [];

    needVisit.push(n);
    while(needVisit.length){
        const node = needVisit.shift();
        if(!visited.includes(node)) {
            visited.push(node);
            needVisit = [...needVisit, ...graph[node]];
        }
    }
    return visited;
}
BFS(graph, 1);
//[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

---

DFS - 깊이 우선 탐색

DFS (Depth-first-Search)는 루트 노드 혹은 임의 노드에서 다음 브렌치로 넘어가기 전에, 해당 브렌치를 모두 탐색하는 방법

스택 or 재귀함수를 통해 구현한다.

특징

• 한 개의 큐와 한 개의 스택을 사용한다.
• 저장 공간의 수요가 비교적 적다.
• 목표 노드가 깊은 단계에 있을 경우 빨리 구할 수 있다.
• BFS보다 속도가 느릴 수 있으며, 보통 경로가 존재하는지를 판별할 때 사용한다.

시간 복잡도

• 인접 행렬 : O(V^2)
• 인접 리스트 : O(V + E)
  접점(V), 간선(E)

구현

const graph = {
    1: [2,3,4],
    2: [1,5],
    3: [1,6,7],
    4: [1,8],
    5: [2,9],
    6: [3,10],
    7: [3],
    8: [4],
    9: [5],
    10: [6],
};

const DFS = (graph, n) => {
    const visited = [];
    let needVisit = [];

    needVisit.push(n);
    while(needVisit.length){
        const node = needVisit.pop();
        if(!visited.includes(node)) {
            visited.push(node);
          // 내림차순 정렬을 해주면 좌측부터 탐색하고 오름차순 정렬을 하면 우측부터 탐색
            graph[node].sort((a,b) => b - a); 
            needVisit = [...needVisit, ...graph[node]];
        }
    }
    return visited;
}
DFS(graph, 1);
// [1, 2, 5, 6, 3, 6, 10, 7, 4, 8]

참고

• [알고리즘] 그래프 탐색 알고리즘 by javascript - BFS(너비 우선 탐색), DFS(깊이 우선 탐색)
• Tech Interview - DFS & BFS