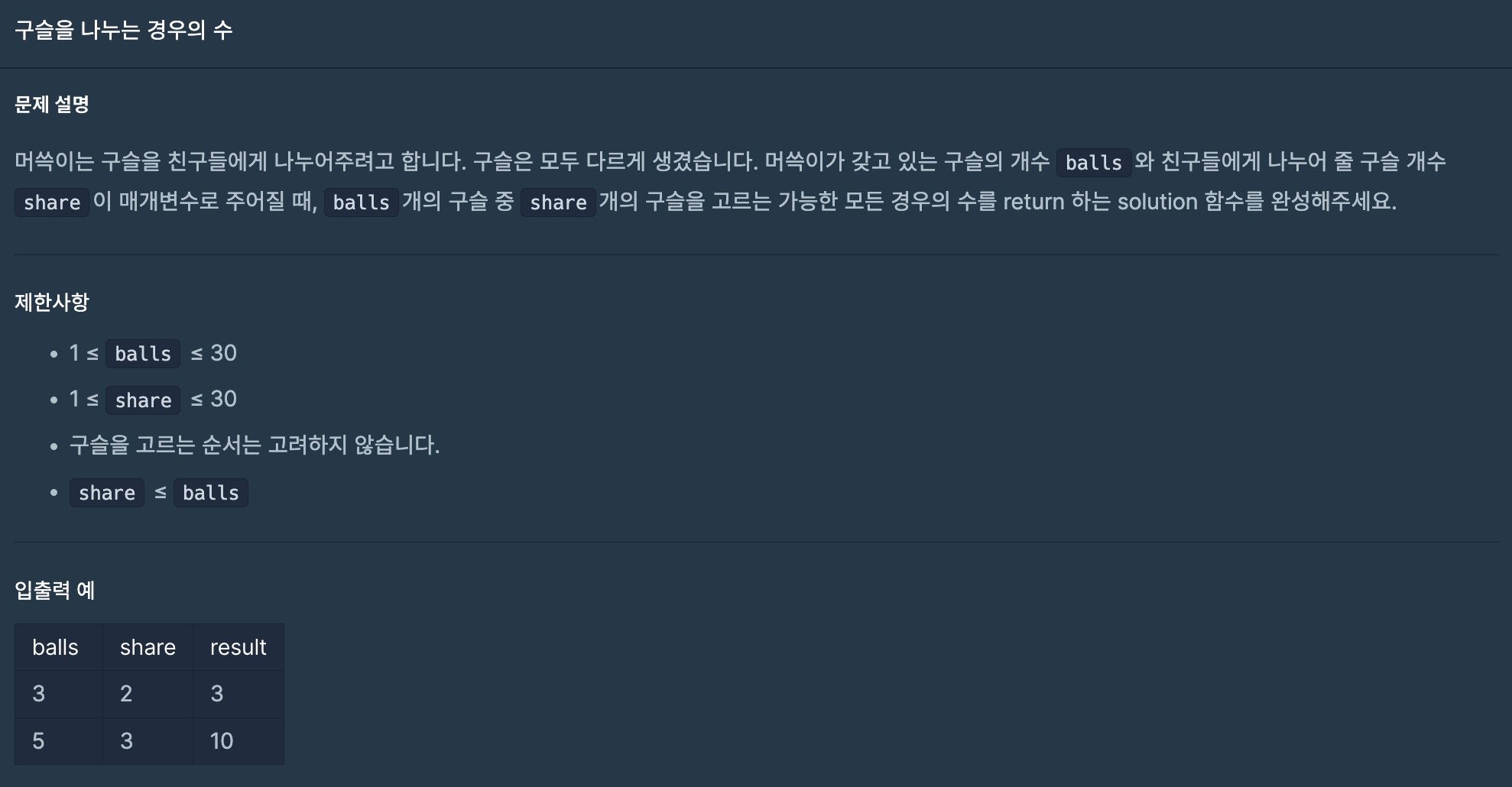
< 오늘의 문제 >
const fac = (num) => num === 0 ? 1 : num * fac(num - 1);
function solution(balls, share) {
return Math.round(fac(balls) / fac(balls - share) / fac(share));
}-
나의 풀이
팩토리얼 함수 (fac):
fac 함수에 매개변수 num을 받는다.
삼항 연산자를 사용하여, num이 0일 경우 1을 반환. num이 0이 아니면, num * fac(num - 1)을 계산하여 반환.
재귀적으로 num이 0이 될 때까지 num을 감소시키면서 팩토리얼을 계산하는 방식.조합 계산 함수 (solution):
solution 함수는 두 매개변수 balls와 share를 받는다.
함수는 Math.round(fac(balls) / fac(balls - share) / fac(share))를 통해 조합의 수를 계산.
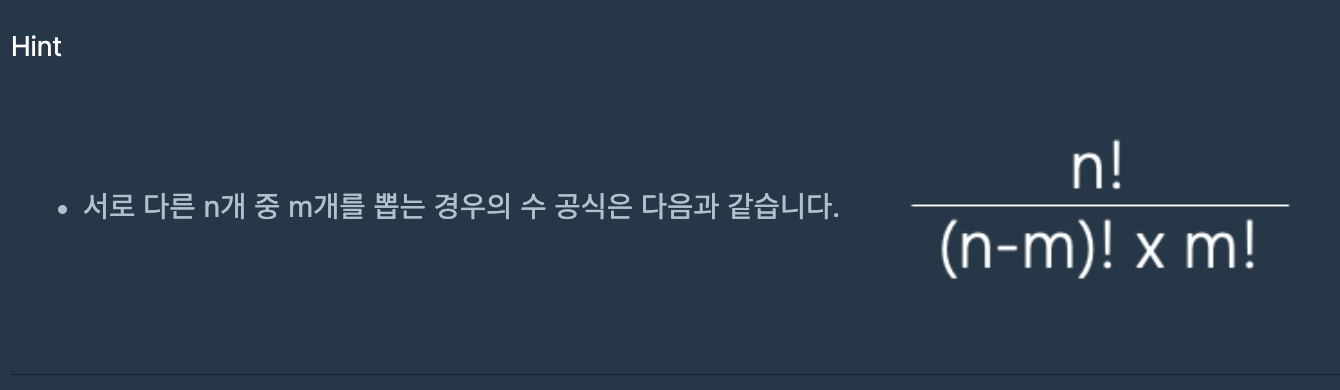
수학적 조합 공식 nCm = n! / ((n-m)! * m!)
fac(balls)는 전체 공의 수에 대한 팩토리얼을 계산하고, fac(balls - share)는 공을 공유하지 않을 때의 경우의 수에 대한 팩토리얼을 계산. fac(share)는 공유할 공의 수에 대한 팩토리얼을 계산.
마지막으로 Math.round 함수를 사용하여 결과를 반올림.
재귀(Recursion)는 컴퓨터 과학에서 어떤 함수가 직접 또는 간접적으로 자기 자신을 호출하는 프로그래밍 기법.
귀를 사용하면 복잡한 문제를 간단하고 우아한 방법으로 해결할 수 있으며, 주로 분할 정복 알고리즘, 탐색 알고리즘, 동적 프로그래밍 등 여러 분야에서 널리 사용된다.
재귀 함수의 주요 특징은 다음과 같다:
기저 조건(Base Case): 재귀 함수는 종료 조건을 가지고 있어야 한다.
이 조건에 도달하면 더 이상 자기 자신을 호출하지 않고 종료.
자기 호출(Self-Call): 함수는 주어진 문제를 해결하기 위해 자기 자신을 호출.
이 과정에서 문제의 크기를 줄여가며, 결국 기저 조건에 도달할 수 있도록 한다.
재귀 함수는 반복문으로 풀 수 있는 문제들을 간결하게 표현할 수 있지만, 함수 호출에 따른 오버헤드가 있으며, 잘못 설계된 경우 스택 오버플로우를 일으킬 수 있다. 따라서 재귀 함수를 사용할 때는 기저 조건과 효율성을 고려하여 신중하게 설계해야 한다.