[BaekJoon] 9461 파도반 수열

1.  문제 링크

https://www.acmicpc.net/problem/9461

2.  문제

요약

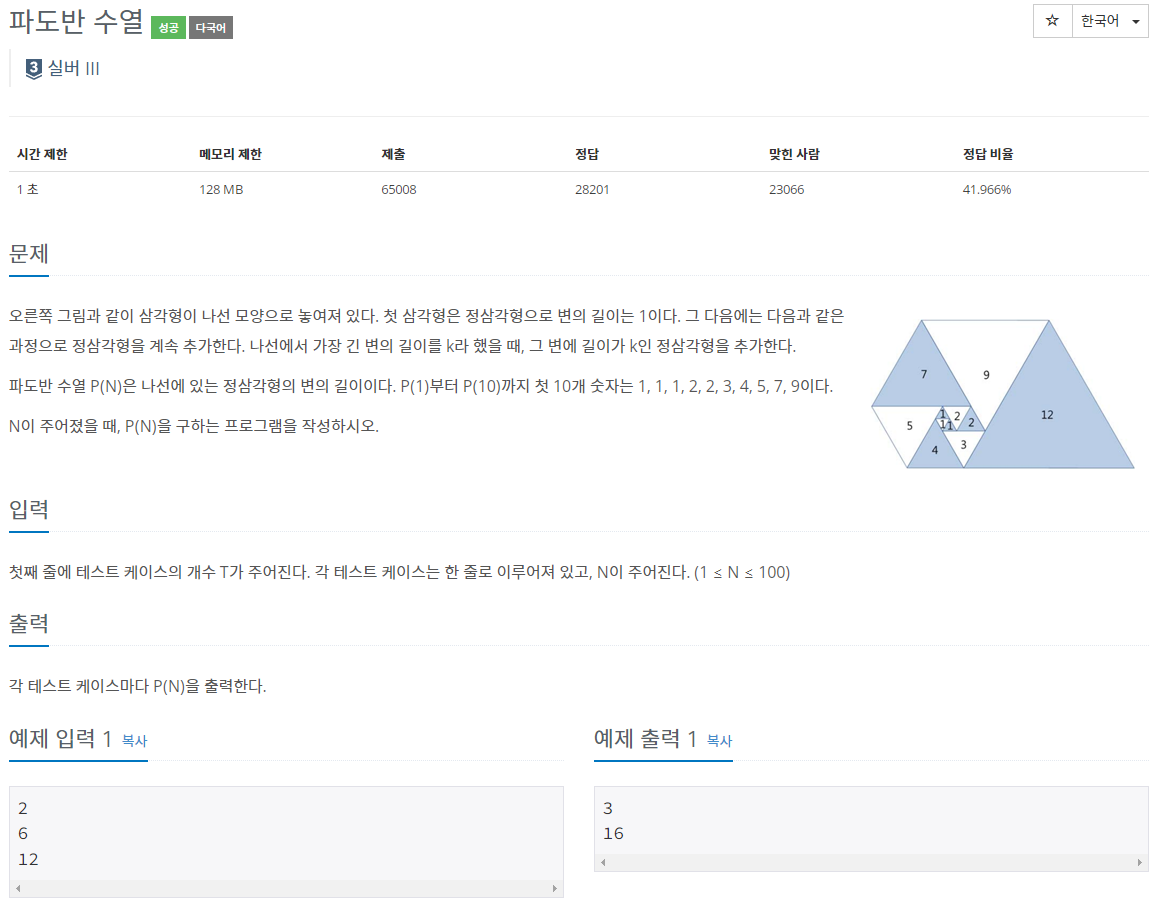
• 삼각형이 나선 모양으로 놓이고 첫 번째 삼각형은 정삼각형으로 변의 길이가 1입니다.
• 이후에 정삼각형을 계속 추가해나가는데, 나선에서 가장 긴 변의 길이 k를 한 변의 길이로 하는 정삼각형을 추가해나갑니다.
• 파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이를 나타내는데, N이 주어졌을 때 P(N)을 구하는 문제입니다.
• 입력: 첫 번째 줄에 테스트 케이스의 개수 T가 주어지고 두 번째 줄부터 T개의 줄에는 1보다 크거나 같고 100보다 작거나 같은 N이 주어집니다.
• 출력: 첫 번째 줄부터 T개의 줄에 테스트 케이스 순서대로 P(N)을 출력합니다.

3.  소스코드

Top-Down 방식

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main {
	Long[] dp;
    public long findWaveHalfSeq(int n) {
		if(dp[n] == null) {
			dp[n] = findWaveHalfSeq(n - 1) + findWaveHalfSeq(n - 5);
		}
		return dp[n];
	}
	
	public long[] getWaveHalfSeq(int[] nums) {
		dp = new Long[101];
		dp[0] = 0L;
		dp[1] = 1L;
		dp[2] = 1L;
		dp[3] = 1L;
		dp[4] = 2L;
		dp[5] = 2L;
		long[] result = new long[nums.length];
		for(int i = 0; i < nums.length; i++) {
			result[i] = findWaveHalfSeq(nums[i]);
		}
		return result;
	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		int test_num = Integer.parseInt(br.readLine());
		int[] nums = new int[test_num];
		for(int i = 0; i < nums.length; i++) {
			nums[i] = Integer.parseInt(br.readLine());
		}
		br.close();
		Main m = new Main();
		long[] result = m.getWaveHalfSeq(nums);
		for(int i = 0; i < result.length; i++) {
			bw.write(result[i] + "\n");
		}
		bw.flush();
		bw.close();
	}
}

Bottom-Up 방식

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main {
	public long[] getWaveHalfSeq(int[] nums) {
		long[] result = new long[nums.length];
		for(int i = 0; i < nums.length; i++) {
			if(1 <= nums[i] && nums[i] <= 3) {
				result[i] = 1;
				continue;
			} else if(4 <= nums[i] && nums[i] <= 5) {
				result[i] = 2;
				continue;
			}
			long[] dp = new long[nums[i] + 1];
			dp[1] = 1L;
			dp[2] = 1L;
			dp[3] = 1L;
			dp[4] = 2L;
			dp[5] = 2L;
			for(int j = 6; j <= nums[i]; j++) {
				dp[j] = dp[j - 5] + dp[j - 1];
			}
			result[i] = dp[nums[i]];
		}
		return result;
	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		int test_num = Integer.parseInt(br.readLine());
		int[] nums = new int[test_num];
		for(int i = 0; i < nums.length; i++) {
			nums[i] = Integer.parseInt(br.readLine());
		}
		br.close();
		Main m = new Main();
		long[] result = m.getWaveHalfSeq(nums);
		for(int i = 0; i < result.length; i++) {
			bw.write(result[i] + "\n");
		}
		bw.flush();
		bw.close();
	}
}

4.  접근

• 해당 문제는 DP를 이용하여 해결할 수 있습니다.
• DP는 재귀함수를 사용하는 Top-Down 방식과 반복문을 사용하는 Bottom-Up 방식이 존재하고 두 방식으로 풀이해보았습니다.

Top-Down 방식

• 첫 세 개의 삼각형은 한 변이 1인 정삼각형으로 이루어져 있고, 이후 두 개의 삼각형은 한 변이 2인 정삼각형으로 이루어져 있습니다.
• 그 이후부터의 정삼각형의 한 변의 길이는 이전 두 삼각형의 변의 길이를 합과 같은데, 문제의 그림에서 확인해보면 현재 정삼각형의 바로 이전 정삼각형의 한 변의 길이와 5개 이전의 정삼각형의 한 변의 길이의 합이 현재 정삼각형의 한 변의 길이와 같습니다.

public long findWaveHalfSeq(int n) {
	if(dp[n] == null) {
		dp[n] = findWaveHalfSeq(n - 1) + findWaveHalfSeq(n - 5);
	}
	return dp[n];
}

• 위 점화식을 바탕으로 P(N)을 구합니다.

1. P(N)의 값을 저장할 배열 dp를 생성하고 앞 5개의 값을 초기화시킵니다.

2. 각 테스트 케이스에서 재귀함수를 통하여 P(N)을 구합니다.

   • dp 배열에 아직 값이 설정된 적이 없다면 위에서 구한 점화식을 통해 n에서의 정삼각형의 한 변의 길이를 구합니다.

3. 2번의 재귀함수를 통해 구한 P(N)을 출력합니다.

Bottom-Up 방식

• Top-down 방식에서 구한 점화식을 바탕으로 재귀함수를 반복문으로 변경합니다.
• 첫 5개의 값은 초기화시키고, n번째 정삼각형의 한 변의 길이가 바로 이전 정삼각형의 한 변의 길이와 5개 이전의 정삼각형의 한 변의 길이의 합이므로 초기화되지 않은 6부터 n까지 반복문을 돌면서 위에서 구한 점화식을 바탕으로 P(N)을 구합니다.

for(int i = 3; i < dp.length; i++) {
	dp[i] = Math.max(dp[i - 2], dp[i - 3] + size[i - 1]) + size[i];
}

• 하지만 마지막 dp의 값이 항상 최댓값이 아니기 때문에 위에서 구한 값을 바로 이전 잔에서의 최대로 마실 수 있는 양과 비교하여 더 많은 양으로 현재 잔에서의 최대로 마실 수 있는 양을 갱신합니다.

for(int j = 6; j <= nums[i]; j++) {
	dp[j] = dp[j - 5] + dp[j - 1];
}