[BaekJoon] 1059 좋은 구간

1.  문제 링크

2.  문제

요약

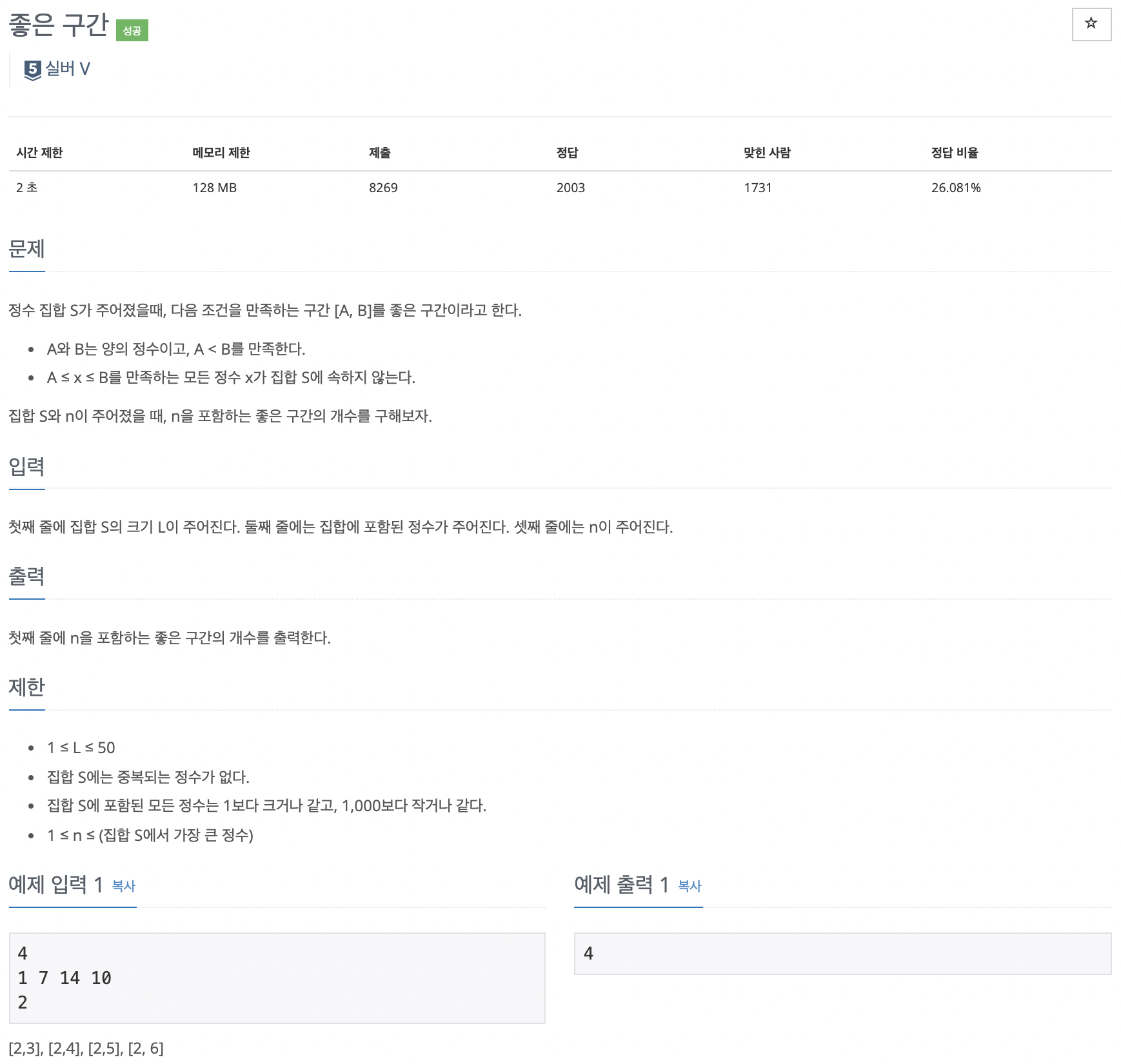
• 정수 집합에 대해서 A보다 크거나 같고 B보다 작거나 같은 모든 정수들이 정수 집합에 속하지 않는 구간 [A,B]를 좋은 구간이라고 합니다.
• 입력: 첫째 줄에는 정수 집합의 크기가 주어지고 둘째 줄에는 집합의 원소들이 주어지며 셋째 줄에는 좋은 구간에 포함되어야 할 숫자를 입력합니다.
• 출력: 좋은 구간에 포함되어야 할 숫자를 포함하는 좋은 구간의 개수를 출력합니다.

3.  소스코드

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    public int goodRange(Integer[] elem, int n) {
		if(Arrays.asList(elem).contains(n)) {
			return 0;
		} else {
            if(n < elem[0]) {
                int total = 0;
                for(int i = 1; i < n; i++) {
                    for(int j = n; j < elem[0]; j++){
                        total++;
                    }
                }
                for(int i = n + 1; i < elem[0]; i++)
                    total++;
                
                return total;
            }
            if(n > elem[elem.length - 1]) {
                int total = 0;
                for(int i = elem[elem.length - 1] + 1; i < n; i++) {
                    for(int j = n; j <= 1000; j++){
                        total++;
                    }
                }
                for(int i = n + 1; i <= 1000; i++)
                    total++;
                
                return total;
            }
            
			int index = -1;
			for(int i = 0; i < elem.length; i++) {
				if(n < elem[i]) {
					index = i;
					break;
				}
			}
			
			int total = 0;
			
			for(int i = elem[index - 1] + 1; i <= n; i++) {
				if(i == n) {
					for(int j = n + 1; j < elem[index]; j++) {
						total++;
					}
				}
				else {
					for(int j = n; j < elem[index]; j++) {
						total++;
					}
				}
			}
			
			return total;
		}
	}
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int size = sc.nextInt();
        Integer[] elem = new Integer[size];
        for(int i = 0; i < elem.length; i++) {
            elem[i] = sc.nextInt();
        }
        int n = sc.nextInt();
        Arrays.sort(elem);
        
        Main m = new Main();
        System.out.println(m.goodRange(elem, n));
    }
}

4.  접근

1. 주어진 정수 집합에 좋은 구간에 포함되어야 할 숫자가 포함되어 있는 경우
• 좋은 구간에 포함되는 정수는 주어진 정수 집합에 포함되어있지 않아야 하는데 좋은 구간에 포함되어야 할 정수가 이미 주어진 정수 집합에 포함되어있으므로 좋은 구간의 개수는 0입니다.
2. 좋은 구간에 포함되어야 할 정수가 주어진 정수 집합의 가장 작은 값보다 작을 경우
• 좋은 구간을 [A,B], 좋은 구간에 포함되어야 할 정수를 n이라고 한다면 A에는 1부터 n까지 가능하고 B는 n부터 정수 집합의 가장 작은 값 - 1까지 가능합니다.
• 처음 2중 for문은 A가 1부터 n - 1까지일 때의 좋은 구간의 개수를 구합니다.
• 두 번째 for문은 A가 n일 때의 좋은 구간의 개수를 구합니다.
• 이 두 개의 값을 더하면 전체 좋은 구간의 개수를 구할 수 있습니다.
3. 좋은 구간에 포함되어야 할 정수가 주어진 정수 집합의 가장 큰 값보다 클 경우
• 좋은 구간을 [A,B], 좋은 구간에 포함되어야 할 정수를 n이라고 한다면 A에는 정수 집합의 가장 큰 값 + 1부터 n까지 가능하고 B는 n부터 1000까지 가능합니다. 그 이유는 문제의 제한사항으로 가장 큰 수는 1000까지 가능하다고 제한을 두었기 때문입니다.
• 처음 2중 for문은 A가 주어진 정수 집합의 가장 큰 값 + 1부터 n - 1까지일 때의 좋은 구간의 개수를 구합니다.
• 두 번째 for문은 A가 n일 때의 좋은 구간의 개수를 구합니다.
• 이 두 개의 값을 더하면 전체 좋은 구간의 개수를 구할 수 있습니다.
4. 좋은 구간에 포함되어야 할 정수가 주어진 정수 집합 사이에 있을 경우
• 좋은 구간을 [A,B], 좋은 구간에 포함되어야 할 정수를 n이라고 한다면 A에는 n보다 작은 정수 집합의 가장 큰 값 + 1부터 n까지 가능하고 B는 n부터 n보다 큰 정수 집합의 가장 작은 값 - 1까지 가능합니다.
• 우선 정수 집합에서 n보다 큰 가장 작은 값의 index를 찾습니다.
• A가 n보다 작은 정수 집합의 가장 큰 값 + 1부터 n - 1일 때의 좋은 집합의 개수를 구하고 A가 n일 때의 좋은 집합의 개수를 구합니다.
• 이 두 개의 값을 더하면 전체 좋은 구간의 개수를 구할 수 있습니다.