Tree
트리는 정점(Node)과 선분(Branch)을 이용하여 사이클을 이루지 않도록 구성한 Graph의 특수한 형태이다. 트리는 가족의 계보, 회사 조직도, 히프등을 표현하기에 적합하다. 이러한 트리는 계층적 구조로, 한 방향이 아닌 여러 방향으로 뻗어 나갈 수 있으므로 '비선형구조'에 포함된다.
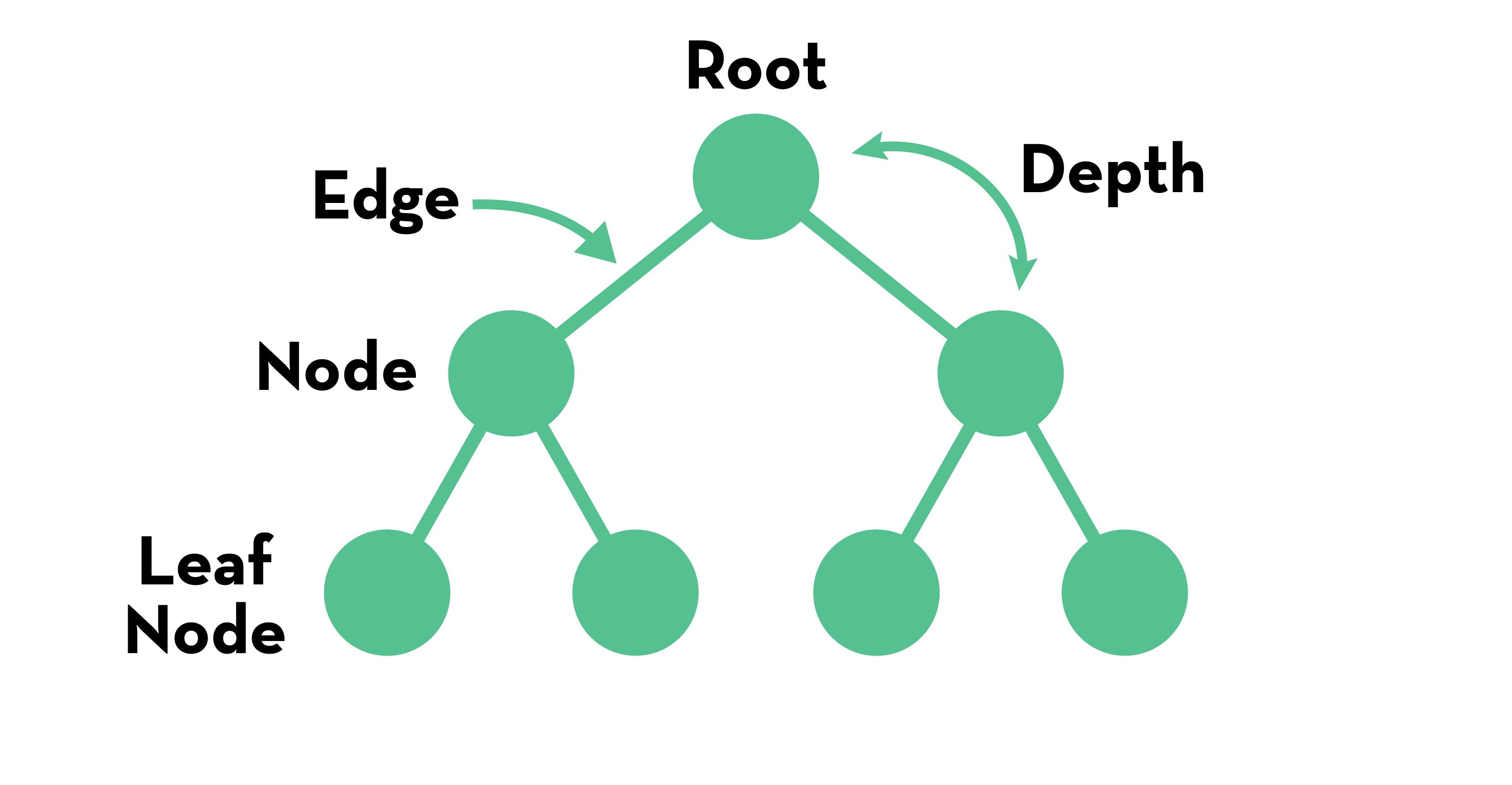
트리의 표현을 위한 용어는 다음과 같다.
- 노드(Node): 트리의 기본요소로 키나 값을 가지는 주체
- 루트(Root): 트리의 가장 상위에 있는 노드
- 엣지(Edge/Branch): 두 노드 사이의 링크
- 단말 노드(Terminal Node/leaf node/external node) : 자식이 하나도 없는 노드
- 내부 노드(internal node): 적어도 하나의 자식 노드가 존재하는 노드
- 레벨(Level): 노드와 노드 사이의 거리
- 높이(Height): 루트에서 가장 마지막 노드까지의 레벨
- 깊이(depth): 특정 노드에서 루트까지의 레벨
이진트리와 순회
트리 구조는 효율적인 탐색을 위해 사용되기도 하며, 이를 위한 트리가 바로 이진탐색트리(Binary Search Tree)이다.
보통 자식 노드가 최대 두 개인 노드들로 구성된 트리를 이진 트리라고 한다. 이 중 모든 왼쪽 자식들은 루트나 부모보다 작은 값이고, 모든 오른쪽 자식들은 루트나 부모보다 큰 값인 특징을 가진 트리가 바로 이진탐색트리이다.
이러한 트리에서 특정 값을 찾기 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회(traversal)라고 한다.
이진 트리의 순회 과정은 다음과 같이 나누어진다.
-
깊이 우선 순회 방법(Depth First Traversal)
전위 순회(Pre-order traversal): 루트 -> 왼쪽 -> 오른쪽
정위 순회(In-order traversal): 왼쪽 -> 루트 -> 오른쪽
후위 순회(Post-order traversal): 왼쪽 -> 오른쪽 -> 루트 -
너비 우선 순회 방법(Breadth First Traversal)
레벨 순회(Level-order traversal): 레벨 순, 동일 레벨에선 왼쪽 -> 오른쪽
참고
코딩팩토리 - 트리(Tree)구조란 무엇인가?
이진탐색트리(Binary Search Tree)
이진 트리(Binary Tree)와 트리 순회(Tree Traversal)
