문제

---

셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다.

양의 정수 n이 주어졌을 때, 이 수를 시작해서 n, d(n), d(d(n)), d(d(d(n))), ...과 같은 무한 수열을 만들 수 있다.

예를 들어, 33으로 시작한다면 다음 수는 33 + 3 + 3 = 39이고, 그 다음 수는 39 + 3 + 9 = 51, 다음 수는 51 + 5 + 1 = 57이다. 이런식으로 다음과 같은 수열을 만들 수 있다.

33, 39, 51, 57, 69, 84, 96, 111, 114, 120, 123, 129, 141, ...

n을 d(n)의 생성자라고 한다. 위의 수열에서 33은 39의 생성자이고, 39는 51의 생성자, 51은 57의 생성자이다. 생성자가 한 개보다 많은 경우도 있다. 예를 들어, 101은 생성자가 2개(91과 100) 있다.

생성자가 없는 숫자를 셀프 넘버라고 한다. 100보다 작은 셀프 넘버는 총 13개가 있다. 1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97

10000보다 작거나 같은 셀프 넘버를 한 줄에 하나씩 출력하는 프로그램을 작성하시오.

입력

---

입력은 없습니다.

출력

---

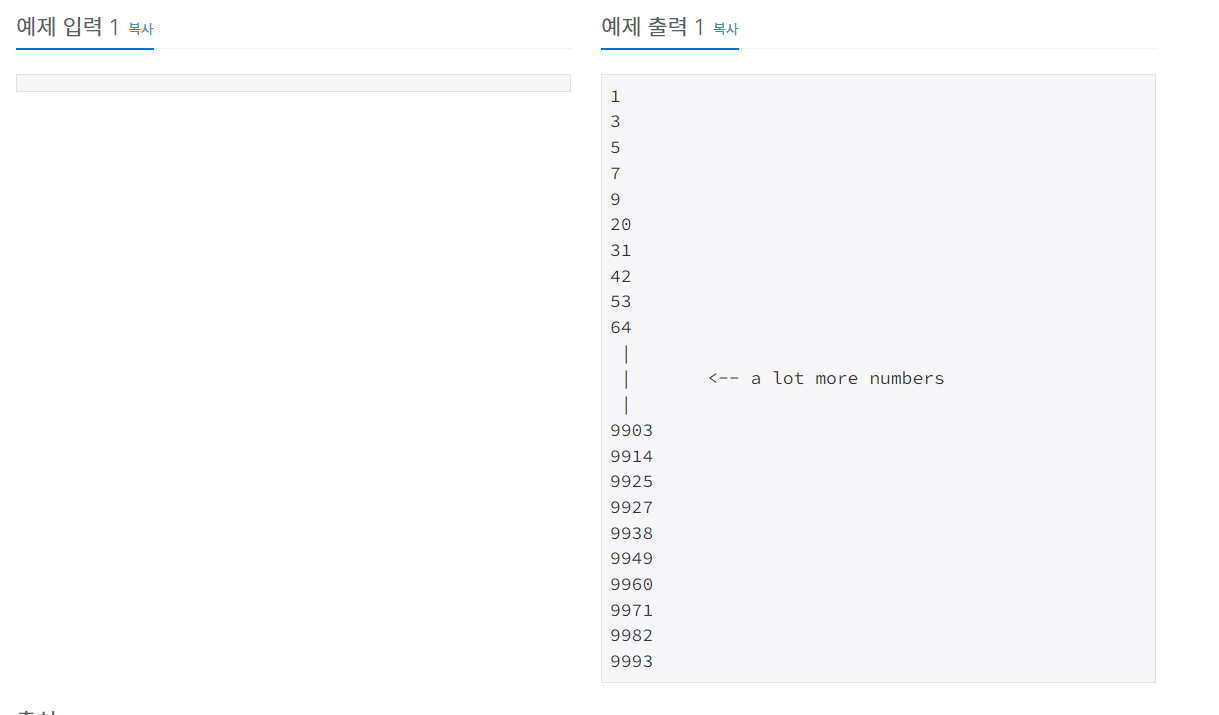
10,000보다 작거나 같은 셀프 넘버를 한 줄에 하나씩 증가하는 순서로 출력한다.

풀이

---

10001 크기에 해당하는 배열과 각 자리수를 더하는 함수를 만든 뒤, 본인과 자리수를 더한 값이
10000보다 작은 경우에 한 해 셀프 넘버로 정의되어 해당 배열의 인덱스 값을 1로 만든다.

셀프 넘버에 해당하는 값을 제외한 배열의 인덱스를 출력한다.

코드

---

#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>

using namespace std;

int arr[10001] = {0,};

int self_num(int n)
{

	int num = n;
	while(n != 0)
	{
		num = num + (n % 10);
		n = n / 10;
	}
	return num;
}

int main()
{		
	cin.tie(NULL);
    ios::sync_with_stdio(false);
	int n;
	for (int i = 1; i <= 10000;i++)
	{
		n = self_num(i);
		if (n <= 10000)
			arr[n] = 1;
	}
	for (int i = 1; i <= 10000;i++)
	{
		if (arr[i] == 0)
		{
			cout << i << endl;
		}
	}
	return 0;
}

각오

---

백준을 오랜만에 풀기 시작했고 그 전에도 잘 풀기는 커녕 파이썬 혼자 독학할 때 조금 한 것 이외에는 거의 들어가지도 않았다.

그러니 당연하게도 실버 5에 해당하는 이 문제에 이해와 풀이도 고군분투하고 있다.
아마 이제 특별한 경우를 제외하고는 문제 풀이에 대한 글에 이런 얘기들을 적지 않을 것이다.

따라서 이 문제는 현재 내 상태를 확인하고 기록하기 위한 것으로
아직 한참 먼 내 코딩 실력을 새기기 위함이다.

꾸준히, 열심히 나아가보자