문제
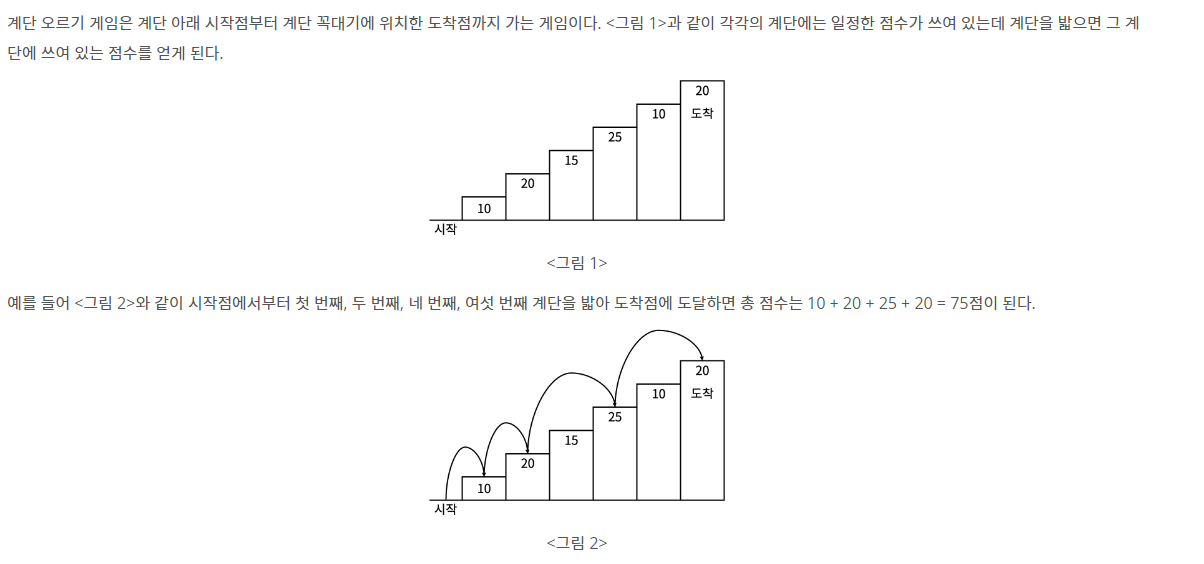
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
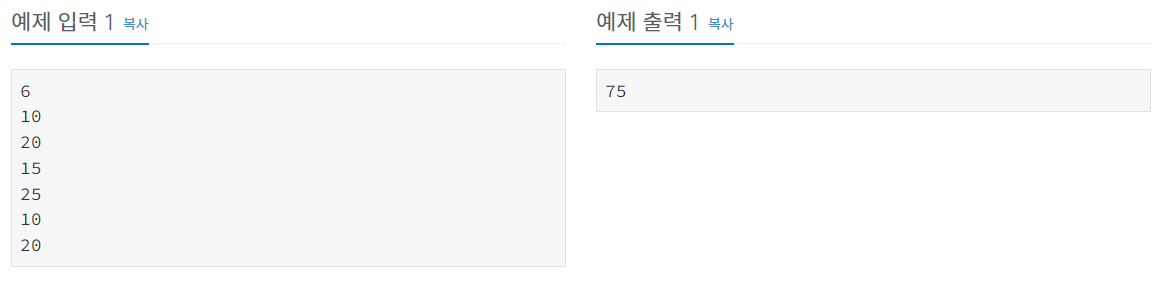
풀이
문제의 조건은 계단은 한 계단 혹은 두 계단씩 올라갈수 있지만 3개의 계단을 올라가서는 안되고 마지막 계단을 반드시 밟아서 도착해야한다.
또한 계단의 점수를 입력받고 이를 각 계단에 대한 최대 점수를 저장할 배열 step 과 arr이 필요하다.
그렇다면 이제 첫번째 계단부터 생각해보자.
첫번째 계단은 첫번째 계단만을 통해 올라갈 수 있다. arr[1] = step[1]
두번째 계단은 첫번째 계단과 두번째 계단을 이어서 올라오거나 바로 두번째 계단으로 올라오는 경우가 있으나 항상 첫번째와 두번째를 이어서 가는 게 최대의 점수를 받는다. arr[2] = step[1] + step[2]
세번째 계단은 첫번째 계단과 세번째 계단으로 가는 방법과 바로 두번째로 계단으로 가고 세번째 계단으로 가능 방법인데 이는 첫번째와 두번째 계단의 점수에 따라 달라질 수 있기 때문에
이를 비교하여 구한다. arr[3] = step[3] + max(arr[1], arr[2])
이제 4번째 계단을 생각해보면 경우의 수가 조금 더 많아졌다.
간단히 생각해보면 계단은 한 개 혹은 두 개로 넘어갈 수 있기 때문에
세번째 계단까지 최대로 오는 경우와 두번째 계단까지 최대로 오는 경우를 비교하면 될 것 같지만
계단 3개를 연속으로 오르는 것은 허용되지 않기 때문에 두번째 계단에서 네번째 계단으로 오는 경우는 이미 계단 두 개를 넘어오는 것이므로 연속이 아니지만 세번째 계단에서 오는 경우 바로 두번째 계단에서 세번째 계단으로 경우가 최대라면 3개 연속이 되버리기 때문에 문제의 조건을 만족시키지 못한다.
그러나 확실히 네번째 계단으로 가는 방법은 크게 세번째 계단 혹은 두번째 계단을 거치는 2개의 방법이고 이후 5번째, 6번째, 7번째도 마찬가지로 하나 이전 계단 혹은 두개 이전 계단을 거치는 방법이다.
그래서 연속을 피하기 위한 조건이 필요한데 하나 이전 계단에서 오는 경우는 반드시 하나 이전의 계단보다 두 개 이전 계단에서 온 경우만 고려하는 것이다.
네번째 계단을 예로 들면 아까 문제가 되었던 세번째 계단에서 오는 경우를 첫번째 계단에서 세번째 계단으로 오는 경우만으로 제한하는 것이다. step[3] + arr[1]
그러면 네번째 계단은 arr[4] = step[4] + max(step[3] + arr[1], arr[2]) 으로 구할 수 있다.
이를 n번째 계단으로 나타나면
n = 4 부터 arr[n] = step[n] + max(step[n-1] + arr[n-3], arr[n-2]) 로 나타낼 수 있다.
이를 점화식으로 사용해 Dynamic Programming 으로 구현하면 문제를 해결할 수 있다.
코드
#include <iostream>
#include <algorithm>
using namespace std;
int step[301];
int arr[301];
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
for(int i = 1; i <= N; i++)
{
int a;
cin >> a;
step[i] = a;
}
arr[1] = step[1];
arr[2] = step[1] + step[2];
arr[3] = step[3] + max(step[1], step[2]);
for(int i = 4; i <= N; i++)
{
arr[i] = step[i] + max(step[i - 1] + arr[i - 3], arr[i - 2]);
}
cout << arr[N];
return 0;
}
느낀점
이 문제가 Dynamic Programming 으로 해결해야겠다는 것은 알았지만 점화식을 어떻게 세우고
Top-down 방식으로 접근해아할지 Bottom-top 으로 접근해야 할지 재귀로 구해야하는지 배열로 구해야하는 지 생각하고 구현하는 데 오래 걸렸다.
재귀을 통해 구현해보려 했으나 시간 초과가 나왔고 결국 배열을 이용한 Bottom-top 방식을
이용했다.
풀이를 좀 찾아보니 메모이제이션 방법으로 재귀함수를 이용해 시간 초과가 발생하지 않게
사용한다고 하는데 코드를 보아도 어떻게 동작하는지 감이 잘 오지 않는다.
Dynamic Programming 풀이를 조금 더 찾아보고 정리하여 익숙해지고 나아가보자!
시간초과로 실패한 코드다...
#include <iostream>
#include <algorithm>
using namespace std;
int step[301];
int arr[301] = {0,};
int step_climb(int n, int con)
{
if (n < 0)
return 0;
if (n == 0)
return step[0];
if (con == 1)
{
return arr[n] = step[n] + step_climb(n - 2, 0);
}
else
return arr[n] = step[n] + max(step_climb(n - 1, 1), step_climb(n - 2, 0));
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
for(int i = 0; i < N; i++)
{
int a;
cin >> a;
step[i] = a;
}
cout << step_climb(N - 1, 0);
return 0;
}