문제

---

크기가 N인 수열 A = A1, A2, ..., AN이 있다. 수열의 각 원소 Ai에 대해서 오큰수 NGE(i)를 구하려고 한다. Ai의 오큰수는 오른쪽에 있으면서 Ai보다 큰 수 중에서 가장 왼쪽에 있는 수를 의미한다. 그러한 수가 없는 경우에 오큰수는 -1이다.

예를 들어, A = [3, 5, 2, 7]인 경우 NGE(1) = 5, NGE(2) = 7, NGE(3) = 7, NGE(4) = -1이다. A = [9, 5, 4, 8]인 경우에는 NGE(1) = -1, NGE(2) = 8, NGE(3) = 8, NGE(4) = -1이다.

입력

---

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다.

출력

---

총 N개의 수 NGE(1), NGE(2), ..., NGE(N)을 공백으로 구분해 출력한다.

풀이

---

주어진 수열의 각 원소에 대해 자신의 오른쪽에서 가장 처음으로 나오는 큰 값을 구하는 것으로

만약 원소 하나하나에 대해 오른쪽으로 하나씩 확인하면서 찾게 될 경우 O($N^2$) 로
시간 초과가 된다.

따라서 위의 방법이 아닌 다른 방법으로 접근헤야 한다.

스택을 이용할 경우 이를 해결할 수 있다.

먼저, 자신의 다음 나오는 원소와 비교한 후 클 경우는 문제 조건에 만족하는
오큰수로 정답이 된다.

그러나 다음 나오는 원소가 자신보다 작을 경우 오큰수를 만족하지 못하므로 해당 원소는
스택에 저장하게 된다.

이후 나오는 원소들에 대해서 우선 스택에 저장된 top 과 비교하여 클 경우
오큰수를 만족하게 되고 아닐 경우 해당 원소를 스택에 저장하게 된다.

top 보다 큰 값을 만나게 된 경우에는 스택에 들어있는 값 중 가장 큰 값이
top 에 저장되어 있는 것으로 나머지 스택의 값에 대한 오큰수도 만난 큰 값이 된다.

아래 그림은 위의 과정을 나타낸 것이다.

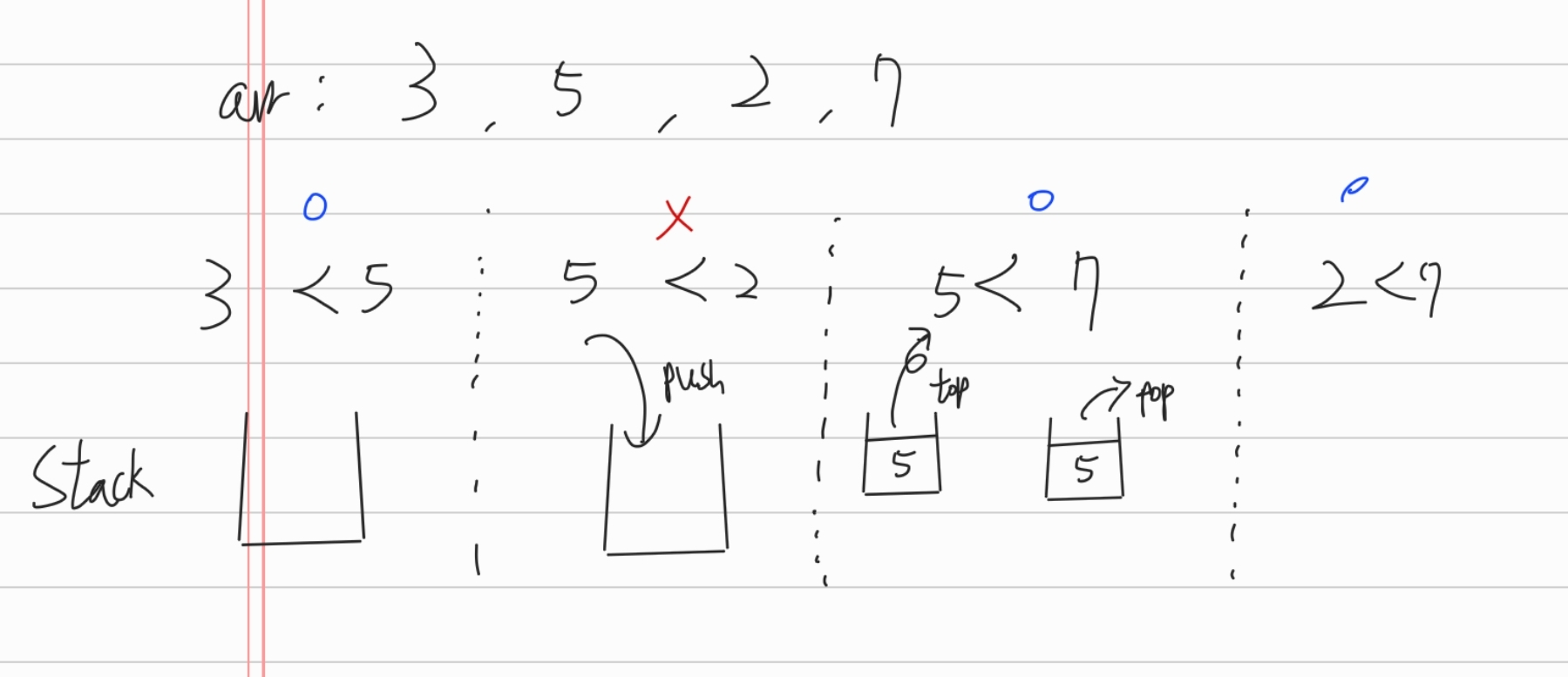
이러한 과정을 통해 주어진 N 개의 원소들이 모두 push 하고 pop 되는 과정이 일어나므로
O($N$) 을 만족해 시간초과 문제를 해결할 수 있다.

코드

---

#include <iostream>
#include <stack>


using namespace std;

int main()
{

    int N;
    cin >> N;

    int arr[1000001];
    int answer[1000001];
    stack<int> my_s;

    for (int i = 0; i < N; i++)
    {
        cin >> arr[i];
    }

    for (int i = 0; i < N; i++)
    {
        while (!my_s.empty() && arr[my_s.top()] < arr[i])
        {
            answer[my_s.top()] = arr[i];
            my_s.pop();
        }
        my_s.push(i);
    }

    while (!my_s.empty())
    {
        answer[my_s.top()] = -1;
        my_s.pop();
    }

    for (int i = 0; i < N; i++)
        cout << answer[i] << " ";
    return 0;
}

리뷰

스택을 이용해야겠다!!
라고 생각하고 구현해보니 결국 2개의 스택을 이용해 O($N^2$) 가 되어버렸다...

시간 복잡도에 대한 개념이 조금씩 잡혀서 안되겠다라는 것을 알게 되었지만

어떻게 구현해야할지 감을 잡는게 아직은 어려운 듯 하다.

구현을 바로 하기 전에 생각해낸 아이디어의 시간 복잡도와 자료형의 범위 등을 먼저
고려하고 푸는 습관을 들이자!!!!