
구종만님의 "프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략"을 기반으로 공부한 내용입니다.📋 목차
1. 도입
2. 와일드카드 (문제 ID: WILDCARD, 난이도: 중)
3. 전통적인 최적화 문제들
4. 합친 LIS (문제 ID: JLIS, 난이도: 하)
5. 원주율 외우기 (문제 ID: PI, 난이도: 하)
6. Quantization (문제 ID: QUANTIZE, 난이도: 중)
7. 경우의 수와 확률
8. 비대칭 타일링 (문제 ID: ASYMTILING, 난이도: 하)
9. 폴리오미노 (문제 ID: POLY, 난이도: 중)
10. 두니발 박사의 탈옥 (문제 ID: NUMB3RS, 난이도: 중)1. 도입
동적 계획법 (Dynamic Programming, DP)
두 번 이상 반복 계산되는 부분 문제들의 답을 미리 저장함으로써 속도의 향상을 꾀하는 알고리즘 설계 기법
- 문제를 나누는 방식에서 분할 정복과의 차이가 존재함
- 문제의 답을 캐시(cache) 라는 메모리 장소에 저장해놓음
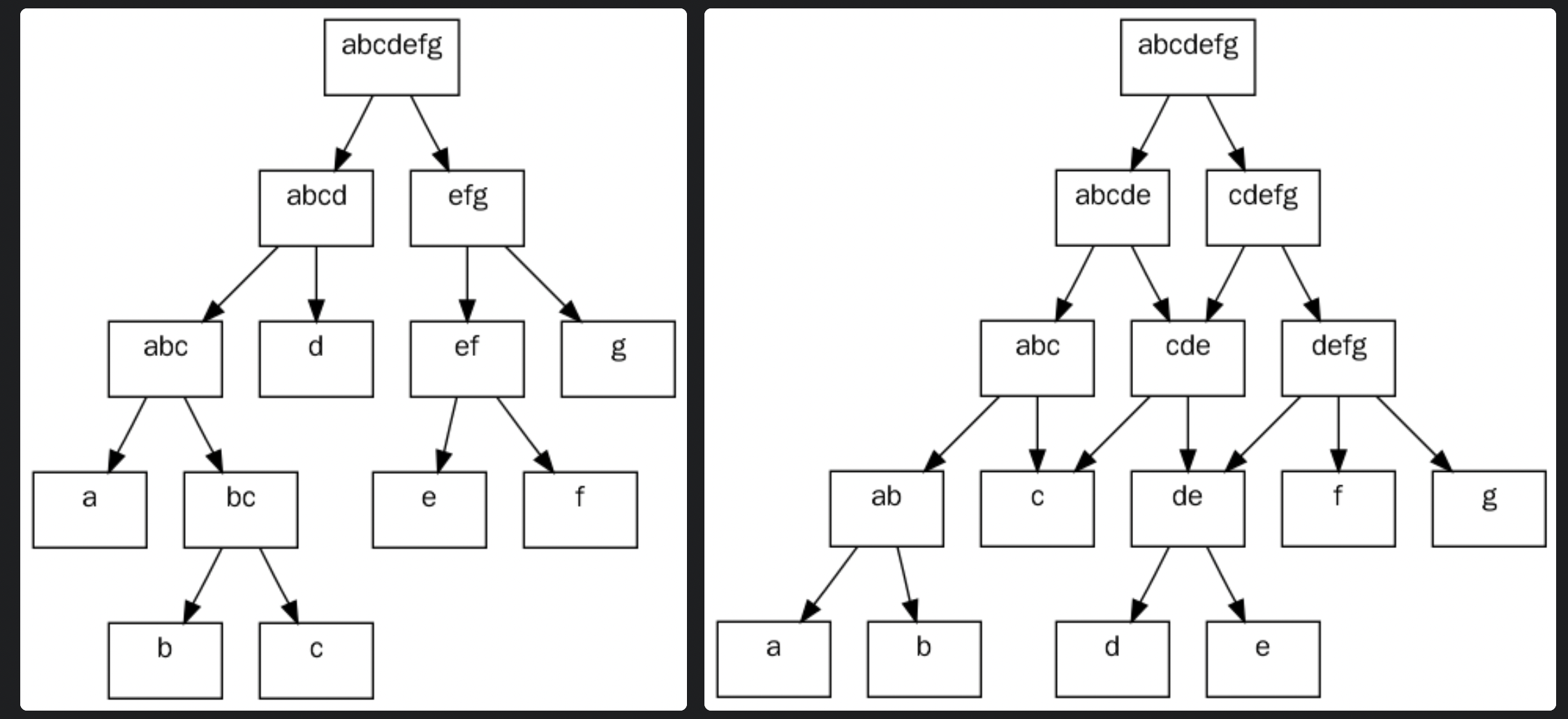
중복되는 부분 문제(Overlapping subproblems)
두 번 이상 계산되는 부분 문제
 |
|---|
재귀 호출을 통해 부분 문제를 해결할 때 중복 계산이 많아지는 단점을 보완하기 위해 동적 게획법이 고안되었다.
▶️ 이항 계수 (binomial coefficient)
이항 계수
n 개의 서로 다른 원소 중에서 r개의 원소를 순서없이 골라내는 방법의 수
아래의 점화식이 성립함
= = ( 단, 0 Kn )
=
= +
=
// 코드 8.1 재귀 호출을 이용한 이항 계수의 계산
int bino(int n, int r) {
// 기저 사례: n = r (모든 원소를 다 고르는 경우) 또는 r = 0 (고를 원소가 없는 경우)
if (r == 0 || n == r) return 1;
return bino(n - 1, r - 1) + bino(n - 1, r);
} |
|---|
점화식을 그대로 적용하면 중복되는 부분 문제가 빈번히 발생한다.
| 🧨 기하급수적으로 증가하는 연산량
 |
|---|
입력인 n과 r이 주어질 때 bino ( n , r ) 의 반환 값이 일정하다는 사실을 이용하면 중복 계산을 제거할 수 있다.
| 📍 방법
- 각 n, r 조합에 대해 답을 저장하는 캐시 배열을 만들어 각 입력에 대한 반환 값을 저장한다.
- 함수는 매번 호출될 때마다 이 배열에 접근해 값이 저장되어 있는지를 확인한 뒤, 저장되어 있다면 이것을 즉시 반환한다.
- 만약 계산되어 있지 않을 경우엔 직접 계산하여 배열에 써넣고 반환한다.
// 코드 8.2 메모이제이션을 이용한 이항 계수의 계산
// -1로 초기화해 둔다.
int cache[30][30];
int bino2(int n, int r) {
// 기저 사례
if (r == 0 || n == r) return 1;
// -1이 아니라면 한 번 계산했던 값이니 곧장 반환
if (cache[n][r] != -1) return cache[n][r];
// 직접 계산한 뒤 배열에 저장
return cache[n][r] = bino2(n - 1, r - 1) + bino2(n - 1, r);
}호출 횟수 비교
 |
|---|
메모이제이션(memoization)
위와 같이 함수의 결과를 저장하는 장소를 마련해 두고, 한 번 계산한 값을 저장해 뒀다가
재활용하는 최적화 기법
▶️ 메모제이션을 적용할 수 있는 경우
프로그래밍에서의 함수는 함수 입력 외에도 전역 변수, 입력 파일, 클래스의 멤버 변수 등 수많은 입력에 의해서 출력이 바뀔 수 있다.
int counter = 0;
int count() {
return counter++;
}위의 함수는 입력을 전혀 받지 않으면서도 매번 다른 결과를 반환한다.
메모이제이션은 참조적 투명 함수의 경우 에만 적용할 수 있다.
- 입력이 고정되어 있을 때, 그 결과가 항상 같은 함수
▶️ 메모제이션 구현 패턴
// a와 b는 각각 [0, 2,500) 구간 안의 정수
// 반환 값은 항상 int형 안에 들어가는 음이 아닌 정수
int someObscureFunction(int a, int b); 위 함수를 한 번 계산하는 데 굉장히 시간이 오래 걸리는 참조적 투명 함수라고 하자.
이를 메모이제이션하여 구현해보자.
// 코드 8.3 메모이제이션의 사용 예
// 전부 -1로 초기화해 둔다
int cache[2500][2500];
// a와 b는 각각 [0, 2500) 구간 안의 정수
// 반환 값은 항상 int형 안에 들어가는 음이 아닌 정수
int someObscureFunction(int a, int b) {
// 기저 사례를 처음에 처리한다
if () return ;
// (a, b)에 대한 답을 구한 적이 있으면 곧장 반환
int& ret = cache[a][b];
if (ret != -1) return ret;
// 여기에서 답을 계산한다
...
return ret;
}
int main() {
// memset()을 이용해 cache 배열을 초기화한다.
memset(cache, -1, sizeof(cache));
}| 📍 고려할 사항
- 항상 기저 사례를 먼저 처리한다.
기저 사례를 먼저 확인하지 않을 경우 cache[] 접근 시 범위를 벗어나는 오류가 발생할 수 있다.
- 함수의 반환 값이 항상 0 이상이므로, cache[]를 모두 -1로 초기화 한다.
-1 일 경우 이 값은 계산된 반환 값이 아닌 것이다.
단, 함수의 반환 값이 음수일 수도 있다면 이 방법은 쓸 수 없다는 것에 주의한다.
- memset()과 같은 초기화 함수를 기억하면 좋다.
단, memset()은 굉장히 제한적인 경우 사용할 수 있다.
▶️ 메모제이션의 시간 복잡도 분석
(존재하는 부분 문제의 수) * (한 부분 문제를 풀 때 필요한 반복문의 수행 횟수)위의 식을 bino2() 에 적용해보면 다음과 같다.
- r의 최대치는 n이므로 bino2( n , r )을 계산할 때 만날 수 있는 부분 문제의 수는 최대 이다.
- 각 부분 문제를 계산할 때 걸리는 시간은 반복문이 없으므로 이다.
- 따라서, bino2( n , r )의 총 시간 복잡도는 이다.
| 🤔 내 아이디어
만약 7*7의 격자라고 가정하면, 원본 격자 값을 2차원 배열에 저장해 놓는다.
첫 값이 격자 7의 크기보다 크다면 바로 NO를 출력한다.
첫 값이 격자 7의 크기보다 작다면 첫 값에 대해 오른쪽으로 가는 경우, 아래쪽으로 가는 경우 2가지로 나눈다.
- 오른쪽으로 가는 경우
- 첫 값 + 도달한 값이 7 이상인 경우 더 이상 실행시키지 않는다.
- 첫 값 + 도달한 값이 7 미만인 경우 오른쪽으로 가는 경우, 아래쪽으로 가는 경우 2가지로 또 나눈다.
- 같은 방향인 오른쪽으로 가는 경우에는 첫 값 + 그 전 값 + 도달한 값이 7 이상인 경우 더 이상 실행시키지 않는다.
- 첫 값 + 그 전 값 + 도달한 값이 7 미만일 경우 다시 오른쪽으로 가는 경우, 아래쪽으로 가는 경우 2가지로 나눈다.
- 다른 방향인 아래쪽으로 가는 경우에는 그 전 값 + 도달한 값이 7 이상인 경우 더 이상 실행시키지 않는다.
- 그 전 값 + 도달한 값이 7 미만인 경우 다시 오른쪽으로 가는 경우, 아래쪽으로 가는 경우 2가지로 나눈다.
- 아래쪽으로 가는 경우
- 위와 똑같이 실행
값을 이동하는 경로는 cursor [ ][ ] 2차원 배열로 만들어서 [x][y] = '해당 값'을 넣어준다.
그리고, 계속 발생하는 부분 문제는 메모이제이션을 통해 재귀적으로 호출해주면 될 것 같다.
 |
|---|
이제, 내 아이디어와 책의 아이디어를 비교해보자 !
▶️ 재귀 호출에서 시작하기
| 📍 재귀적으로 해결하는 완전 탐색 알고리즘을 만들기
- jump ( y , x )
( y , x ) 에서부터 맨 마지막 칸까지 도달할 수 있는 지 여부를 반환하는 함수
- jump () 함수
한 번 호출될 때마다 현 위치에서 아래쪽으로 갈지, 오른쪽으로 갈지를 선택하는 함수
- jumpSize
게임판의 ( y , x ) 위치에 있는 수
- jump ( y + jumpsize , x )
아래쪽으로 갈 경우 마지막 칸에 도달할 수 있는지를 표현하는 함수
- jump ( y, x + jumpsize )
오른쪽로 갈 경우 마지막 칸에 도달할 수 있는지를 표현하는 함수
위의 함수를 합쳐서 재귀적으로 표현하면 아래와 같다.
- jump( y , x ) = jump ( y + jumpsize , x ) || jump ( y, x + jumpsize )
// 코드 8.4 외발 뛰기 문제를 해결하는 재귀 호출 알고리즘
int n, board[100][100];
bool jump(int y, int x) {
// 기저 사례: 게임판 밖을 벗어난 경우
if (y >= n || x >= n) return false;
// 기저 사례: 마지막 칸에 도착한 경우
if (y == n - 1 && x == n - 1) return true;
int jumpSize = board[y][x];
return jump(y + jumpSize, x) || jump(y, x + jumpSize);
}▶️ 메모제이션 적용하기
jump( )는 참조적 투명 함수이므로 메모이제이션으로 중복된 연산을 없앨 수 있다.
// 코드 8.5 외발 뛰기 문제를 해결하는 동적 계획법 알고리즘
int n, board[100][100];
int cache[100][100];
int jump2(int y, int x) {
// 기저 사례
if (y >= n || x >= n) return 0;
if (y == n - 1 && x == n - 1) return 1;
// 메모이제이션
int& ret = cache[y][x];
if (ret != -1) return ret;
int jumpSize = board[y][x];
return ret = (jump2(y + jumpSize, x) || jump2(y, x + jumpSize));
}- 전형적인 Bottom up 방식의 dp 해법이다.
- (0,0)에서 일단 기저 사례까지 jump하고, 거슬러 오면서 true, false를 판가름한다.
- 이미 탐색이 끝난 위치에 대해서는 저장된 값을 반환받으면 된다.
▶️ 다른 해법
7부에서 나오는 그래프로 모델링해보면 아주 간단한 도달 가능성 문제가 된다.
▶️ 동적 계획법 레시피
- 주어진 문제를 완전 탐색을 이용해 해결한다.
- 중복된 부분 문제를 한 번만 계산하도록 메모제이션을 적용한다.
2. 와일드카드 (문제 ID: WILDCARD, 난이도: 중)
| 🤔 내 아이디어
아마 ?문제는 조합을 이용하는 문제가 아닐까라는 생각이 든다.
▶️ * 가 문제로다
-
분할 방법
주어진 패턴이 m개의*를 포함한다고 하면, 이 패턴을*가 나타날 때마다 쪼개자.
그러면, 이 패턴이 문자열에 대응되는지 확인하는 문제를 m+1조각으로 나눌 수 있다.- 패턴 tl?or?ngs → 부분 문제 {t, l?, o, r?ng, s}
아래의의 코드처럼 현재 위치를 가리키는 커서를 옮길 수도 있다.
// 와일드카드 패턴 w가 문자열 s에 대응되는지 여부를 반환한다.
bool match(const string& w, const string& s) {
// w[pos]와 s[pos]를 맞춰나간다.
int pos = 0;
while(pos < s.size() && pos < w.size() &&
(w[pos] == '?' || w[pos] == s[pos]))
++pos;
..
}종료하는 경우의 수를 좀 더 자세히 보자.
(1) s[pos]와 w[pos]가 대응되지 않는다.
- 대응 실패이다.
(2) w 끝에 도달했다.
- 패턴에 *이 하나도 없는 경우.
- 패턴과 문자열의 길이가 정확히 같아야만 패턴과 문자열이 대응된다.
(3) s 끝에 도달했다.
- 패턴은 남았지만 문자열이 이미 끝난 경우.
- 대응 실패 또는 남은 패턴이 전부 *로 구성되어 있다.
- (4)를 호출할 때, 자동으로 걸러진다.
(4) w[pos]가 *인 경우
- *가 몇 글자에 대응될지 모르기 때문에, 0글자부터 남은 문자열의 길이까지를 순회하며 모든 가능성을 검사한다.
- w의 pos+1이후를 패턴 W로 하고, s의 pos+skip 이후를 문자열 s로 해서 match(w
,s)로 재귀 호출했을 때 답이 하나라도 참이면 답은 참이다.
// 코드 8.6 와일드카드 문제를 해결하는 완전 탐색 알고리즘
// 와일드카드 패턴 w가 문자열 s에 대응되는지 여부를 반환한다.
bool match(const string& w, const string& s) {
// w[pos]와 s[pos]를 맞춰나간다.
int pos = 0;
while (pos < s.size() && pos < w.size() && (w[pos] == '?' || w[pos] == s[pos]))
++pos;
// 더 이상 대응할 수 없으면 왜 while문이 끝났는지 확인한다.
// 2. 패턴 끝에 도달해서 끝난 경우: 문자열도 끝났어야 한다.
if (pos == w.size())
return pos == s.size();
// 4. *를 만나서 끝난 경우: *에 몇 글자를 대응해야 할지 재귀 호출하면서 확인한다.
if (w[pos] == '*')
for (int skip = 0; pos + skip <= s.size(); ++skip)
if (match(w.substr(pos + 1), s.substr(pos + skip)))
return true;
// 이 외의 경우에는 모두 대응되지 않는다.
return false;
}중복되는 부분 문제
// 코드 8.7 와일드카드 문제를 해결하는 동적 계획법 알고리즘
// -1은 아직 답이 계산되지 않았음을 의미한다.
// 1은 해당 입력들이 서로 대응됨을 의미한다.
// 0은 해당 입력들이 서로 대응되지 않음을 의미한다.
int cache[101][101];
// 패턴과 문자열
string W, S;
// 와일드카드 패턴 W[w..]가 문자열 S[s..]에 대응되는지 여부를 반환한다.
bool matchMemoized(int w, int s) {
// 메모이제이션
int& ret = cache[w][s];
if (ret != -1) return ret;
// W[w]와 S[s]를 맞춰나간다.
while (s < S.size() && w < W.size() && (W[w] == '?' || W[w] == S[s])) {
++w;
++s;
}
// 더 이상 대응할 수 없으면 왜 while문이 끝났는지 확인한다.
// 2. 패턴 끝에 도달해서 끝난 경우: 문자열도 끝났어야 대응됨
if (w == W.size()) return ret = (s == S.size());
// 4. *를 만나서 끝난 경우: *에 몇 글자를 대응해야 할지 재귀 호출하면서 확인한다.
if (W[w] == '*')
for (int skip = 0; skip + s <= S.size(); ++skip)
if (matchMemoized(w + 1, s + skip))
return ret = 1;
// 3. 이 외의 경우에는 모두 대응되지 않는다.
return ret = 0;
}
⏳ 시간 복잡도
부분문제의 수 * 부분 문제 하나 풀 때의 반복 횟수
패턴과 문자열 길이가 모두 n이면, 부분문제의 수는 n^2개가 된다.
다른 분해 방법
- 첫 *을 찾는 while문
// W[w]와 S[s]를 맞춰나간다
while(s < S.size() && w < W.size() && (W[w] == '?' || W[w] == S[s]))) {
++w;
++s;
} if (s < S.size() && w < W.size() && (W[w] == '?' || W[w] == S[s])))
return ret = matchMemozied(w+1, s_1);- *가 몇 글자 대응하는지 탐색하는 for문
// 4. *를 만나서 끝난 경우: *에 몇 글자를 대응해야 할지 재귀 호출하면서 확인한다.
if (W[w] == '*') {
if (matchMemoized(w+1, s) || (s < S.size() && matchMemoized(w,s+1)))
return ret = 1; }3. 전통적 최적화 문제들
단순히 메모제이션을 적용하기보다 좀더 효율적으로 동적 계획법을 구현할 수 있다.
이번엔 이런 성질들이 성립하는 몇 가지 예제에 대해 알아보겠다.
▶️ 삼각형 위의 최대 경로 (문제 ID: TRIANGLEPATH, 난이도: 하)

완전 탐색으로 시작하기
재귀 함수를 만들건데, 함수에다 현재 위치와 지금까지 만난 숫자들의 합을 전달할 것이다.
- pathSum ( y , x , sum )
현재 위치가 (y,x)이고, 지금까지 만난 수의 합이 sum일 때, 이 경로를 맨 아래줄까지 연장해서 얻을 수 있는 최대 합을 반환하는 함수
이때 아래쪽으로 내려갈 때와 오른쪽으로 내려갈 때의 최대 합을 아래의 점화식으로 표현할 수 있다.
- path1 ( y , x , sum ) = max
무식하게 메모이제이션 적용하기
이 문제에서 가능한 경로의 개수는 삼각형의 가로줄이 하나 늘어날 때마다 두 배씩 늘어나므로 n개의 가로줄이 있을 때 가능한 경로의 수는 이 된다.
n의 최대치가 100이라면 비효율적인 계산이 된다.

path1 함수에 메모이제이션을 적용한 코드이다.
// 코드 8.8 삼각형 위의 최대 경로 문제를 푸는 메모이제이션 코드 (1)
(0,0) 부터 시작한다.
// MAX_NUMBER: 한 칸에 들어가는 숫자의 최대치
int n, triangle[100][100];
int cache[100][100][MAX_NUMBER * 100 + 1];
// (y, x) 위치까지 내려오기 전에 만난 숫자들의 합이 sum일 때
// 맨 아래줄까지 내려가면서 얻을 수 있는 최대 경로를 반환한다.
int path1(int y, int x, int sum) {
// 기저 사례: 맨 아래줄까지 도달했을 경우
if (y == n - 1) return sum + triangle[y][x];
// 메모이제이션
int& ret = cache[y][x][sum];
if (ret != -1) return ret;
sum += triangle[y][x];
return ret = max(path1(y + 1, x, sum), path1(y + 1, x + 1, sum));
}하지만, 이 코드에는 문제가 있다.
(1) 배열의 크기가 입력으로 주어지는 숫자의 범위에 좌우되기 때문에 사용해야 하는 메모리가 너무 크다.
(2) path1() 함수가 특정 입력에 대해서는 완전 탐색처럼 동작된다.
아래와 같은 삼각형의 경로는 항상 합이 다르므로, 똑같은 (y,x) 위치까지 내려왔어도 같은 계산을 두 번 할 일이 없다.
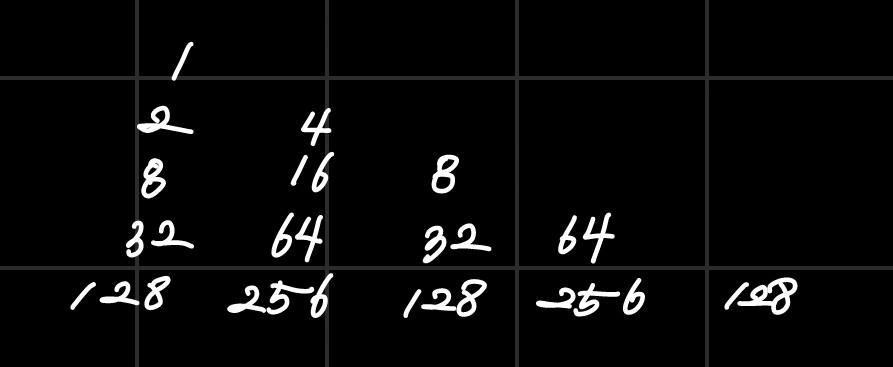
🤔
만약 64라는 숫자에 도달했다면, 64에 오는 삼각형의 경로는 합이 항상 다를 것이고, 같은 게산이 되지 않을 것이다.(이건 모든 삼각형이 다 그런거 아닌가?)
이렇게 규칙을 가지거나 숫자가 다 똑같을 때도 모두 다 더한 값을 재귀호출 해야하니까 비효율적이라는 말인 걸까?
입력 걸러내기
이 알고리즘을 더 빠르게 하기 위해서 재귀 함수의 입력을 두 부류로 나누었다.
(1)
y와 x는 재귀 호출이 풀어야 할 부분 문제를 지정한다.
이 두 입력이 정해지면 앞으로 우리가 만들 수 있는 경로들이 정해진다.
따라서 이것은 앞으로 풀어야 할 조각들에 대한 정보를 주는 입력들이다.
(2)
sum은 지금까지 어떤 걍로로 이 부분 문제에 도달했는지를 나타낸다.
sum은 지금까지 풀었던 조각들에 대한 정보를 주는 입력이다.
이미 결정한 조각인 sum은 앞으로 남은 조각들을 푸는 데 필요하지 않다.
따라서, 재귀함수의 파라미터에 y,x의 정보만 입력으로 받으면 훨씬 알고리즘이 빨라질 것이다.
그리고, 함수의 반환값을 전체 경로의 최대치가 아닌 (y,x) 에서 시작하는 부분 경로의 최대치로 바꾼다.
- path2 ( y , x ) = ( y, x ) 에서 시작해서 맨 아래줄까지 내려가는 부분 경로의 최대 합을 반환하는 항수
- path2 ( y , x ) = triangle [y][x] + max
⏳
전체 시간 복잡도 :
부분 문제의 수는 이고 각 부분문제를 계산하는 데는 상수 시간 밖에 안 걸리므로 전체 시간 복잡도는 똑같이 이다.
// 코드 8.9 삼각형 위의 최대 경로 문제를 푸는 동적 계획법 알고리즘 (2)
int n, triangle[100][100];
int cache2[100][100];
// (y, x) 위치부터 맨 아래줄까지 내려가면서 얻을 수 있는 최대 경로를 반환한다
int path2(int y, int x) {
// 기저 사례
if (y == n - 1) return triangle[y][x];
// 메모이제이션
int& ret = cache2[y][x];
if (ret != -1) return ret;
return ret = max(path2(y + 1, x), path2(y + 1, x + 1)) + triangle[y][x];
}😃
보통 sum을 입력 값으로 넣으면 계산이 복잡해질 거라 감으로 잘 안하는데, 그 이유를 상세하게 알 수 있어서 좋은 예시를 배운 듯함!
최적 부분 구조(Optimal Substructure)
최적 부분 구조
걱 부분 뮨재의 최적 해만 있으면 전체 문제의 최적해를 쉽게 얻어낼 수 있을 경우에 최적 부분 구조가 성립한다고 한다.
많은 문제에서 최적 부분 구조는 굉장히 직관적으로 이해할 수 있어서 증명이 따로 필요하지 않다. 다만, 직관적이지 않은 경우네는 대개 귀류법 혹은 대우를 이용해 증명한다.
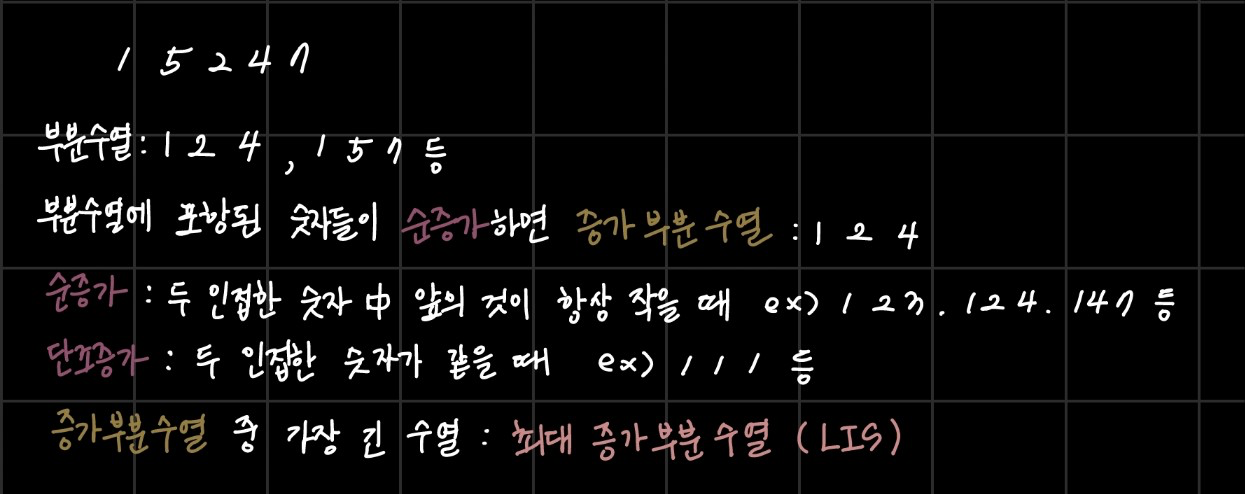
▶️ 최대 증가 부분 수열 (문제 ID: LIS, 난이도: 하)

매우 유명한 동적 계획법 연습 문제이다!
개념은 아래와 같다.
완전 탐색에서 시작하기
먼저, 재귀 함수 lis(A)를 구상해보자.
- lis(A)
lis(A)의 반환 값은 A의 모든 증가 부분 수열을 만든 뒤 그 중 가장 긴 것의 길이이다.
수열의 첫 번째 수를 고르고 나머지 부분을 재귀적으로 만든다.

// 코드 8.10 최대 증가 부분 수열 문제를 해결하는 완전 탐색 알고리즘
int lis(const vector<int>& A) {
// 기저 사례 : A가 비어 있을 때
if (A.empty()) return 0;
int ret = 0;
for (int i = 0; i < A.size(); ++i) {
vector<int> B;
for (int j = i + 1; j < A.size(); ++j)
if (A[i] < A[j])
B.push_back(A[j]);
ret = max(ret, 1 + lis(B));
}
return ret;
}입력 손보기
기존의 정수 배열 입력을 전역으로 빼고, 인덱스 값을 인자로 받게 바꾸었다 (memoziation 적용을 위해)
⏳
시간 복잡도 :
// 코드 8.11 최대 증가 부분 수열 문제를 해결하는 동적 계획법 알고리즘(1)
int n;
int cache[100], S[100];
// S[start]에서 시작하는 증가 부분 수열 중 최대 길이를 반환한다.
int lis2(int start) {
int& ret = cache[start];
if (ret != -1) return ret;
// 항상 S[start]는 있기 때문에 길이는 최하 1
ret = 1;
for (int next = start + 1; next < n; ++next)
if (S[start] < S[next])
ret = max(ret, lis2(next) + 1);
return ret;
}시작 위치 고정하기
lis2()를 호출할 때 어떻게 해야할지에 대한 내용이다.
int maxLen = 0;
for (int begin = 0; begin < n; ++begin)
maxLen = max(maxLen, lis2(begin)); 항상 증가하는 부분 수열 시작 위치를 지적해주어야 하므로, 각 위치를 순회하도록 할 수 있다.
// 코드 8.12 최대 증가 부분 수열 문제를 해결하는 동적 계획법 알고리즘(2)
int n;
int cache[101], S[100];
// S[start]에서 시작하는 증가 부분 수열 중 최대 길이를 반환한다.
int lis3(int start) {
int& ret = cache[start + 1];
if (ret != -1) return ret;
// 항상 S[start]는 있기 때문에 길이는 최하 1
ret = 1;
for (int next = start + 1; next < n; ++next)
if (start == -1 || S[start] < S[next])
ret = max(ret, lis3(next) + 1);
return ret;
}그마저도 귀찮다면 S[-1] 영역을 (논리적으로) 확장시키면 된다.
최종 결과는 list3(-1) - 1이 되어야 한다. (S[-1]은 가상의 영역이므로)
인덱스 값에 유의해서 써야 한다.
더 빠른 해법
O(nlgn)으로 해결하는 알고리즘이다.
최대 길이만 구하면 되므로, 최종적으로 구한 최대 수열의 순서까지는 보장할 필요가 없다.
아래 블로그를 참조하면 더 쉽게 이해할 수 있다.
최적화 문제 동적 계획법 레시피
동적 게획법을 어떤 식으로 생각해야 할지에 대한 대략적인 지침 정도로만 보자.
- 모든 답을 마들어 보고 그 중 최적해의 점수를 반환하는 완전 탐색 알고리즘을 설게하자.
- 전체 답의 점수를 반환하는 것이 아닌, 앞으로 남은 선택들에 해당하는 점수만을 반환하도록 부분 문제 정의를 바꾸자.
- 재귀 호출의 입력에 이전의 선택에 관련된 정보가 있다면 꼭 필요한 것만 남기고 줄이자.
문제에 최적 부분 구조가 성립할 경우에는 이전 선택에 관련된 정보를 완전히 없앨 수도 있다.
여기서 우리의 목표는 가능한 한 중복되는 부분 문제를 많이 만드는 것이다.
입력의 종류가 줄어들면 줄어들 수록 더 많은 부분 문제가 중복되고, 메모이제이션을 최대한도로 활용할 수 있다.
- 입력이 배열이거나 문자열인 경우 가능하다면 적절한 변환을 통해 메모이제이션할 수 있도록 하자.
- 메모이제이션을 적용하자.
🖌️ 삼각형 위의 최대 경로 문제를 대입해보기
-
모든 경로를 만들어 보고 전체 합 중 최대치를 반환하는 완전 탐색 알고리즘 path1() 함수를 만들었다.
-
path1() 함수가 전체 경로의 최대 합을 반환하는 것이 아니라 (y,x) 이후로 만난 숫자들의 최대 합만을 반환하도록 바꿨다.
-
반환 값의 정의를 바꿨기 때문에 이전에 한 선택에 대한 정보인 sum을 입력 받을 필요가 없어졌다. (최적 부분 구조가 성립하므로)
-
이 항목은 필요없었음
-
메모이제이션 적용
4. 합친 LIS (문제 ID: JLIS, 난이도: 하)
입력받은 데이터 중에서 중복 되지 않은 데이터들만 배열로 만들어서 sort하면 될 것 같다.
이 책에서는 A와 B의 배열을 먼저 sort하고 A와 B 배열을 탐색하면서 작은 것들을 순서대로 고르면서 길이를 +1 시켜준다.
(내가 이해한 게 맞는건지 궁금티빟)

// 코드 8.13 합친 LIS 문제를 해결하는 동적 계획법 알고리즘
// 입력이 32비트 부호 있는 정수의 모든 값을 가질 수 있으므로
// 인위적인 최소치는 64비트여야 한다.
const long long NEGINF = numeric_limits<long long>::min();
int n, m, A[100], B[100];
int cache[101][101];
// min(A[indexA], B[indexB]), max(A[indexA], B[indexB])로 시작하는
// 합친 증가 부분 수열의 최대 길이를 반환한다.
// 단 indexA == indexB == -1 혹은 A[indexA] != B[indexB]라고 가정한다.
int jlis(int indexA, int indexB) {
// 메모이제이션
int& ret = cache[indexA + 1][indexB + 1];
if (ret != -1) return ret;
// A[indexA], B[indexB]가 이미 존재하므로 2개는 항상 있다.
ret = 2;
long long a = (indexA == -1 ? NEGINF : A[indexA]);
long long b = (indexB == -1 ? NEGINF : B[indexB]);
long long maxElement = max(a, b);
// 다음 원소를 찾는다.
for (int nextA = indexA + 1; nextA < n; ++nextA)
if (maxElement < A[nextA])
ret = max(ret, jlis(nextA, indexB) + 1);
for (int nextB = indexB + 1; nextB < m; ++nextB)
if (maxElement < B[nextB])
ret = max(ret, jlis(indexA, nextB) + 1);
return ret;
}5. 원주율 외우기 (문제 ID: PI, 난이도: 하)
원주율의 일부가 입력으로 주어질 때, 난이도의 합을 최소화하도록 숫자들을 세 자리에서 다섯 자리까지 끊어 읽어 최소의 난이도를 계산해야 하는 문제이다.
3,4,5의 조합으로 싹 다 끊어보면 되지 않을까? 싶었는데 시간 제한이 1초여서 안될 것 같군..!
일만 자리나 외우라고?
길이 7인 수열인 1111222 에서 쪼갤 수 있는 방법은 {1111,222} 또는 {111,1222}이다.
이런 수열이 n개가 있으면 쪼갤 수 있는 방법의 수는 개가 된다.
길이가 10000인 수열에는 길이 7인 수열이 1428이 있으므로 총 탐색 수는 이다.
이 문제의 시간 제한은 1초인데, 1초에 10억 번 연산이 가능하므로 의 완전 탐색은 불가능 하다.
메모이제이션의 적용
완전 탐색이라도 적절한 알고리즘을 만들면 메모이제이션으로 이 문제를 해결 수 있다.
전체 문제의 최적 해는 아래 세 가지 중 하나이다.
- 길이 3 인 조각의 난이도 + 3글자 빼고 나머지 수열에 대한 최적해
- 길이 4 인 조각의 난이도 + 3글자 빼고 나머지 수열에 대한 최적해
- 길이 5 인 조각의 난이도 + 3글자 빼고 나머지 수열에 대한 최적해
코드를 구성하는 방법은 아래와 같다.
(1) 첫 글자로만 이루어진 문자열과 같으면 난이도는 : 1
(2) 등차 수열이고 공차가 1 또는 -1 이면 난이도는 : 2
(3) 두 개의 수가 번갈아 등장하면 난이도는 : 4
(4) 공차가 1이 아닌 등차 수열의 난이도는 : 5
(6) 이 외에의 난이도는 : 10
[ 등차수열 검사 ]
지정한 구간의 처음 숫자 (M[0]) 와 두 번째 숫자 (M[1]) 의 차의 절대값이 1이고, 세 번째 부터 쭉 반복문을 돌렸을 때 (M[i+1] - M[i]) 의 차가 M[1] - M[0] 와 같으면 (2)를 만족하는 등차수열이다. 당연히 절대값이 1이 아니라면 (4)를 만족할 것 이다.
[ 기저 사례 ]
기저 사례는 수열의 끝에 도달했을 경우일 것이다.
[ 메모이제이션 ]
다시 언급하면, 메모이제이션이란 함수의 결과를 배열에 저정한 후, 한 번 계산한 값을 재활용하는 최적화 기법이다. 여기선 10000 자리 이하의 자연수를 계산하므로 cache[]의 길이를 10002로 두었고, 각 부분문제에서 3,4,5 인 조각의 최적해를 저장하는 곳이다.
// 코드 8.14 원주율 외우기 문제를 해결하는 동적 계획법 알고리즘
const int INF = 987654321;
string N;
// N[a..b] 구간의 난이도를 반환한다.
int classify(int a, int b) {
// 숫자 조각을 가져온다.
string M = N.substr(a, b - a + 1);
// 첫 글자만으로 이루어진 문자열과 같으면 난이도는 1
if (M == string(M.size(), M[0])) return 1;
// 등차수열인지 검사한다.
bool progressive = true;
for (int i = 0; i < M.size() - 1; ++i)
if (M[i + 1] - M[i] != M[1] - M[0])
progressive = false;
// 등차수열이고 공차가 1 혹은 -1이면 난이도는 2
if (progressive && abs(M[1] - M[0]) == 1)
return 2;
// 두 수가 번갈아 등장하는지 확인한다.
bool alternating = true;
for (int i = 0; i < M.size(); ++i)
if (M[i] != M[i % 2])
alternating = false;
if (alternating) return 4; // 두 수가 번갈아 등장하면 난이도는 4
if (progressive) return 5; // 공차가 1 아닌 등차수열의 난이도는 5
return 10; // 이 외는 모두 난이도 10
}
int cache[10002];
// 수열 N[begin..]를 외우는 방법 중 난이도의 최소 합을 출력한다.
int memorize(int begin) {
// 기저 사례: 수열의 끝에 도달했을 경우
if (begin == N.size()) return 0;
// 메모이제이션
int& ret = cache[begin];
if (ret != -1) return ret;
ret = INF;
for (int L = 3; L <= 5; ++L)
if (begin + L <= N.size())
ret = min(ret, memorize(begin + L) + classify(begin, begin + L - 1));
return ret;
}6. Quantization (문제 ID: QUANTIZE, 난이도: 중)
수열과 S가지의 자연수만을 사용하여, 양자화 했을 때 가능한 한 오차 제곱의 합의 최소치를 구하는 문제이다.
평균을 사용하거나, 중앙값을 사용하거나, 표준편차를 사용하는 그런 표본 관련 문제가 아닐까?
하던 대로는 안 된다
- quantize(A) : A에 속한 수를 양자화해서 얻을 수 있는 최소 오차 제곱의 합
양자화 하려는 숫자가 이전과 겹치면 안된다.
'이전'이라는 다른 상태에 영향을 받으므로 최적 부분 조건이 성립하지 않는다.
quantize는 이전 숫자들이 어떤 숫자로 양자화 했는지도 파악해야 한다. (매개변수도 추가)
- quantize(A, U)
U는 한 번 이상 사용한 숫자들의 집합
U의 크기가 10이어도, 개의 부분 문제가 나온다.
구해야 하는 경우의 수가 방대해진다.
답의 형태 제한하기
우리가 시도할 수 있는 방법이 많을 때, 하나의 좋은 전략은 바로
답이 항상 어떤 구조를 가질 것이라고 예측하고 그것을 강제하는 방법이다.
이 문제에서는 같은 숫자로 양자회되는 숫자들은 항상 인접해 있다! 라는 것을 강제할 수 있다.
그래서, 이런 강제를 걸면 좀 더 쉽게 문제에 접근할 수 있다.
수 정렬 -> 인접한 숫자끼리 묶음으로 적절히 분할 -> 각 묶음을 한 숫자로 표현따라서 이 문제는 수열을 s개의 묶음으로 나누는 문제가 된다.
한 개의 구간에 대한 답 찾기
모든 값의 평균을 사용하면 오차를 최소화할 수 있다.
평균을 반올림한 값을 사용하자.
⏳ 전체 시간 복잡도
부분 문제의 수 에 각 부분 문제의 답을 계산하는 데 드는 시간 을 곱한 가 된다.
구현
// 코드 8.15 Quantization 문제의 구현
const int INF = 987654321;
// A[]: 양자화해야 할 수열, 정렬한 상태
// pSum[]: A[]의 부분합을 저장한다. pSum[i]는 A[0] .. A[i]의 합
// pSqSum[]: A[] 제곱의 부분합을 저장한다. pSqSum[i]는 A[0]^2 .. A[i]^2의 합
int n;
int A[101], pSum[101], pSqSum[101];
// A를 정렬하고 각 부분합을 계산한다
void precalc() {
sort(A, A + n);
pSum[0] = A[0];
pSqSum[0] = A[0] * A[0];
for (int i = 1; i < n; ++i) {
pSum[i] = pSum[i - 1] + A[i];
pSqSum[i] = pSqSum[i - 1] + A[i] * A[i];
}
}
// A[lo] .. A[hi] 구간을 하나의 숫자로 표현할 때 최소 오차 합을 계산한다
int minError(int lo, int hi) {
// 부분합을 이용해 A[lo] .. A[hi]까지의 합을 구한다
int sum = pSum[hi] - (lo == 0 ? 0 : pSum[lo - 1]);
int sqSum = pSqSum[hi] - (lo == 0 ? 0 : pSqSum[lo - 1]);
// 평균을 반올림한 값으로 이 수들을 표현한다
int m = int(0.5 + (double)sum / (hi - lo + 1));
// sum(A[i] - m)^2를 전개한 결과를 부분 합으로 표현
int ret = sqSum - 2 * m * sum + m * m * (hi - lo + 1);
return ret;
}
int cache[101][11];
int quantize(int from, int parts) {
// 기저 사례: 모든 숫자를 다 양자화했을 때
if (from == n) return 0;
// 기저 사례: 숫자는 아직 남았는데 더 묶을 수 없을 때 아주 큰 값을 반환한다
if (parts == 0) return INF;
// 메모이제이션
int& ret = cache[from][parts];
if (ret != -1) return ret;
ret = INF;
// 조각의 길이를 변화시켜 가며 최소치를 찾는다
for (int partSize = 1; from + partSize <= n; ++partSize)
ret = min(ret, minError(from, from + partSize - 1) + quantize(from + partSize, parts - 1));
return ret;
}7. 경우의 수와 확률
동적 게획법은 경우의 수를 세거나 확률을 계산하는 문제에서도 사용된다.
▶️ 오버플로에 유의하기
-
Modulo 연산을 자주 사용한다.
- 보통경우의 수를 세는 문제는 입력의 크기에 대해 답이 지수적으로 증가한다. (아니라면 뭐하러 DP를)
- 많은 경우 32-bit 정수형의 한계를 초과할 수 있다.
▶️ 예제: 타일링 방법의 수 세기 (문제 ID: TILING2, 난이도: 하)
| 🤔 내 아이디어
세로로 놓을 수 있는 막대기의 경우의 수를 세아리면 될 것 같다.
홀수 개면 홀수 수만큼 세로로 놓을 수 있고, 짝수 개면 짝수 수만큼 세로로 놓을 수 있다.
n = 5 이면 크게 3가지 경우로 나눌 수 있다.
-
세로로 1개인 경우
- 다음 시작점 : 첫 시작점 + 2 칸
- 다음 시작점 : 첫 시작점 + 2 칸
-
세로로 3개인 경우 (1,2,3번 시작점이 존재)
-
2번째 시작점 : 첫 시작점 + 1 칸
- 3번째 시작점 : 2번째 시작점 + 1 칸 || 2번째 시작점 + 3칸
-
2번째 시작점 : 첫 시작점 + 3칸
- 3번째 시작점 : 2번째 시작점 + 1칸 || 2번째 시작점 + 3칸
-
탈출 조건
- 3번째 시작점이 5의 범위를 넘었을 경우 더 이상 count 하지 않고 2번째 시작점을 다음 경우로
- 2번째 시작점 이 5의 범위를 넘었을 경우 더 이상 count 하지 않고 break하여 다음 경우로
-
-
세로로 5개인 경우
- 1가지
경우의 수가 5일 때 반복되는 규칙을 점화식으로 만들면 문제를 풀 수 있을 것 같다.
이제, 내 아이디어와 책의 아이디어를 비교해보자 !
| 📍 완전 탐색을 이용한 DP
2*n 사각형을 채우는 방법
맨 왼쪽 세로줄이 어떻게 채워져 있느냐로 나눌 수 있다.
- 한 개의 세로 타일로 덮는다.
- 남는 공간은 2*(n-1) 크기의 사각형
- 남는 공간은 2*(n-1) 크기의 사각형
- 두 개의 가로 타일로 덮는다.
- 남는 공간은 2*(n-2) 크기의 사각형
- 재귀호출을 이용해 남은 공간에 대해 계산한다.
점화식
- = 크기의 사각형을 타일로 덮는 방법을 반환한다.
// 코드 8.16 타일링의 수를 세는 동적 계획법 알고리즘
const int MOD = 1000000007;
int cache[101];
// 2 * width 크기의 사각형을 채우는 비대칭 방법의 수를 MOD로 나눈 나머지를 반환한다
int tiling(int width) {
// 기저 사례: width가 1 이하일 때
if (width <= 1) return 1;
// 메모이제이션
int& ret = cache[width];
if (ret != -1) return ret;
return ret = (tiling(width - 2) + tiling(width - 1)) % MOD;
}| ⏳ 시간 복잡도
이 알고리즘에서 부분 문제 수는 이고, 계산 수행 시간이 이므로 전체 시간 복잡도는 이 된다.
최악으로 쪼갤 수 있는 갯수가 개이고, 쪼갠 것을 합치거나 하는 동작이 아닌 계산만 하면 되므로 수행시간은 상수시간이 된다. 그래서 두 개를 곱하면 전체 시간 복잡도가 나온다.
▶️ 예제 : 삼각형 위의 최대 경로 개수 세기 (문제 ID: TRIPATHCNT, 난이도: 중)
| 🤔 내 아이디어
완전 탐색한 후, 나온 결과에서 가장 큰 숫자의 개수를 세면 될 것 같다.
| 📍 두 개의 다른 동적 계획법 쓰기
- 바탕이 되는 최적화 문제를 푼다
- 각 부분 문제마다 최적해의 개수를 게산하는 동적 계획법 알고리즘을 만든다.
1번은 코드 8.9의 path2로 구할 수 있다.
 |
|---|
path2로 구한 구간별 최대 경로를 알고 있다면 탐욕법으로 최대 경로를 파악할 수 있다.
count(y, x) = (y, x)에서 시작해 맨 아래줄까지 내려가는 최대 경로의 수 점화식
// 코드 8.17 삼각형 위의 최대 경로의 수를 찾는 동적 계획법 알고리즘
int countCache[100][100];
// (y, x)에서 시작해서 맨 아래줄까지 내려가는 경로 중 최대 경로의 수를 반환한다.
int count(int y, int x) {
// 기저 사례: 맨 아래줄에 도달한 경우
if (y == n - 1) return 1;
// 메모이제이션
int& ret = countCache[y][x];
if (ret != -1) return ret;
ret = 0;
if (path2(y + 1, x + 1) >= path2(y + 1, x))
ret += count(y + 1, x + 1);
if (path2(y + 1, x + 1) <= path2(y + 1, x))
ret += count(y + 1, x);
return ret;
}▶️ 예제 : 우물을 기어오르는 달팽이
깊이가 n미터인 우물 맨 밑바닥에서 달팽이가 올라오고 있다.
하루에 2미터 씩 올라올 수 있으나, 비가 내리면 1미터밖에 올라오지 못한다.
앞으로 m일간 각 날짜에 비가 올 확률이 정확히 50%일 때,
m일 안에 달팽이가 우물 끝까지 올라갈 확률은 얼마일까? | 📍 경우의 수로 확률 계산하기
m 일 간 가능한 날씨 조합은 {1, 1, 1, 1, ⋯, 1, 1} 부터 {2, 2, 2, 2, ⋯, 2, 2} 까지 이다.
따라서 위 날씨 조합 중 합이 n 이상인 조합의 수를 확인하여, 전체 조합의 수 으로 나누면 된다.
| 📍 완전 탐색 알고리즘
climb(C')
지금까지 만든 날씨 조합 C'에서 원소의 합이 n 이상인 경우의 수
- C'의 종류가 너무 많으므로 Memoization을 적용할 수 없다.
- 과거에 한 선택에 대한 정보는 최소한도로 줄이는 것이 좋다.
climb(days, climbed)
지금까지 만든 날씨 조합 C' 크기가 days이고 그 원소들의 합이 climbed일 때 C'를 완성해서 원소의 합이 n 이상인 경우의 수
- days만큼 지났을 때 climbed까지 올라왔다면 그 뒤로는 이미 계산된 결과를 사용하면 된다.
// 코드 8.18 우물을 기어오르는 달팽이 문제를 해결하는 동적 계획법 알고리즘
int n, m;
int cache[MAX_N][2 * MAX_N + 1];
// 달팽이가 days일 동안 climbed미터를 기어올라 왔다고 할 때,
// m일 전까지 n미터를 기어올라갈 수 있는 경우의 수
int climb(int days, int climbed) {
// 기저 사례: m일이 모두 지난 경우
if (days == m) return climbed >= n ? 1 : 0;
// 메모이제이션
int& ret = cache[days][climbed];
if (ret != -1) return ret;
return ret = climb(days + 1, climbed + 1) + climb(days + 1, climbed + 2);
}| 🥹 여담
아이디어를 생각하고 이해하는 것 까지는 수월한데 점화식으로 만드는 것, 함수 파라미터로 어떤 걸 넘겨줄 것인지 생각하는 것, 부분 문제를 정의하는 것이 아직은 쉽지 않은 것 같다. 최대한 블로그 적으면서 익숙해져야 하고 필자가 알려준 알고리즘은 어떻게든 머리에 넣어야 한다!
▶️ 예제 : 장마가 찾아왔다 (문제 ID: SNAIL, 난이도: 하)
점화식
+
| 📍 경우의 수 계산하기 레시피
- 모든 답을 직접 만들어서 세어보는 완전 탐색 알고리즘을 설계한다.
- 재귀 호출 각 단계에서 고르는 각 선택지는 다음과 같은 속성이 성립해야 한다.
- 모든 경우는 해당 선택지에 포함된다.
- 어떤 경우도 두 개 이상의 선택지에 포함되지 않는다.
- 최적화 문제를 해결할 때처럼 이전 조각에서 결정한 요소들에 대한 입력을 없애거나 변형해서 줄인다.
- 재귀 함수는 앞으로 남아 있는 조각들을 고르는 경우의 수만을 반환해야 한다.
- Memoization을 적용한다.
8. 비대칭 타일링 (문제 ID: ASYMTILING, 난이도: 하)
위의 타일링 문제에서 좌우대칭인 타일은 제외한 타일링 방법의 수를 계산하는 문제다.
▶️ 완전 탐색의 함정
비대칭 타일링의 수 = 전체 타일링의 수 - 대칭 타일링의 수
-
대칭 타일링 수를 세는 단계
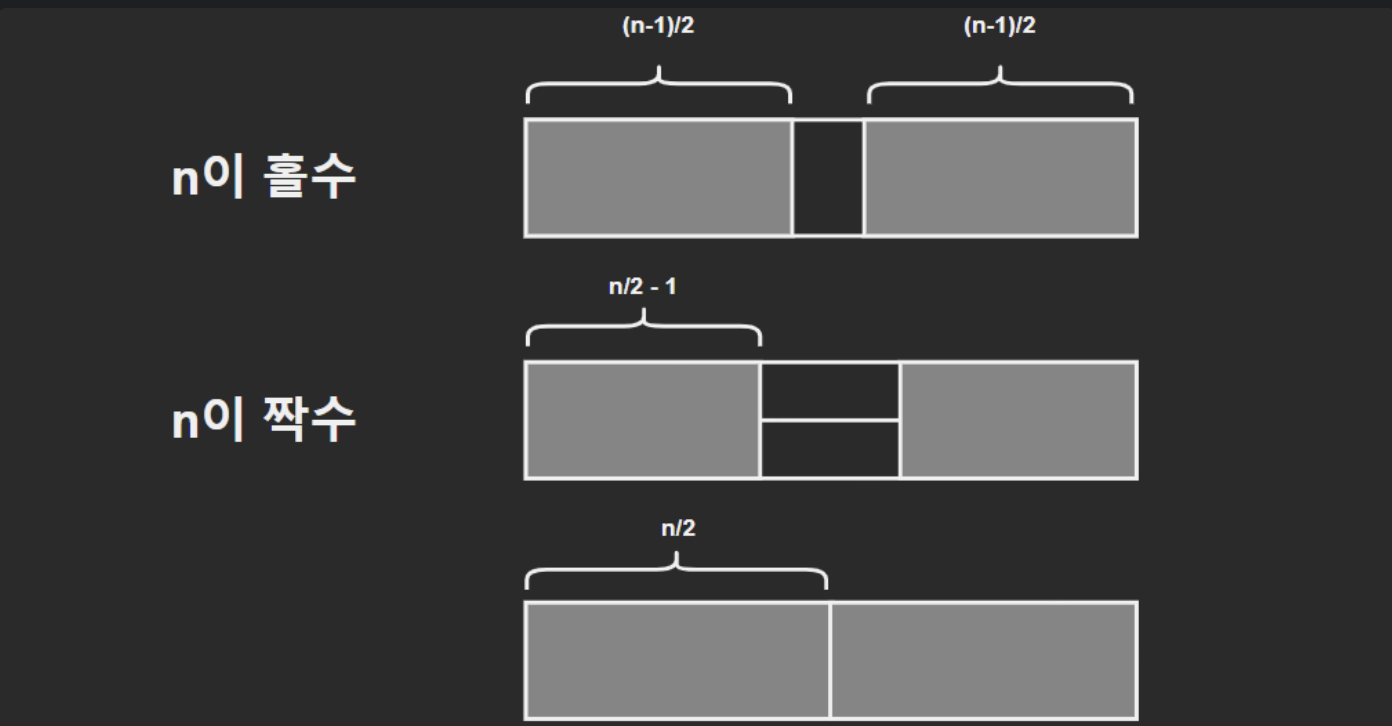
- n이 짝수인 경우와 홀수인 경우를 나눈다.
- n이 홀수, 정가운데 세로운은 세로 타일 하나로 덮여야 한다.
- n이 짝수, 정가운데 세로줄 둘을 가로 타일로 덮거나, 절만을 기준으로 대칭인 경우다.
- 경계를 나누고 한쪽을 채우면, 다른 한쪽은 자연스럽게 결정된다. (대칭이므로)
- n이 짝수인 경우와 홀수인 경우를 나눈다.
-
tiling() 반환 값은 반드시 양수지만 뺄셈의 결과는 음수일 수 있으므로 MOD로 나누기 전에 MOD를 미리 더해준다.
// 8.19 비대칭 타일링 문제를 해결하는 동적 계획법 알고리즘
// 2 * width 크기의 사각형을 채우는 비대칭 방법의 수를 반환한다.
int asymmetric (int width) {
if (width % 2 == 1)
return (tiling(width) - tiling(width / 2) + MOD) % MOD;
int ret = tiling(width);
ret = (ret - tiling(width / 2) + MOD) % MOD;
ret = (ret - tiling(width / 2 - 1) + MOD) % MOD;
return ret;
}▶️ 직접 비대칭 타일링의 수 세기
-
모든 타일링 방법을 만들어 보고 좌우 대칭이 아닌 것만을 걸러낸다.
- 메모제이션 적용이 불가함
- 타일링 방법의 대칭 유무를 판단하기 위해서는 과거에 선택한 조각들에 대한 정보를 전부 재귀 호출에 전달해야 함
- 양쪽 끝에서부터 동시에 만들어 나가는 방법을 사용하자
-
아래 이미지에서 a, b와 c, d인 케이스 두 가지로 분류하면 다음처럼 로직을 작성할 수 있다.
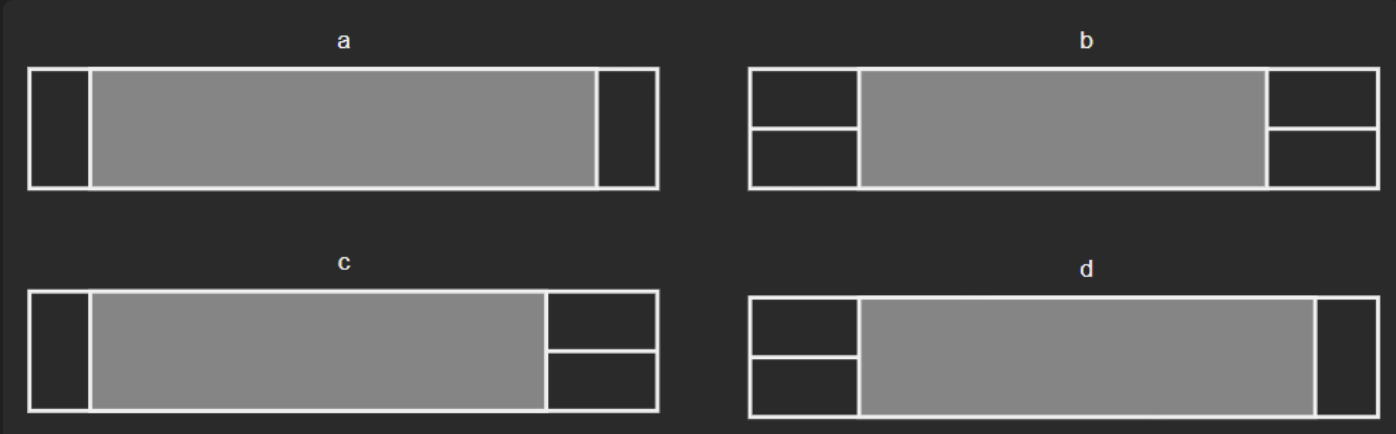
- a, b : 가운데 남은 회색 부분을 탐색하는 방법을 재귀호출로 찾는다. 대칭이 아닌 경우여야 한다.
- c, d : 가운데 남은 회색 부분을 탐색하는 방법을 찾는다. 대칭이어도 상관없다.
// 코드 8.20 직접 비대칭 타일링의 수를 세는 동적 계획법 알고리즘
int cache2[101];
// 2 * width 크기의 사각형을 채우는 비대칭 방법의 수를 반환한다
int asymmetric2(int width) {
// 기저 사례: 너비가 2 이하인 경우
if (width <= 2) return 0;
// 메모이제이션
int& ret = cache2[width];
if (ret != -1) return ret;
ret = asymmetric2(width - 2) % MOD;
ret = (ret + asymmetric2(width - 4)) % MOD;
ret = (ret + tiling(width - 3)) % MOD;
ret = (ret + tiling(width - 3)) % MOD;
return ret;
}| ⏳ 시간 복잡도
asymmetric2의 부분 문제 수인 이 최종 시간 복잡도가 된다.
▶️ 스캐폴딩으로 테스트하기
이 문제는 입력을 생성하기 쉽고, 느리지만 확실히 정답임을 보일 수 있는 알고리즘이 존재한다.
- 모든 타일링 방법을 만들어보고 대칭인지 확인하기
따라서 스캐폴딩을 통해 테스트를 거치면 알고리즘의 정당성을 증명할 수 있다.
9. 폴리오미노 (문제 ID: POLY, 난이도: 중)
8개의 댓글
[와일드카드]
-
이 문제를 이해하지 못하는 이유는 가장 처음에 "가 그래서 왜 문제인 건데?"를 명확히 짚고 넘어가지 않았기 때문도 있다고 생각합니다. 왜 ?는 깊게 고려하지 않으면서, 는 문제라고 하는 걸까요?
-
코드 8.7을 이해하려면 코드 8.6의 문제점을 찾아내야 합니다. 해당 코드로 문제를 풀 수 없기 때문이 아니라, "비효율적으로 동작하는 케이스"가 존재하기 때문입니다. (패턴 *a, 문자열 aaaaaab는 절대로 조합이 불가능하지만 코드 8.6은 *에 대응시키는 수많은 경우의 수를 검사하게 됨) => 이해 안 가면 질문해주세요.
-
코드 8.7은 결국 8.6의 문제점을 개선하고자 메모이제이션을 적용한 방법을 보여주는 겁니다. 해당 로직이 이해가 안 간다면, 제 블로그에 올려둔 공백의 cache 테이블을 직접 채워보면서 동작을 확인해보세요. (확인할 겁니다 ^^)
-
부분문제의 수가 왜 N^2인가요? 최종 시간복잡도는 왜 O(N^3)일까요?
-
다른 분해 방법은 O(N^3)에서 O(N^2)으로 떨어트리기 위해 while문 내부의 반복문을 모두 제거하는 과정입니다. 굳이 반복을 하지 않아도, 메모이제이션과 재귀를 잘 활용하면 반복을 줄일 수 있음을 보여주는 거예요. 말로는 설명이 힘드니 내일..












"ret이 cache[a][b]에 대한 참조형(reference)인 것에 유의한다."
자바로 문제 푸실 거라서 해당되지 않는 내용입니다. 본인에게 필요한 정보만 간추리는 게 좋아요!