[14501번] 퇴사 준비하기 ( DP, 탑 다운인데 뒤에서 부터 접근하는 문제, 백만장자와 유사)

---

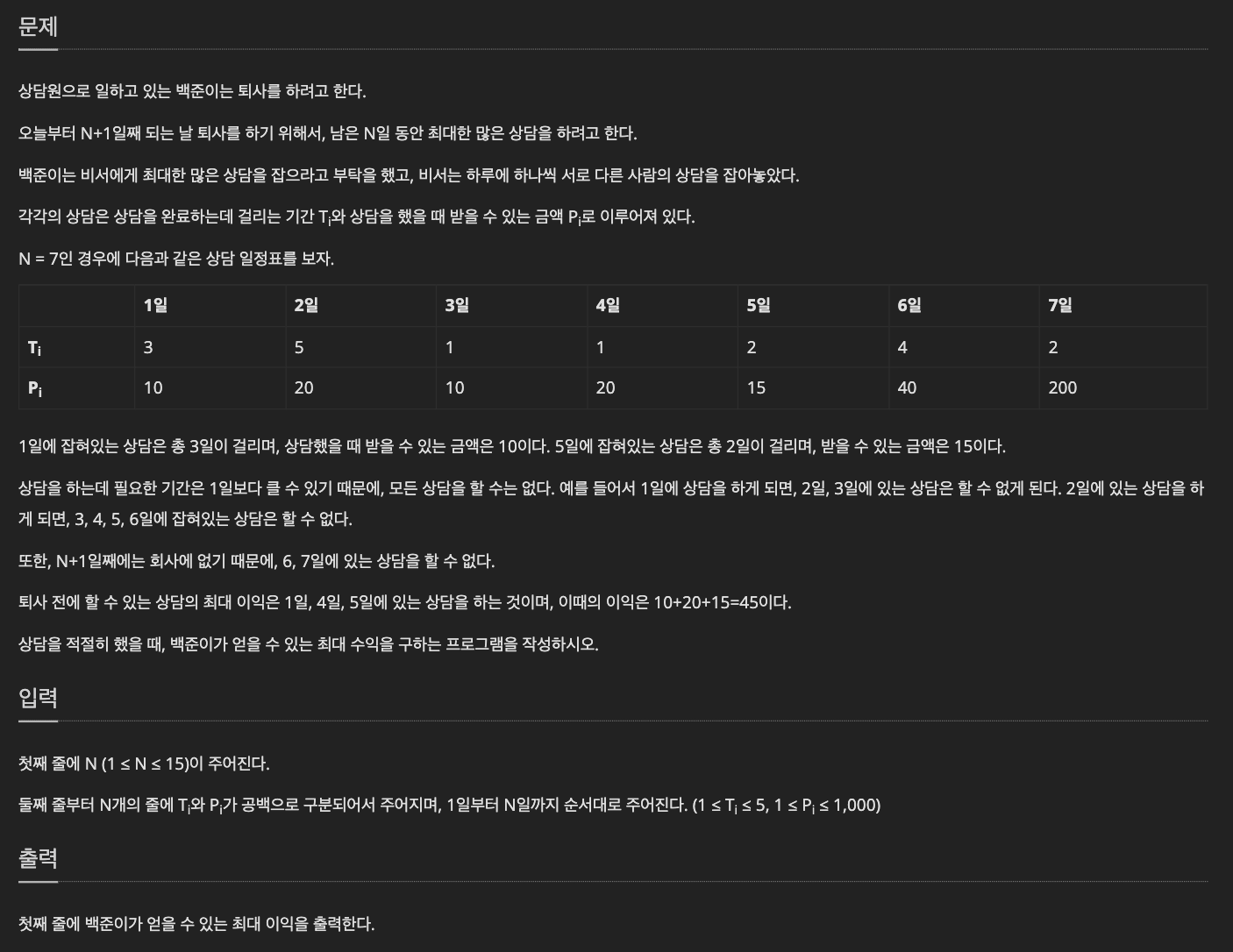
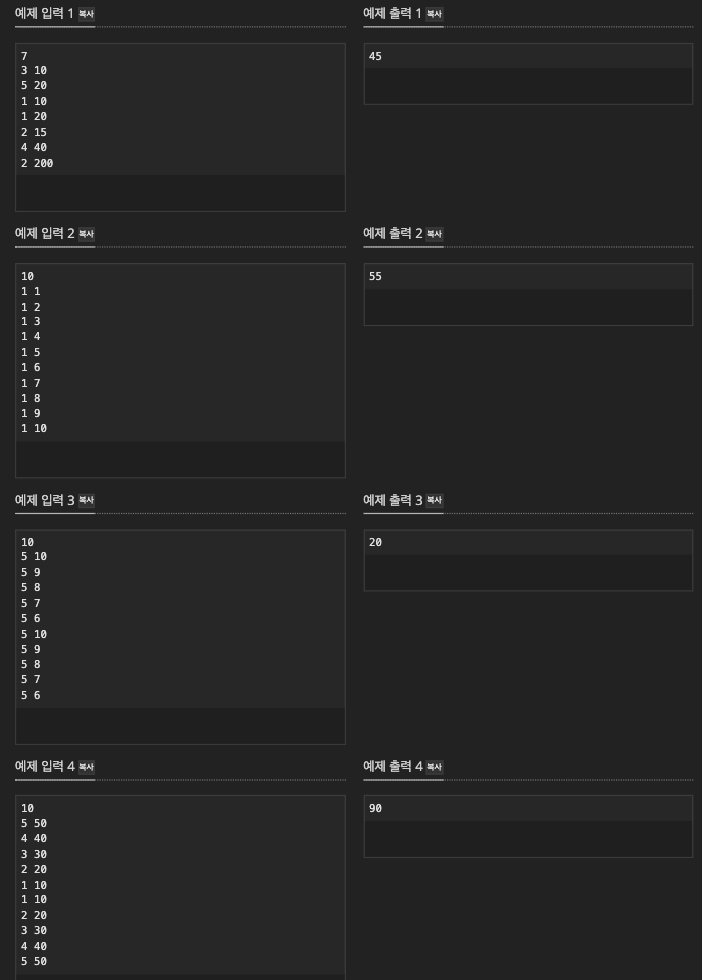
예제가 많다.
탑 다운이랑 뒤에서 부터 접근하는 문제랑 같은 말인가.?!

---

✅ 점화식

dp[i] = i번쨰 날부터 퇴사날까지 벌 수 있는 최대 수입

//오늘 시작되는 상담을 했을 때 퇴사일까지 끝나지 않는 경우
dp[i] = dp[i]+1 
// 오늘 시작되는 상담을 했을 때 퇴사일 안에 끝나는 경우
dp[i] = Math.max(dp[i+1],dp[i+T[i] + P[i]) 

배열을 손으로 써보면 아래와 같다.

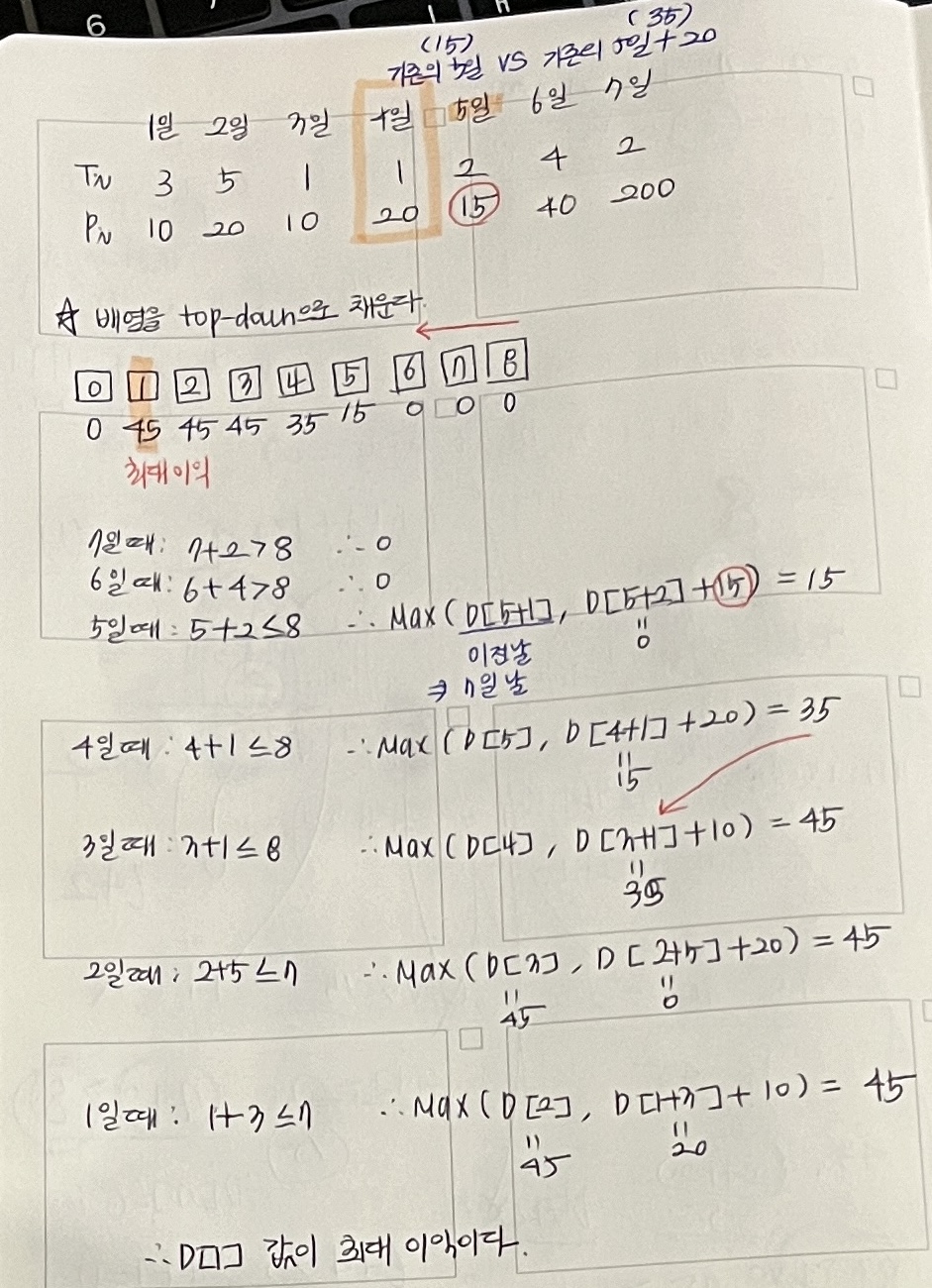
이때까지 풀었던 문제와 다른 점은
배열을 (n + 2) 만큼 넣어줘야 한다는 것
1일째부터 7일째까지에서 바텀업이면 0번쨰 = 0이 된다.
여기서는 뒤에서부터 생각하므로 8번째 = 0이 된다.

---

✅ 코드

위의 이론을 잘 이해하니까 구현하는 데는 10분도 채 안걸린 것 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	static int[] dp;
	static int[] T;
	static int[] P;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		int n = Integer.parseInt(br.readLine());
		dp = new int[n + 2];
		dp[n + 1] = 0;
		T = new int[n + 1];
		P = new int[n + 1];
		for (int i = 1; i < n + 1; i++) {
			st = new StringTokenizer(br.readLine());
			T[i] = Integer.parseInt(st.nextToken());
			P[i] = Integer.parseInt(st.nextToken());
		}

		for (int i = n; i >= 1; i--) {
			if (i + T[i] > n + 1) {
				dp[i] = dp[i + 1];
			} else {
				dp[i] = Math.max(dp[i + 1], dp[i + T[i]] + P[i]);
			}
		}

		System.out.println(dp[1]);

	}
}

---