✅ DP
이 문제는 4를 다 채웠다고 가정하고 5를 구하는 부분 문제로 나눌 수 있다.
dp로 풀 수 있다는 판단이 선다.
그러면, 점화식을 구해야 한다.
점화식 D[ ] (2차원 까지 필요없을 것 같아 1차원으로 생성함) 의 정의를 내려보자.
D [ ] = 2 X N 타일을 채우는 경우의 수
D[N-1], D[N-2], ... D[N-5] 등 모든 부분문제가 채워졌다고 가정하고,
N 바로 직전에 구해야 하는 N-1, N-2 에서 N 의 길이를 만들기 위한 점화식을 세워보자
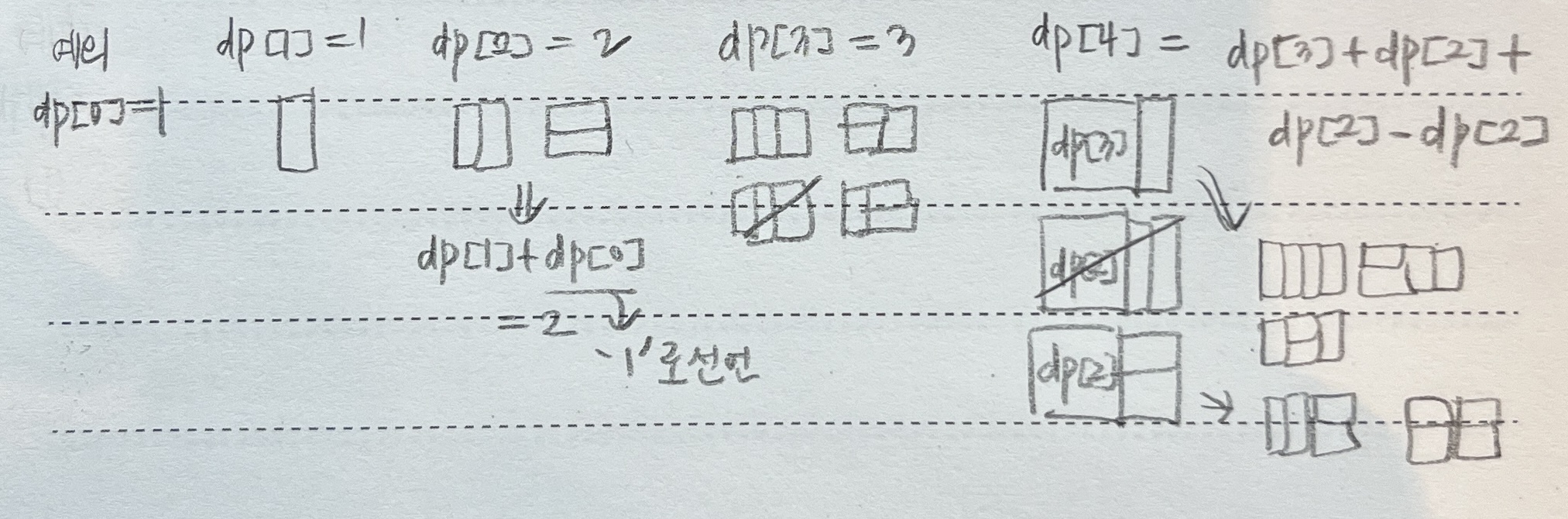
D[N] = D[N-1] + D[N-2] 가 된다.
( 2 * D[N-2]이 아님을 주의하자! )
그림을 그려보면 더 쉽다.

✅ 탑 다운
import java.util.Scanner;
public class Main {
static int D[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
D = new int[n + 1];
//알 수 있는 값을 미리 초기화 시켜 놓자.
D[0] = 1;
D[1] = 1;
//1넣었을 때 D[2]를 초기화 해줘서 인덱스 에러 발생
//D[2] = 2;
tiling(n);
//같은 거
System.out.println(D[n]);
System.out.println(tiling(n));
}
private static int tiling(int n) {
if (D[n] != 0) { // 이 조건을 통해 배열 인덱스 범위가 3부터 시작이 된다.
return D[n];
}
//이렇게 해주면 D[n] 의 정의는 경우의 수에서 10007로 나눠진 나머지의 수가 될 듯.
D[n] = (tiling(n - 1) + tiling(n - 2)) % 10007;
return D[n];
}
}1 을 넣었을 때 D[2]를 초기화주니까 배열 인덱스 에러 발생했다.
고쳐주니까 맞았다.
✅ 바텀 업
바텀 업은 for 문으로 인덱스 2부터 마지막까지 차근차근 넣어주는 과정이 필요하다.
import java.util.Scanner;
public class Main {
static int D[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
D = new int[n + 1];
//알 수 있는 값을 미리 초기화 시켜 놓자.
D[0] = 1;
D[1] = 1;
//1넣었을 때 D[2]를 초기화 해줘서 인덱스 에러 발생
//D[2] = 2;
for (int i = 2; i <= n; i++) {
tiling(i);
}
//같은 거
System.out.println(D[n]);
}
private static int tiling(int n) {
D[n] = (D[n - 1] + D[n - 2]) % 10007;
return D[n];
}
}✅ 시도 2 코드 및 풀이
dp[0] = 1 을 해줘야 한다.
2*2 의 타일을 만드는 경우만 점화식의 예외 상황이 되는데, 선언한 점화식으로는 1 이라는 값이 나오기 때문에 2 라는 값이 나오도록 만들어줘야 하기 때문이다.
import java.util.Scanner;
public class Main {
static int[] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
}
System.out.println(dp[n]);
}
}두 방식 모두 통과!

