⭐️ 변수 위치 -> 실수가 좀 많은 부분 -> 실력 -> 고치자!
일단 바보 같은게 max는 i마다 갱신이 필요하므로 for문 안에 들어가야 했다!!
변수 위치 놓는 거에 신경쓰자..!
for (int i = 1; i < N; i++) {
int max = 0;
for (int j = i - 1; j >= 0; j--) {
if (A[j] > A[i]) {
max = Math.max(dp[j], max);
}
}
dp[i] = max + 1;
}✅ 점화식
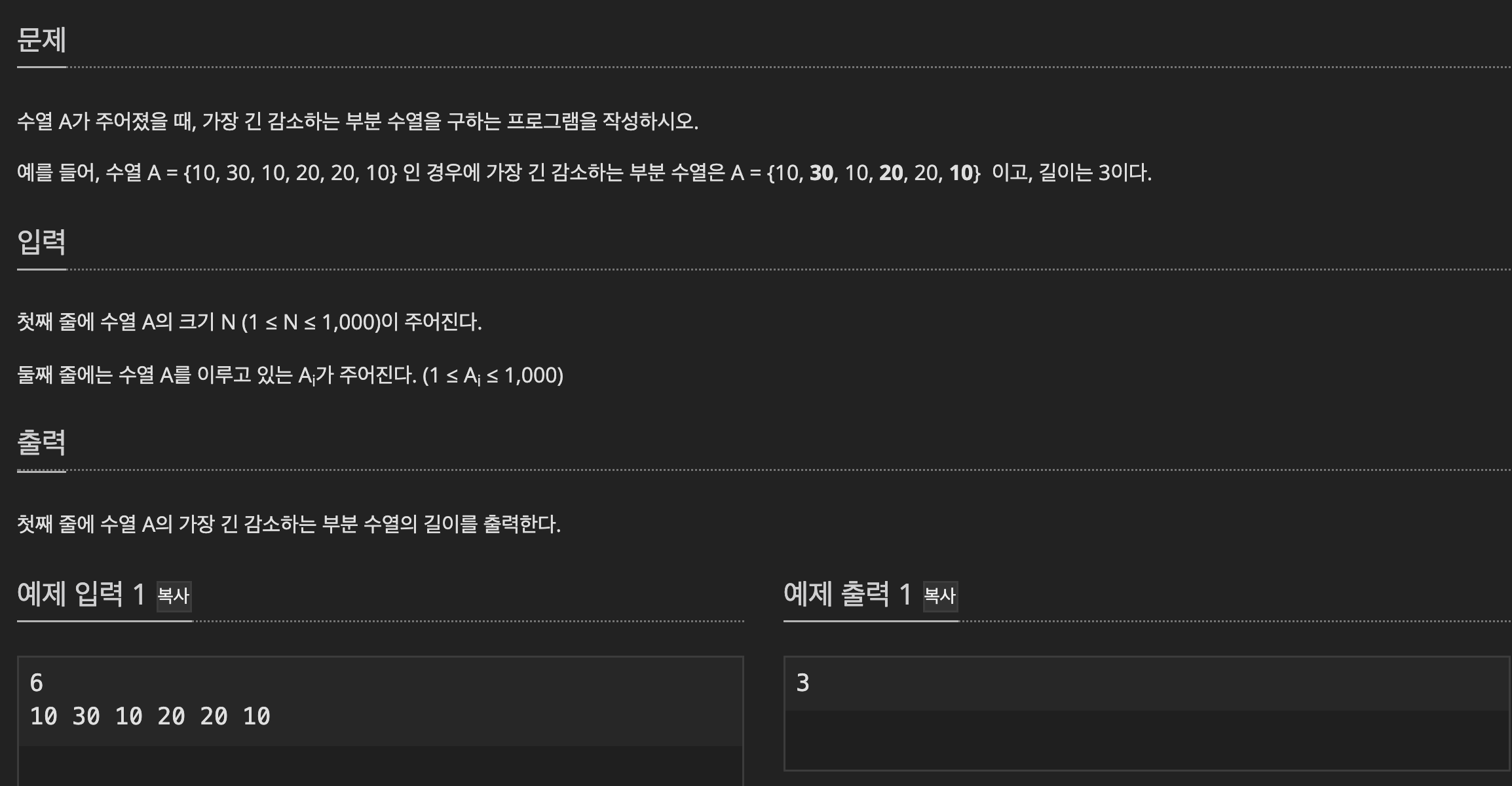
dp[n] = n 번째 일 때 들어갈 수 있는 가장 긴 부분 수열
계산은 0에서 n-1번째 중에서 n번 째보다 큰 수 중에서 가장 길이가 긴 부분 수열 + 1 해주면 된다!
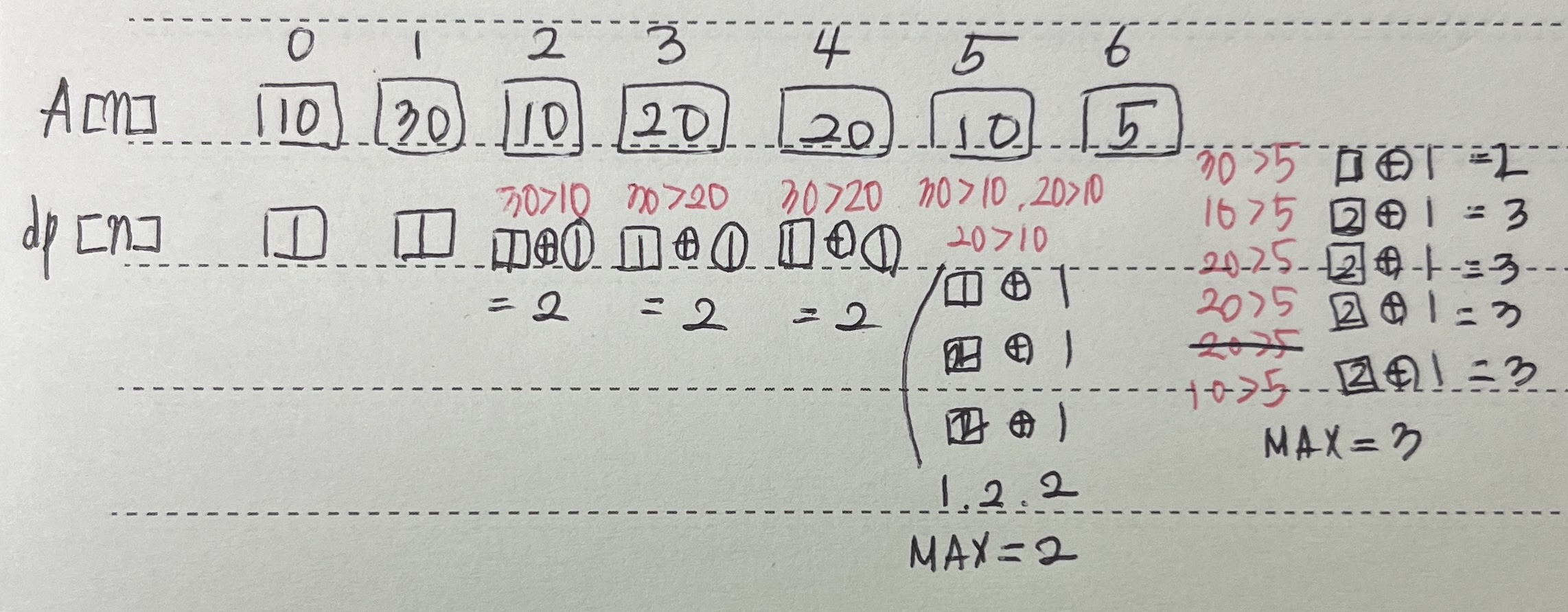
✅ 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int N = 0;
static int[] A;
static int[] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
A = new int[N];
dp = new int[N];
Arrays.fill(dp, 1);
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
A[i] = Integer.parseInt(st.nextToken());
}
for (int i = 1; i < N; i++) {
int max = 0;
for (int j = i - 1; j >= 0; j--) {
if (A[j] > A[i]) {
max = Math.max(dp[j], max);
}
}
dp[i] = max + 1;
}
int max = 0;
for (int i = 0; i < N; i++) {
max = Math.max(dp[i], max);
}
System.out.println(max);
}
}
