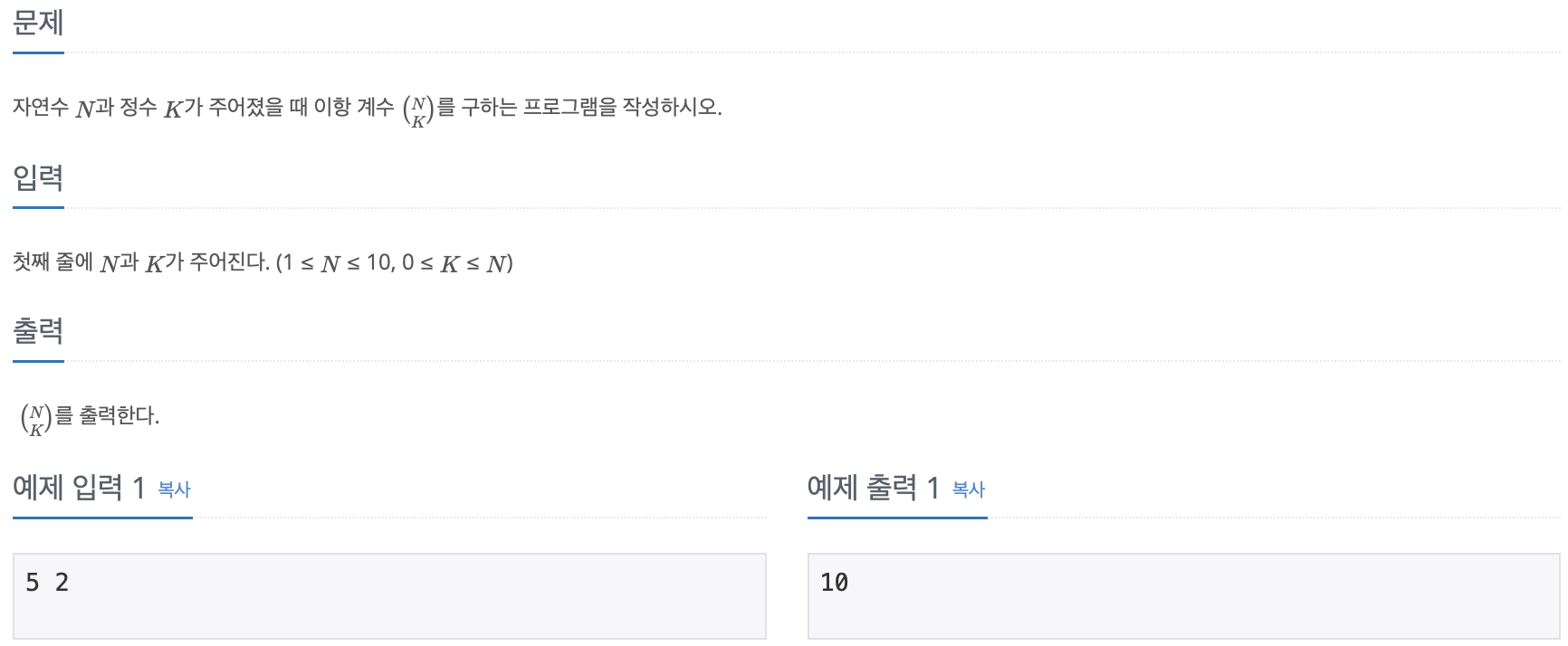
✅ 조합
조합은 점화식을 알면 쉽다.
중복없이 5개 중에 3개를 뽑는다고 가정하면. 5C3 = 4C3 + 4C2 이다.
이를 알고리즘적으로 풀어 나타내면.D[5][3] = D[4][3] + D[4][2]
즉, D[i][j] = D[i-1][j] + D [i-1][j-1] 이 된다.
- 배열 안의 값은 조합의 경우의 수이다!
- i=2 부터 n까지
- j=1부터 i보다 작을 때 까지
- 배열은 [n+1][n+1] 크기
- 5C2 => 0번부터 5번째 행 2번째 열 인덱스!
[ 초기화 세팅 ]
- i 개 중 아무것도 선택안하는 경우는 1개!
- i 개 중 1개 선택하는 경우는 i개!
- i 개 중 i개 선택하는 경우는 1개!그려서 이해해보자.

✅ 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int r = Integer.parseInt(st.nextToken());
int Combination[][] = new int[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
Combination[i][0] = 1; //아무것도 안 뽑는 경우 = 1가지
Combination[i][i] = 1;
Combination[i][1] = i;
}
for (int i = 2; i <= n; i++) {
for (int j = 1; j < i; j++) {
// 고르는 수의 개수가 전체 개수를 넘을 수 없다.
Combination[i][j] =
Combination[i - 1][j] + Combination[i - 1][j - 1];
}
}
System.out.println(Combination[n][r]);
}
}🆙 재도전 코드
import java.io.IOException;
import java.util.Scanner;
public class Main {
static int cache[][];
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
cache = new int[n + 1][k + 1];
int result = Combination(n, k);
System.out.println(result);
}
private static int Combination(int n, int k) {
if (n == k || k == 0) {
return cache[n][k] = 1;
}
if (cache[n][k] != 0) {
return cache[n][k];
}
return cache[n][k] = Combination(n - 1, k - 1) + Combination(n - 1, k);
}
}
