백준 24267 문제<시간복잡도>

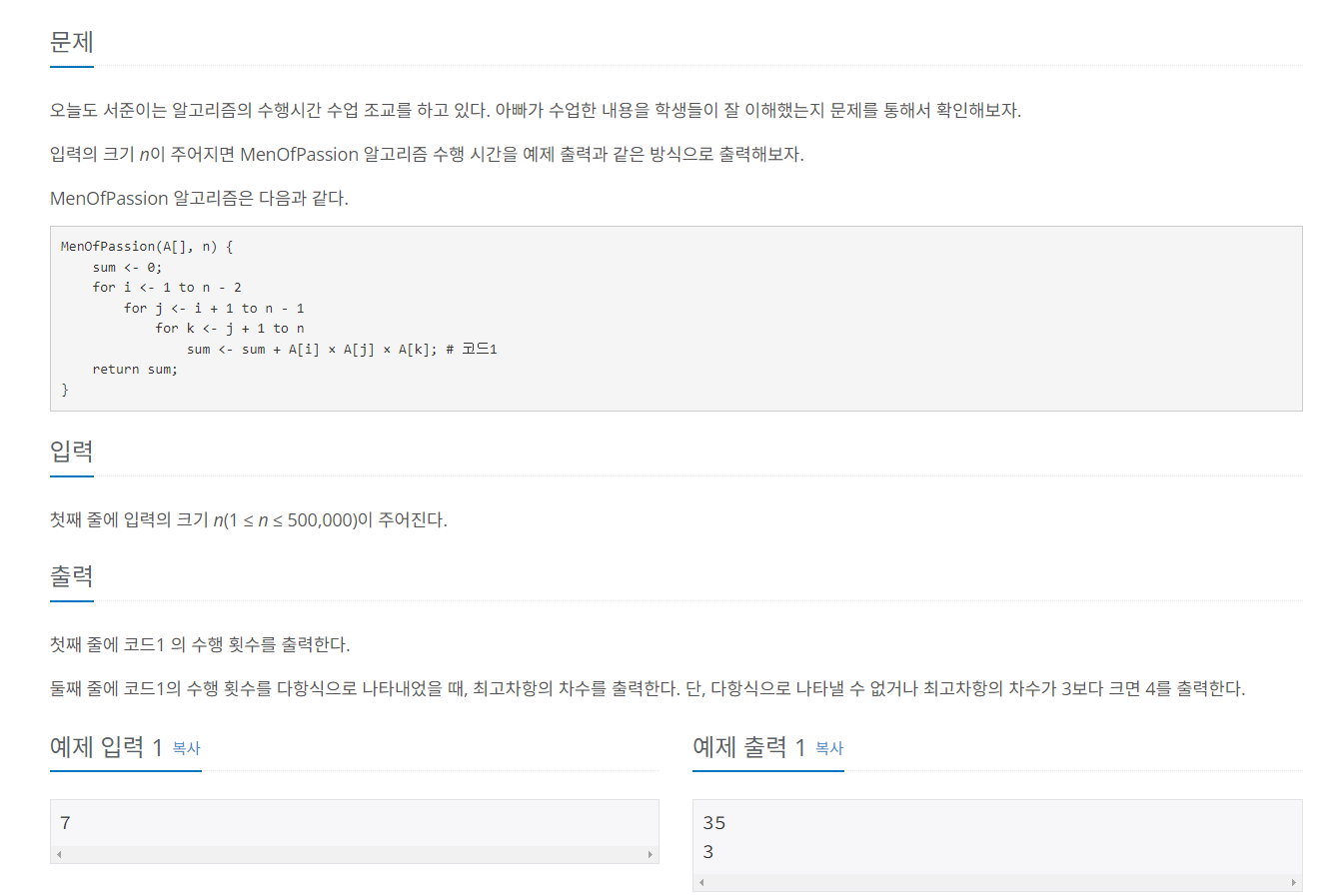
시간 복잡도에 관한 문제입니다. 규칙은 찾아냈으나 식으로 어떻게 풀어야하는지 어려워 다른분들의 풀이를 보며 도움을 받았습니다!👏

for(i = 1 ~ 5)  //i는 1~5까지 반복
  for(j = 2 ~ 6) //j는 2~6까지 반복  
    for(k =  3 ~ 7) //k는 3~7까지 반복

• N = 7 일때 반복하는 과정은 수행횟수는 i를 기준으로
  15 -> 10 -> 6 -> 3 -> 1 번 반복하여 총 35회를 나타나게 됩니다.
• 반복횟수는 점차 -5, -4, -3, -2로 줄어들고 있습니다.

위에는 제가 찾아낸 규칙입니다. 이것만으로도 문제는 해결할 수 있겠지만, 좀더 효율적인 방법이 없을까 고민하였습니다.
결과적으로 고등학교 학창 시절에 배웠던 조합 공식을 사용하는 방법을 찾아냈습니다.

조합공식(nCr)

조합이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)

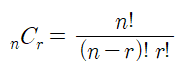
• n : 최대 몇까지의 숫자인지
• r : 뽑아야하는 숫자의 개수

이 공식을 어떻게 활용할까요?
이번 문제의 반복문에서는 서로 중복되는 값이 없습니다. N이 7을 입력받았다고 가정하면

#반복과정
for(i = 1 ~ 5)  //i는 1~5까지 반복
for(j = 2 ~ 6) //j는 2~6까지 반복  
for(k =  3 ~ 7) //k는 3~7까지 반복

#i가 1이고 j가 2일때
1.(i=1, j=2 , k=3) 
2.(i=1, j=2 , k=4)
3.(i=1, j=2 , k=5) 
4.(i=1, j=2 , k=6) 
5.(i=1, j=2 , k=7)

#i가 1이고 j가 3일때
1.(i=1, j=3 , k=4)
2.(i=1, j=3 , k=5) 
3.(i=1, j=3 , k=6) 
4.(i=1, j=3 , k=7)

...
..
.
(생략)

위의 과정을 보면 i와 j와 k 조합의 중복이 이루어지지 않는다는것을 확인할 수 있습니다.
때문에 조합공식을 사용할 수 있습니다!!!
저희는 7을 입력받았다고 과정했을때 최대7개 중에서 3개의 수로 만들수 있는 조합을 구해야하기 때문에 7C3을 구해야합니다. (n = 7, r = 3)

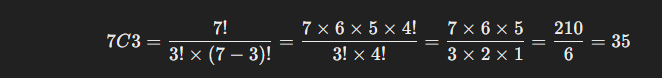
이것을 공식으로 정리하면 아래와 같이 나온다.

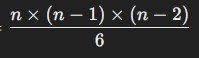
코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());
        long result = ((long) N *(N-1)*(N-2))/6;
        br.close();

        bw.write(result + "\n" + 3);
        bw.flush();
        bw.close();
    }
}