백준 11729 문제 <하노이탑(재귀)>

Frog Lemon·2024년 10월 12일

알고리즘

목록 보기

18/20

서론

하노이탑 문제를 처음 접했을 때, 저 역시 많은 분들이 겪는 것처럼 어려움을 느꼈습니다. 문제 자체는 간단해 보였지만, 그 해결 방법을 떠올리는 것은 결코 쉽지 않았죠. 특히, 재귀 알고리즘을 처음 접했거나 익숙하지 않다면 더욱 그럴 수 있습니다.

문제를 이해하기 위해 우선 저는 하노이탑의 과정을 그림으로 표현해 순서도를 만들어 보려 했습니다. 하지만 초기에는 문제의 본질을 파악하지 못하고 완전히 다른 방향으로 접근해 버렸습니다. 결과적으로 풀이에 큰 혼란을 겪었죠.

그러던 중, 다른 분들의 도움을 받아 여러 글을 참고하고 하노이탑의 기본 원리를 이해할 수 있었습니다. 이 자리를 빌려 감사의 마음을 전하고 싶습니다.😊

하노이탑 알고리즘은 재귀적 사고가 필요한 대표적인 문제로, 그 유명세가 괜히 있는 것이 아님을 깨달았습니다. 하노이탑 문제의 핵심은 큰 문제를 작은 문제로 쪼개는 재귀적 사고에 있습니다. 하지만 이 과정은 처음 배우는 입장에서는 꽤나 어려울 수 있습니다. 저 역시 처음엔 해당 알고리즘의 원리를 전혀 알지 못했기에 풀이를 떠올리기 어려웠습니다.

문제

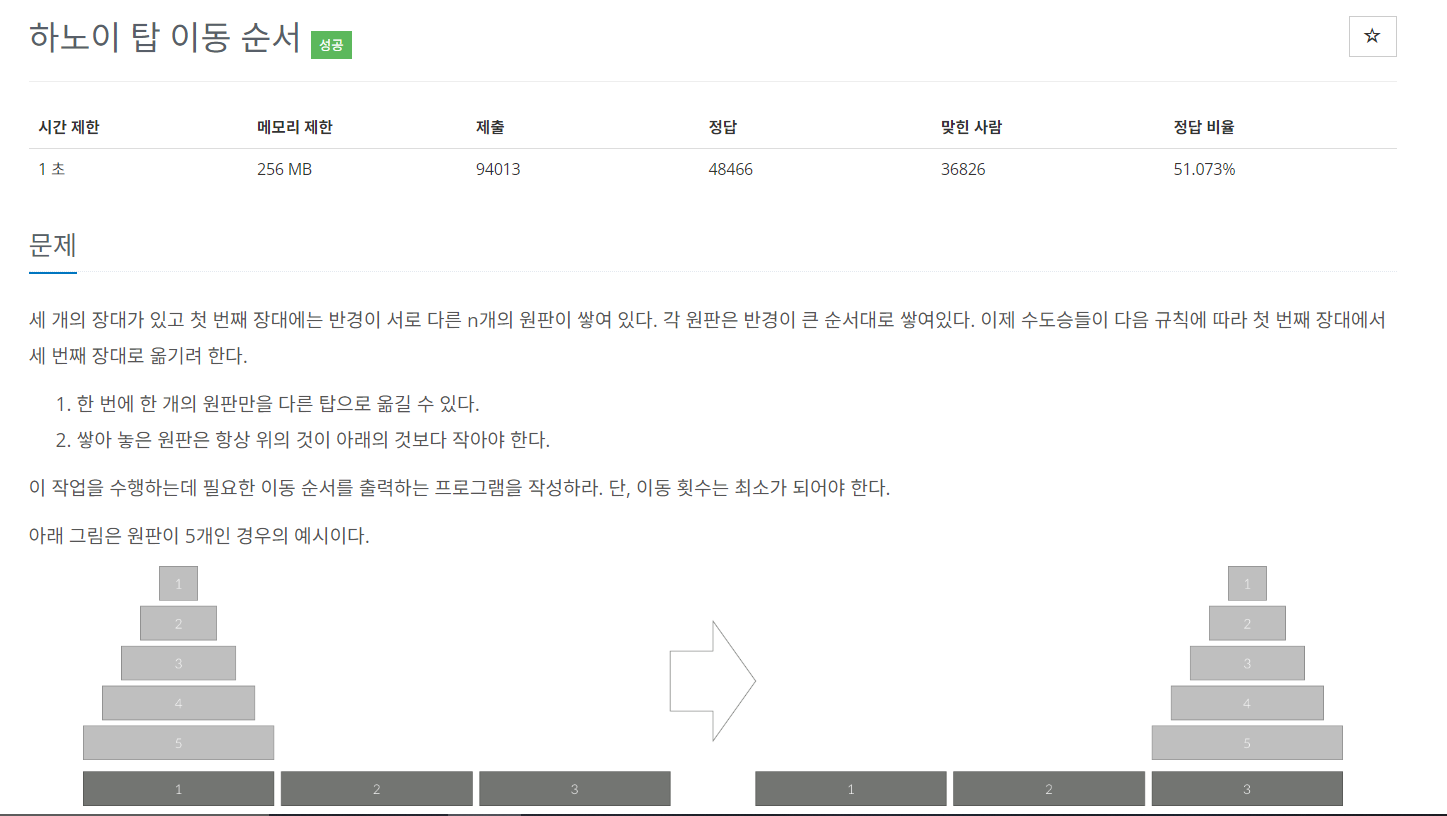
입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.

출력

첫째 줄에 옮긴 횟수 K를 출력한다.

두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.

예제 입력 1

3

예제 출력 1

7
1 3
1 2
3 2
1 3
2 1
2 3
1 3

실패 과정

우선 문제에서 주어진 예제출력을 보고 그림으로 그려 순서를 이해해 보려고 했습니다.

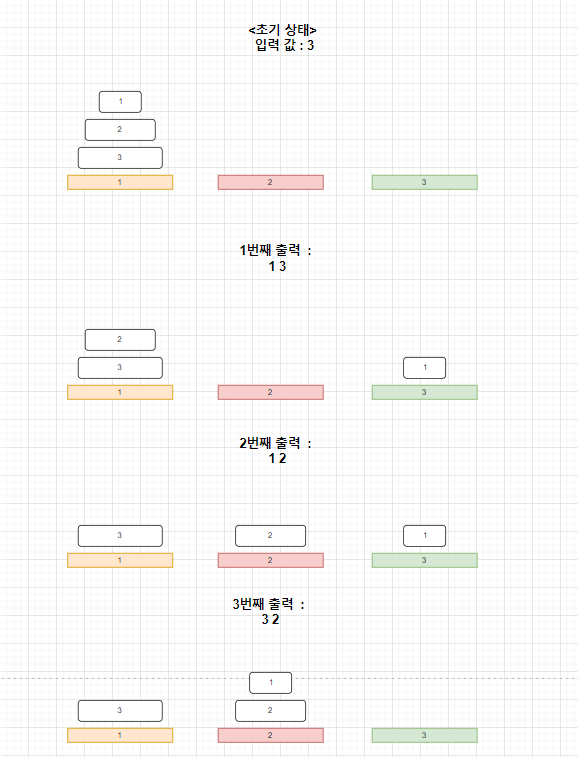
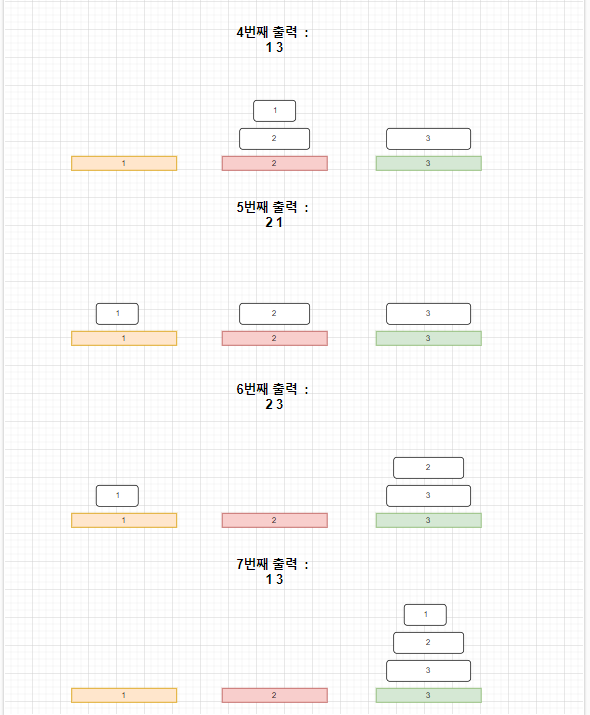
😅 그림을 그리며 이 문제를 시각화하는 것조차도 꽤나 복잡하게 느껴졌습니다.

그래서 문제의 조건을 다시 한번 찬찬히 확인해보았고,

한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다:
→ 즉, 재귀 호출 한 번에 반드시 한 개의 원판만 옮겨야 한다는 것이죠.
출력은 원판이 있던 기존의 탑에서 가장 위에 있는 원판을 목적지의 탑으로 옮기는 것을 의미한다:
→ 이는 반드시 맨 위에 있는 원판부터 차례대로 옮겨야 한다는 조건을 의미합니다.

이 조건들을 보고 "이번 문제는 후입선출 (LIFO: Last In, First Out)의 성질을 갖는 스택 자료구조를을 사용해야 하지 않을 까?"라는 생각이 들었습니다. 그래서 스택과 재귀를 활용한 코드를 짜보았지만, 너무 많은 조건문이 들어갔고, 결국 원하는 결과를 얻지 못했습니다😢.(너무 부족한 점이 많습니다.)

해결 과정

다른 분들의 글을 보고 이해하려고 노력했습니다. 결과적으로 가장 작은 단위가 될 떄까지 재귀로 호출하는 과정을 거칩니다. 문제를 해결하기 위해서는 밑 과정은 세가지로 나뉩니다!

⁜각 탑을 A,B,C라고 한다면 A의 원판들을 C탑으로 옮기기 위해서는 A의 가장 아래있는 원판을 C로 옮겨야한다.

A의 (n-1)개 원판들을 B로 옮긴다. => 이동횟수 hanoi(n-1)
1의 과정이 끝나면 A 맨아래 원판을 C로 옮긴다. =>이동횟수 1
B에 쌓여있는 (n-1)개원판들을 C로 옮긴다. => 이동횟수 hanoi(n-1)

<하노이 메소드>

    private static void hanoi(int N, int start, int mid, int to) {
        count++;
        if (N == 1) {
            sb.append(start+" "+to+"\n");
            return;
        }

        hanoi(N-1,start,to,mid);
        sb.append(start+" "+to+"\n");
        hanoi(N-1,mid,start,to);
    }

N : 원판 갯수
start : 출발지
mid : 중간
to : 목적지

hanoi 메소드 동작 과정

<N == 1일 때>

즉 원판이 하나 남았을 때는 더 이상 분할할 필요가 없습니다.
이때, 현재 위치에서 목적지로 바로 옮기면 됩니다. 코드에서는 sb.append(start + " " + to + "\n");가 이 역할을 합니다.
또한, 이동 횟수를 세기 위해 count++를 추가합니다. 원판 하나를 옮기는 횟수를 기록합니다.

<재귀 호출 (Recursive Case)>

원판이 하나보다 많을 경우, 문제를 세 부분으로 나누어 해결합니다:

첫 번째 과정:

N-1개의 원판을 출발지 start에서 중간 지점 mid로 옮깁니다.
이 때 중간 지점은 목적지 to를 통해서 임시로 옮기게 됩니다.
이를 처리하는 부분이 hanoi(N-1, start, to, mid);입니다. 여기서 목적지와 중간 지점이 바뀐 것이 보입니다.

두 번째 과정:

이제 출발지 start에 남아 있는 가장 큰 원판(맨 아래 원판)을 바로 목적지 to로 옮깁니다.
이때는 sb.append(start + " " + to + "\n");을 사용해 현재 원판의 이동을 기록합니다.
이 과정을 통해 이동 횟수도 기록합니다.

세 번째 과정:

중간 지점 mid에 남아있는 N-1개의 원판을 다시 목적지 to로 옮깁니다.
이때 출발지는 mid, 목적지는 to, 중간 지점은 원래 출발지인 start가 됩니다.
이 과정을 hanoi(N-1, mid, start, to);로 처리합니다.

최종 코드


import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int count = 0;
    static StringBuilder sb;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        sb = new StringBuilder();

        int N = Integer.parseInt(br.readLine());

        hanoi(N,1,2,3);
        System.out.println(count);
        System.out.println(sb);
    }

    private static void hanoi(int N, int start, int mid, int to) {
        count++;
        if (N == 1) {
            sb.append(start+" "+to+"\n");
            return;
        }

        hanoi(N-1,start,to,mid);
        sb.append(start+" "+to+"\n");
        hanoi(N-1,mid,start,to);
    }


}