
💁♀️ 기초 코드 작성 요령
앞으로 코드를 효율적으로, 잘 짜기 위해 필수로 알고 있어야 하는 지식들을 알아보자!
⏰ 시간복잡도?
def func1(arr, n):
cnt = 0
for i in range(n):
if arr[i] % 5 == 0:
cnt += 1
return cnt위 함수는 arr 배열의 원소 중, 5의 배수인 원소의 개수를 출력하는 함수이다.
이 함수는 과연 몇 번의 연산을 수행할까?
💥 연산 : 비트 AND, OR, 비교, 덧셈, 나눗셈, 곱셈, 대입, 함수 호출 등
2번째 줄에서 cnt 변수를 선언하고 0을 넣는 과정에서 1번,
3번째 줄에서 i의 초기값으로 0을 대입할 때 1번,
n번에 걸쳐 i가 n보다 작은지 확인하고, 작다면 1씩 증가시키는 연산 2번,
4번째 줄에서 5로 나눈 나머지를 계산하고 이것이 5와 같은지 비교하는 연산 2번,
5의 배수라면 cnt 값을 증가시키는 연산 1번,
cnt를 반환하는 연산 1번이 추가로 필요하다.
➡️ 1 + 1 + n(2 + 2 + 1) + 1 = 5n+3 번의 연산이 필요하다.
이를 적당히 n번의 연산이 필요하다, n에 비례한다고 이야기한다.
이처럼, 입력의 크기와 문제를 해결하는데 걸리는 시간의 상관관계를 시간복잡도(Time Complexity) 라고 한다.
또, 5n+3 시간복잡도를 적당히 n번의 연산이 필요하다고 말하는 것처럼
주어진 식을 값이 가장 큰 대표항만 남겨 나타내는 방법을 빅오표기법(Big-O Notation) 이라고 한다.
💡 시간복잡도를 표기할 때 보통 빅오표기법의 형태로 나타낸다.
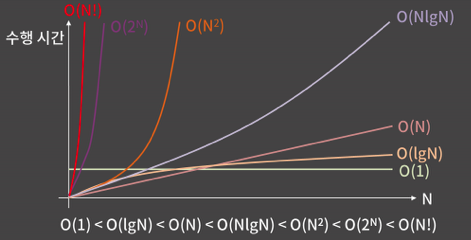
N이 점점 커짐에 따라 시간 복잡도의 차이가 수행 시간에 아주 큰 영향을 미친다.
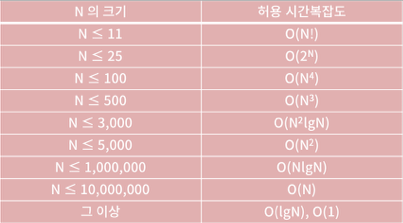
입력의 범위로 문제에서 요구하는 시간복잡도가 어느 정도인지 알 수 있다.
예를 들어, 주어진 배열을 크기 순으로 정렬하는 문제가 있다고 하자.
이 문제는 O(NlogN)으로도 해결할 수 있고, O(N**2)으로도 해결할 수 있다.
N이 1,000 이하라면 둘 중 어느것을 쓰더라도 상관이 없지만, N이 100만이라면 O(NlogN)으로만 해결할 수 있다.
‼️ 주어진 문제를 보고 풀이를 떠올린 후,
그 풀이가 이 문제를 제한 시간 내로 통과할 수 있는지,
내 알고리즘의 시간복잡도가 올바른지 꼭 생각해봐야 한다!
예시 문제의 시간복잡도를 계산해보자.
N이 제곱수이면 1을 반환하고, 제곱수가 아니면 0을 반환하는 함수를 작성하라. N은 10억 이하의 자연수이다.
위 문제의 코드는 아래와 같다.
def exfun(N):
for i in range(N):
if i * i > N:
break
else:
if i * i == N:
return 1
return 0이 방식은 i가 1부터 2, 3으로 커지다 최대 √N까지 올라갈테니,
시간복잡도는 O(√N) 이 된다.
🚪 공간복잡도?
입력의 크기와 문제를 해결하는데 필요한 공간의 상관관계를 공간복잡도(Space Complexity) 라고 한다.
크기가 N인 2차원 배열이 필요하면 공간복잡도는 O(N²) 이고, 배열이 따로 필요없다면 O(1) 이다.
💡 코테에서 대부분의 경우는 공간복잡도보단 시간복잡도 때문에 문제를 틀리는 경우가 더 많다.
( 공간복잡도는 크게 신경쓰지 않아도 된다는 의미..! )
‼️ 코테와 개발은 다르다
코딩 테스트는 남이 알아볼 수 있는, 클린코드를 작성하는 것이 아니다. 제한된 시간 안에 정답을 받아야 한다.
➡️ 코드를 깔끔하게 만들기 위해 노력하기 보다는, 빠르게 짤 수 있는 방식으로 구현하는 것이 훨씬 중요하다!
