Heap, BST

seunghyun·2024년 7월 31일
0

촤라락

목록 보기
2/4

💡 추천하는 분: 알고 있는 내용을 촤라락 정리하고 싶으신 분

힙의 특징들

트리는 계층적 구조를 갖는 데이터를 표현하기 위한 자료구조이고,

힙은 완전 이진 트리(혹은 포화 이진 트리)를 기반으로 한 자료구조이다.

이진 트리 중에서도 마지막 레벨의 오른쪽부분을 제외하고 (왼쪽부터 오른쪽으로 채워지는) 모든 노드가 꽉 찬 이진 트리를 완전 이진 트리라 부른다.

트리는 보통 노드 기반의 연결 리스트로 구현하는데, (케바케)

힙은 완전 이진 트리를 이용하기 때문에 트리 형태의 자료구조임에도 불구하고 배열을 이용하여 구현이 가능하다.

그 이유를 적어보자면,

  1. 새로운 노드를 힙의 '마지막 위치'에 추가해야 하는데, 배열 기반으로 구현해야 이 과정이 수월해진다.

  2. 높이 순서대로 순회하면 모든 노드를 배열에 낭비 없이 배치할 수 있으며 이는 운영체제의 메모리 참조속도에 있어서도 탁월하며 참조의 지역성 및 캐시 히트까지 꾀할 수 있다.

  3. 노드의 개수를 정확하게 계산할 수 있기 때문에 각 노드의 배열상 위치도 정확하게 알 수 있다. 이 특성을 활용하면 배열 인덱스 계산으로 트리상의 자식 노드와 부모 노드를 참조하는 것도 가능하다.

최대 힙과 최소 힙이 있는데, 각 힙은 최대값 혹은 최소값을 상수 시간복잡도로 조회, 삭제할 수 있다는 장점이 있다. 또한 O(logN)의 시간복잡도로 삽입이 보장된다. 최대, 최소 원소를 다루는 특수적인 상황에서 효율적이며 우선순위 큐도 이 힙으로 제작된다.

힙의 조건

힙은 (1) 완전이진트리의 속성을 충족하며

(2) 모든 노드에 대해, 자신의 양쪽 자식 노드보다 크거나 같게(혹은 작거나 같게) 트리의 상태를 유지하는 자료구조이다.

이 상태를 유지 시킨다면 필연적으로 힙의 루트는 최대값 혹은 최소값이 된다.

그렇다면 의문점이 있다. 힙은 원소가 같더라도 서로 다른 구조를 가질 수 있을까?

그렇다. 아래 그림의 힙을 보자.

9 아래에 7, 6이 있는데 두 노드의 위치를 바꾸더라도 힙으로서의 조건을 충족한다. 그러므로 원소의 조합이 같더라도 무수히 많은 구조의 힙이 존재할 수 있다.

(힙의 연산을 그토록 효율적일 수 있었던 건, 이러한 특성이 기반이 되었기 때문이라고 생각한다.)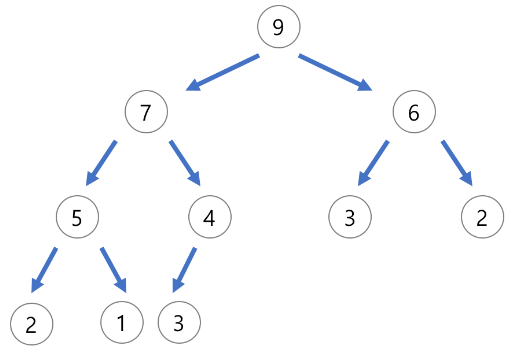

힙 vs BST

BST는 탐색을 위해, 저장과 동시에 정렬을 하는 트리 자료구조이다.

힙과 이진 탐색 트리는 그럼 뭐가 다를까?

둘 다 이진 트리 기반의 자료구조인데 굳이 왜 구분해서 사용할까?!

탐색은 왼쪽 자식은 부모보다 작고, 오른쪽 자식으로 가면 부모보다 크다는 걸 의미한다. (재귀적 연산이 가능함)

즉, 힙과 BST는 자식/부모 간 대소 관계가 다르다는 의미이다!

  1. 이진 탐색 트리는 원소에 중복이 있어서는 안된다. (= 키 값이 유일하다)
    반면 힙은 중복을 허용한다.

  2. 이진 탐색 트리는 정렬된 상태를 유지하지만 (중위 순회하면 정렬된 배열 형태도 얻을 수 있음),
    힙은 정렬되지 않는다.
    즉, 이진 탐색 트리는 균형을 유지하는데에 힙에 비하면 오버헤드가 생긴다.

  3. 이진 탐색 트리는 정렬된 상태가 보장되기 때문에, 중간 어떠한 값이라도 참조할 수 있지만
    힙은 루트에 위치한 값 외에는 참조를 하는 의미가 없다.

  4. 이진 탐색 트리는 O(logN)의 참조, 삽입, 삭제를 지향하지만, 최악의 경우 O(N)까지도 가능하다.
    반면, 힙은 어떠한 상황에서도 깔끔한 O(logN)의 삽입 삭제가 보장되며,
    힙 값 참조에 있어서는 O(1)이 보장된다. (레드블랙트리나 AVL 트리는 O(logN)을 보장한다.)

결론은 최대값, 최소값만 다루는 상황에서는 이진탐색트리보다 힙이 훨씬 유리하다.

연산

삭제 연산
힙: 막내를 이사직에 올린 뒤 강등
BST: 자식이 0개, 1개, 2개일 때마다 각자 다르다

삽입 연산
힙: 신입을 말단에 위치한 후 승진
BST: 대소 비교하며 왼쪽 자식은 부모보다 작고, 오른쪽 자식으로 가면 부모보다 크도록

시간복잡도

값 삽입

  • 배열 : O(1)
  • BST : 평균 O(logN), 최악O(N)
  • 힙 : O(logN)

최대값, 최소값 삭제

  • 배열 : O(N)
  • BST : 평균 O(logN), 최악O(N)
  • 힙 : O(logN)

최대값, 최소값 조회

  • 배열 : O(N)
  • BST : 평균 O(logN), 최악O(N)
  • 힙 : O(1)

BST의 단점

이진탐색트리는 O(logN)의 참조, 삽입, 삭제를 지향하지만, 최악의 경우 O(N)까지도 가능하다.

그래서 중간 삽입, 중간 삭제 연산에 있어서 좀 빠르게 할 수 있게,
트리가 편향되지 않도록 개선하고자 나온 것이 자동정렬/자가균형이진탐색트리이다. AVL Tree와 Red Black Tree가 그 예이다.

C++ STL의 Set, MultiSet, Map, MultiMap은 Red Black Tree를 기반으로 만들어졌다고 한다.
(Unordered_map은 해당하지 않는다! 이 녀석은 해시이다)

힙 구현 C++

코드로 포스트를 마무리해보겠다!

#include <iostream>
#include <vector>
#include <cassert>

using namespace std;
typedef long long ll;

class Heap
{
public:
	Heap(int bucketSize)
		:
		_bucket(bucketSize),
		_heapSize(0)
	{}

	// 힙의 마지막 위치에 새 원소 배치 후 위로 올라가며 힙을 복구한다.
	void Insert(int value)
	{
		int index = _heapSize;
		_bucket[index] = value;
		_heapSize++;

		while (index > 0)
		{
			int parentIndex = (index - 1) / 2;
			int parentValue = _bucket[parentIndex];

			if (parentValue < value)
			{
				std::swap(_bucket[parentIndex], _bucket[index]);
			}

			index = parentIndex;
		}
	}

	// 맨 위 원소를 제거하고, 마지막 원소를 맨 위에 배치 후 아래로 내려가며 힙을 복구한다.
	int Delete()
	{
		assert(_heapSize > 0);

		_heapSize--;
		int ret = _bucket[0];
		_bucket[0] = _bucket[_heapSize];

		int index = 0;

		while (index < _heapSize)
		{
			int lChildIndex = (index + 1) * 2 - 1;
			int rChildIndex = (index + 1) * 2;

			// 양쪽 자식 노드가 모두 현재 노드보다 작으면 현재 위치에 정착한다.
			if ((lChildIndex >= _heapSize || _bucket[lChildIndex] <= _bucket[index]) &&
				(rChildIndex >= _heapSize || _bucket[rChildIndex] <= _bucket[index]))
			{
				break;
			}

			// 양쪽 자식 노드 모두 현재 노드보다 큰 경우, 더 큰 자식과 교체한다.
			if (lChildIndex < _heapSize &&
				rChildIndex < _heapSize &&
				_bucket[lChildIndex] > _bucket[index] &&
				_bucket[rChildIndex] > _bucket[index])
			{
				if (_bucket[lChildIndex] > _bucket[rChildIndex])
				{
					swap(_bucket[index], _bucket[lChildIndex]);
					index = lChildIndex;
				}
				else
				{
					swap(_bucket[index], _bucket[rChildIndex]);
					index = rChildIndex;
				}
			}
			else if (lChildIndex < _heapSize && _bucket[lChildIndex] > _bucket[index])
			{
				swap(_bucket[index], _bucket[lChildIndex]);
				index = lChildIndex;
			}
			else if (rChildIndex < _heapSize && _bucket[rChildIndex] > _bucket[index])
			{
				swap(_bucket[index], _bucket[rChildIndex]);
				index = rChildIndex;
			}
			else
			{
				assert(false);
			}
		}

		return ret;
	}

	int Size() const { return _heapSize; }

	void Print() const
	{
		cout << _heapSize << "   ";
		for (int i = 0; i < _heapSize; ++i)
		{
			cout << _bucket[i] << " ";
		}
		cout << endl;
	}

private:

	vector<int> _bucket;
	int _heapSize;
};


int main()
{

	Heap heap(10);
	heap.Insert(3);
	heap.Print();
	heap.Insert(2);
	heap.Print();
	heap.Insert(1);
	heap.Print();
	heap.Insert(5);
	heap.Print();
	heap.Insert(6);
	heap.Print();
	heap.Insert(4);
	heap.Print();

	while (heap.Size() > 0)
	{
		int value = heap.Delete();
		cout << "pop : " << value << endl;
		heap.Print();
	}

	return 0;
}

부록: Red Black Tree

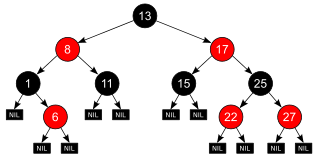
균형을 맞추기 위한 규칙이 5개가 있다.

  1. 노드에 색상을 부여한다. Red 또는 Black으로. (Enum이건 bool이건~)

  2. 루트 노드는 항상 Black 이어야 한다.

  3. Leaf 노드들도 Black 이어야 한다. (더미를 두더라도)

  4. Red 노드의 자식은 항상 Black 이어야 한다. 연속해서 Red-Red 가 등장할 수 없다는 것이다.

  5. 어떤 노드로부터 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 같은 개수의 Black 노드를 만난다.

+) 새로 추가되는 노드는 Red다

profile
seunghyun
game client programmer
이전 포스트

왜 객체 지향을 써야 하는가?

다음 포스트

컴퓨터에서 생성하는 난수는 진짜 난수가 아니다

0개의 댓글