알고리즘이란 무엇인가?
최소한의 효율을 위한 방법을 찾는것이라고 말 할 수 있다.
즉, 컴퓨터 사고를 해야한다는 것이다. 이러한 사고를 키우면 어느 필드에서건 무슨 문제가 닥쳐와도 차근차근 해결해 나가야할 과정을 잘게 쪼개가며 한단계씩 앞으로 나아가 해결해 나갈 수 있는 능력을 가지게 된다니 열심히 키워보자.
자료구조를 잘 알아야 코드의 질이 향상되기에 자료구조의 개념과 활용을 밀접하게 다뤄야 좋은 알고리즘을 짤 수 있다.
좋은 알고리즘의 기준(척도)는 시간복잡도와 공간복잡도 => 시공간 복잡도를 체크한다.
공간 복잡도 S(P)
입력값과 문제를 해결하는 데 걸리는 공간과의 상관관계를 말한다. 입력값이 배가 될수록 공간은 몇배로 늘어나는지
-
프로그램을 실행 및 완료하는데 필요한 저장 공간의 양
-
총 필요 저장 공간
- 고정 공간(알고리즘과 관계 없는 공간): 코드 저장공간, 단순 변수 및 상수를 관리하는 공간
- 가변 공간(알고리즘의 실행과 관련 있는 공간): 코드실행 중 동적으로 필요한 공간
- S(P) = c + Sp(n)
- c: 고정 공간
- SP(n): 가변 공간
-
공간 복잡도는 컴퓨터 저장공간의 기술 발달로 시간복잡도에 비해 상대적으로 중요하지 않음.
=> C언어의 알고리즘을 풀때는 이것도 체크하지만 파이썬과 같은 인터프리터 언어에서는 주로 시간복잡도를 체크한다.
시간 복잡도 (T(n)/O(n))
입력값과 문제를 해결하는 데 걸리는 시간과의 상관관계를 말한다. 입력값이 배가 될수록 시간은 몇배로 늘어나는지
-
특정 알고리즘이 어떤 문제를 해결하는데 걸리는 시간
-
컴퓨터 사양에 따라 시간이 상이할 수 있음
=> 어떤 언어를 사용하는지에 따라서 달라질 때도 있는데 예를들면 파이썬이아닌 파이파이로 선택해서 코드의 시간복잡도를 체크했을때 같은 코드지만 속도는 파이파이가 더 빨랐다.
-
그래서 문제를 해결할 때 성능/시간에 많은 영향을 주는 부분에 대해 시간 예측
- 반복문(연산량)
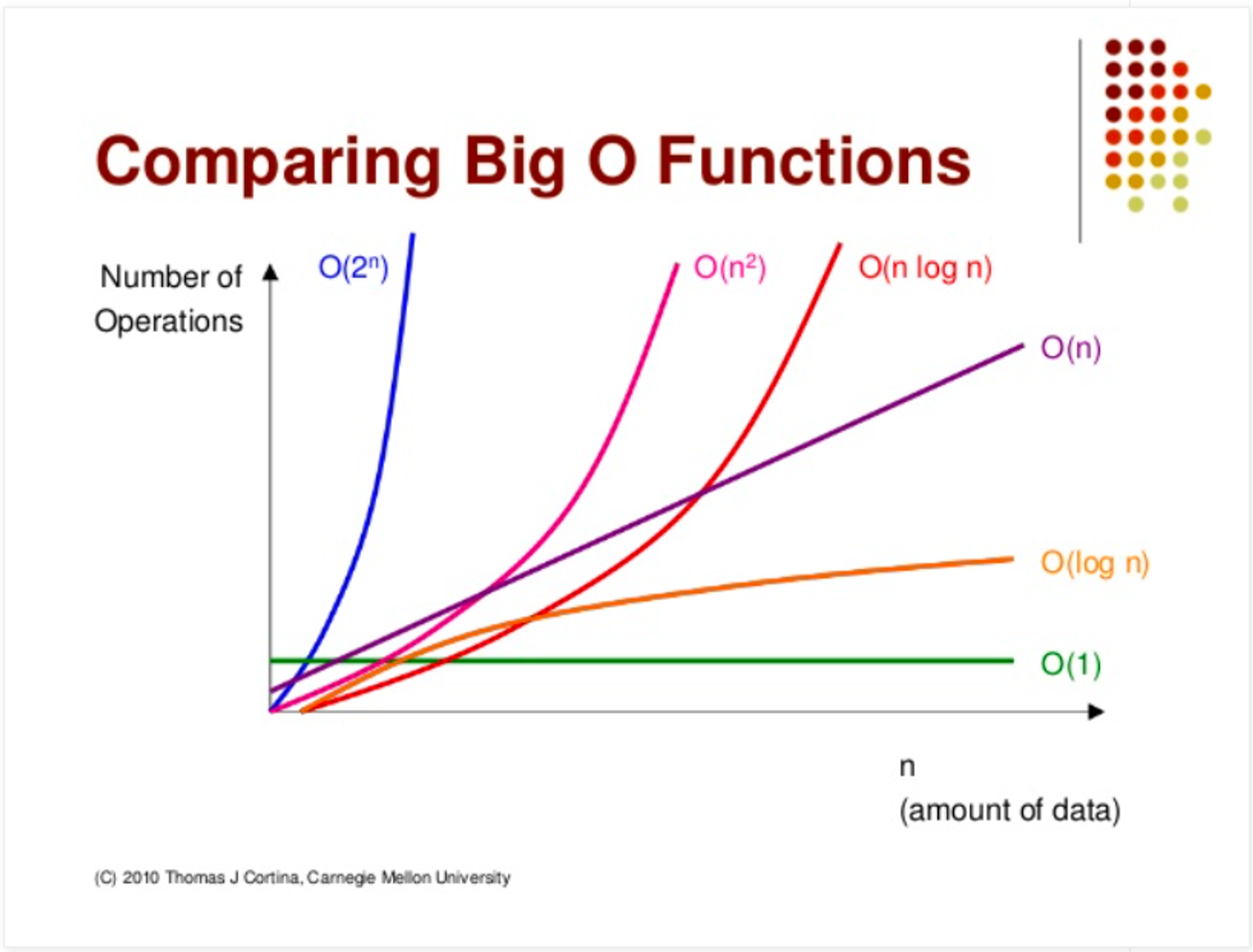
먼저 이러한 효율성을 체크하기위해 점근 표기법이라는것을 활용한다.
<점근 표기법>
알고리즘의 성능을 수학적으로 표기하는 방법으로 알고리즘의 “효율성”을 평가하는 방법이라고 할 수 있다.
점근 표기법의 종류에는
빅오(Big-O)표기법, 빅 오메가(Big-Ω) 표기법이 있는데,
빅오 표기법은 최악의 성능이 나올때 어느 정도의 연산량이 걸릴 것인지 표기
빅오메가 표기법은 최선의 성능이 나올때 어느 정도의 연산량이 걸릴 것인지 표기
- for문을 사용하여 배열[1, 2, 3, 4, 5] 순회
- 빅오메가(Big-Ω): 최선의 경우(1)
- 빅세타(Big-Θ) : 평균(중간)(3)
- 빅-오(Big-O): 최약의 경우 배열의 길이만큼 순회를 해야 함(5)
- 시간 복잡도는 특별한 알고리즘 제외 주로 빅-오 표기법을 사용
알고리즘에서는 거의 모든 알고리즘을 빅오 표기법으로 분석한다.
왜냐면 대부분의 입력값이 최선의 경우일 가능성은 굉장히 적을 뿐더러,
우리는 최악의 경우를 대비해야 하기 때문이다.
<빅-O 표기법 종류>
1. O(1)(상수 복잡도)(constant complexity)
- 데이터양과 상관없이 항상 일정한 연산량을 갖는 알고리즘/ 그 값이 변하지 않는 항
def fourth_element(arr):
print(f"네 번째 요소는 {arr[3]}임.")
a = [1, 2, 3, 4, 5]
fourth_element(a) # 네 번째 요소는 4임.
b = [23, 4, 6, 34, 86, 85, 24, 2346, 85, 12124]
fourth_element(b) # 네 번째 요소는 34임.
c = [1,23,5,235,23,5,34,6,34,6,43,6,34,6,34,634,6,43,6,3,634]자료량에 상관없이 배열의 인덱스를 사용해서 참조할때는 O(1)라고 볼 수 있다.
2. O(n)(선형 복잡도) (linear complexity)
- 데이터양(n)과 비례해 연산량도 증가하는 알고리즘
for i in range(n):
sum_ += i-
T(n) = xn (x계수)
T(n)은 알고리즘의 실행 시간(기본 연산의 수)
: 입력할 데이터의 양인 n에 대해 계수인 'x' 시간만큼 증가해 걸린다는 것을 의미 -
Big-O : O(n)(계수 제거)
Big-O 표기법에서 중요한 것은 상대적인 성장률이다. 즉, n이 커짐에 따라 함수가 얼마나 빠르게 증가하는지를 나타내는 것이 중요하지만, 그렇다고 해서 구체적인 계수나 더하기 항목을 상세하게 나타내려하는 것은 아니다.
계수 x는 구체적인 구현에 따라 달라질 수 있지만,
Big-O 표기법은 알고리즘의 성장률을 간략하게 표현하기 위한 것이므로 이 계수를 무시합니다.T(n)=3n 의 경우, Big-O 표기법으로는 O(n) T(n)=100n의 경우도, Big-O 표기법으로는 O(n)
즉, 계수 상관무
3. O(n²)(2차 복잡도)(quadratic complexity)
- 데이터양이 증가할수록 데이터양의 제곱만큼 연산량 증가하는 알고리즘
for i in range(n):
sum_ = 0
for j in range(n):
# 2n + n
sum_ += i - T(n) = xn² + n
=> 2차 항의 수식을 따르고 - Big-O : O(n²)(계수 제거)
- 계산에 가장 영향을 많이 미치는 것만 표기/ 가장 빠르게 성장하는 항이 알고리즘의 성장률을 결정
-
n² + 2n + 100
-
O(n)²
=>제곱, 세제곱 등의 고차 항이 가장 빠르게 성장, 다른 항들(선형 항, 로그 항, 상수 항 등) 은 큰 n값에 대해 상대적으로 무시한다.O(n^3): 삼차 복잡도 (cubic complexity)
.
.
-
4. O(log n) (로그 복잡도)(logarithmic complexity)
-데이터양(n)이 반으로 줄여나가며 연산량을 감소시키는 알고리즘
-지수 2를 ‘몇 번’ 곱해야 n이 되는지를 알고자 할 때 ‘몇 번’을 계산하는 것
-로그(log) 함수는 지수 함수의 역함수이기에 이 말은 로그 함수의 증가 속도가 매우 느리다는 것을 의미할 수 있다.
-로그 증가는 매우 느리므로, 입력 크기가 커져도 로그 복잡도를 가지는 연산의 증가는 상대적으로 느립니다.
느리게 증가한다는 의미는
예를 들어:
n이 16일 때, log₂n은 4입니다.
n이 1,000,000일 때, log₂n은 대략 20입니다.
[더 간단하게 보자면:]
n이 1000일때 log₂n(1000) ≈ 10 => 최대 10번의 연상이 필요, 약 10의 결과가 나오니.
2000개로 늘어나면, 이진 검색에서는 단지 1회의 추가 연산만 필요합니다. (즉, 11번의 연산)
4000개로 늘어나도, 이진 검색에서는 12번의 연산만 필요합니다.
=> n의 값이 2배로 늘어날 수록 1번의 연산만 더 커지게 되는것이다. -입력 크기가 큰 경우에도 로그 복잡도의 연산 횟수는 그리 크게 증가하지 않습니다. 반면, 선형 복잡도는 입력 크기에 직접적으로 비례하여 연산 횟수가 증가합니다.
즉, 입력 크기가 2배로 증가하면 연산의 수도 2배로 증가합니다. 반면 로그 복잡도에서는 입력 크기가 2배로 증가해도 연산의 수는 1만큼만 증가하게 됩니다.
예를 들어:
n이 16일 때, 최악일결우 16번 연산을 수행해야합니다.
n이 1,000,000일 때, 1,000,000번 연산을 수행해야합니다.따라서, 만약 알고리즘이 O(log n)의 복잡도를 가진다면, 이는 큰 입력에 대해서도 매우 효율적으로 동작할 가능성이 높습니다.
- 이진(binary search)검색 알고리즘이 좋은예. 각 단계에서 반으로 검색범위를 줄여나가는 알고리즘
-이진검색을 사용하려면 대상의 배열이 미리 정리가 되어있는 상태여야 옳바른 값을 가질 수 있다.
-이진검색의 기본원친은 중간 값으로 타켓값을 비교하고 타겟 값이 중간 값보다 작으면 왼쪽 하위배열로, 크면 오른쪽 하위배열을 검색하기 때문에 이런 방식으로 탐색하려면 배열이 오름차순 또는 내림차순으로 정렬이 되어있어야한다. => sorted()함수는 Timsort라는 알고리즘을 기반, 그것의 시간복잡도는 최선의 경우 선형복잡도(O(n) 평균과 최악의 경우 선형 로그 복잡도(linearithmic complexity)를 가지게된다.
-배열이 옳바르게 순차적으로 정렬되어 있지 않으면 선형로그복잡도를 가진 병합정렬의 코드를 갖게된다.
로그복잡도의 코드 예시
def binary_search(arr, x):
"""
Returns the index of x in arr if present, else -1.
"""
# Define the initial search boundaries
left, right = 0, len(arr) - 1
while left <= right:
# Find the mid index
mid = (left + right) // 2
# If x is the middle element, return its index
if arr[mid] == x:
return mid
# If x is smaller, it can only be present in the left subarray
elif arr[mid] > x:
right = mid - 1
# Else the element is in the right subarray
else:
left = mid + 1
# If we reach here, then the element was not present in the array
return -1
# Example usage
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
x = 7
# Function call
result = binary_search(arr, x)
if result != -1:
print(f"Element {x} is present at index {result}")
else:
print(f"Element {x} is not present in the array")5. O(nlogn): 선형 로그 복잡도 (linearithmic complexity)
-데이터의 각 요소에 대해 작업을 수행하는 동안 데이터를 로그 적으로 줄여나가는 과정을 반복한다는 것을 의미
-분할 정복(divide and conquer) 전략을 사용하는 알고리즘들에서 자주 나타난다.
-대표적인 예는 병합 정렬(merge sort)이나 퀵 정렬(quick sort) 같은 정렬 알고리즘들.
-분할 : 배열을 두 개의 동일한 크기의 하위 배열로 반복적으로 분할
-예를 들어, 크기가 8인 배열이 있다면, 이는 4의 크기를 가진 두 개의 하위 배열로 분할되며, 이 두 하위 배열은 각각 크기 2의 두 개의 하위 배열로 또 분할됩니다. 이 과정은 배열의 크기가 1이 될 때까지 반복됩니다.
-O(log n)의 시간복잡도를 가짐 -> 배열의 크기가 반으로 계속 줄기 때문이다.
-정복 : 크기가 1인 배열은 자체적으로 정렬되어 있다고 간주-> 분할된 작은 배열들을 다시 병합하면서 정렬 -> 하나의 정렬된 배열로 만드는것.
-모든 원소에 대한 병합 작업이 이루어집니다. 따라서 각 단계는 O(n)의 시간 복잡도를 가집니다.
-선형(n)부분(병합 단계 (Merge Step)은 데이터의 모든 요소에 대해 일을 수행한다는 것을 의미하고, 로그(log2n)부분은(분할 단계 (Divide Step):데이터를 반으로 나누는 동안 수행되는 작업이나,
선형 로그복잡도의 코드 예시
```
def merge_sort(arr):
# Base case: If the array has one or zero element, it's already sorted
if len(arr) <= 1:
return arr
# Divide the array into two halves
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
# Recursively sort both halves
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
# Merge the sorted halves
return merge(left_half, right_half)
def merge(left, right):
result = []
left_index, right_index = 0, 0
# Traverse both left and right arrays
while left_index < len(left) and right_index < len(right):
if left[left_index] < right[right_index]:
result.append(left[left_index])
left_index += 1
else:
result.append(right[right_index])
right_index += 1
# If left array still has elements, add them to result
while left_index < len(left):
result.append(left[left_index])
left_index += 1
# If right array still has elements, add them to result
while right_index < len(right):
result.append(right[right_index])
right_index += 1
return result
# Example usage
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print(sorted_arr) # Expected output: [3, 9, 10, 27, 38, 43, 82]재귀함수 merge_sort()를 통해서 요소가 1나씩남을때까지 돌다가 1나가 남게되면 return(arr)을 하면서 그 실행이 끝이나고 (재귀함수이기 떄문에 무한루프가 되지않도록 끊어주는 역할을 하는것), 이 return(arr)가 mid = left_half이 부분으로 돌아가면서 return(merge()) 단계로 돌아가 계속 처음으로 나눠진 시점까지 돌아가서 나눠지게 되는것이다. 그리고 나서 arr를 merge함수를 통해 다 정렬시키고 sorted된 result arr를 반환.
즉, 1개씩 남아있을때 return(arr)를 재귀함수를 끝내고, 이전 단계인 merge()로 들어가면서 맨 첫번째의 return (merge())의 값을 반환하게 된다. 이전의 return값은 의미가 없어지는건 아니고 조금씩 sort해서 merge한 값을 반환해주고 merge_sort에 달라진값으로 매개변수로 들어가는 것이다.
예를 들어 리스트에서 left_side [38,27,43]=>
[38,27]vs[43]으로 나뉘고
right_side 재귀하려해도 1로 남게 되니까 기다렸다가
또 left_side 머지 부분으로 가서 [38],[27]의 순서를 정리하고,
left_side가 그 전 단계로 돌아와서 merge()파트를 실행하고
left_side의 머지한 부분의 값은 정돈되어 받아서 [27,38]
right_side[43]와 나눠진 왼쪽 부분의 최종 merge() => result에 [27,38,43]이 이 남게 되고
맨처음 나눠진 right_side부분은 [3,9,82,10]가
left_side[3,9] right_side부분은 [82,10]로 나눠져서
left_side : left_side[3],right_side부분은 [9] merge()=> [3,9]
right_side: left_side[82],right_side부분은 [10] merge()=> [10,82]
와서 [3, 9, 10, 82] 가 최종 오른쪽 merge()의 값으로된다.
그 이후 최종 right_side [3, 9, 10, 82] 와 left_side[27,38,43]의 merge()를 실행해
최종 값=> [3, 9, 10, 27, 38, 43, 82] 나오게 된다.
재귀함수의 이해를 잘 해야되는게 일단 return될때까지 돌다가 리턴되면 그 리턴된 재귀된기 전에 순서로 돌아와 받아 온값을 변수에 저장하고 그 값을 가지고 그 밑에 있는 코드를 실행하고 또 그렇게 return이되면 그전으로 돌아와 실행을 하게되는것.
재귀함수가 동시에 2개가 있으면 2개다 동시에 실행다가 마지막에 만나 마무리된다.
