TIL
- PS : 파괴되지 않은 건물 - 누적합 알고리즘
- JAVA 8부터 메모리 구조가 달라졌다고
1. 파괴되지 않은 건물
board 매개변수에 건물들의 강도가 기록된 2차원 배열이 주어진다. 행과 열의 길이는 최소 1, 최대 1,000이다. 그리고 skill 매개변수에 최소 1, 최대 250,000 길이를 가진 [type, r1, c1, r2, c2, degree] 형태의 배열들이 주어진다. type에는 해당 skill 원소가 공격인지 여부, (r1,c1)과 (r2,c2)는 공격 및 회복 스킬의 범위(각각 왼쪽 위~오른쪽 아래), degree는 파괴와 회복 스킬의 강도를 결정한다.
skill 길이만큼의 공격/회복이 일어났을 때, 파괴되지 않은 건물 즉 board의 값이 1 이상인 건물의 개수를 구해야하는 문제이다. 정확성과 효율성 각각 점수가 따로 있다길래 직감했다. 구현만 해선 안되겠구나!
일단 무식하게 구현만 된 파이썬 코드이다. 너무 단순해서 설명하기도 민망할 정도다! 정확성 테스트는 만점이지만, skill 리스트의 원소가 25만, board가 1000 * 1000이어서 100만개 원소를 가질 경우 2500억이라는 듣도보도 못한 시간 복잡도를 가지게 된다.
def solution(board, skill):
answer = 0
for isAttack,r1,c1,r2,c2,degree in skill:
for r in range(r1,r2+1):
board[r][c1:c2+1] = [board[r][c]-degree for c in range(c1,c2+1)] if isAttack==1 else [board[r][c]+degree for c in range(c1,c2+1)]
for r in range(len(board)):
for c in range(len(board[0])):
answer = answer + 1 if board[r][c]>0 else answer
return answer시간 안에 풀고 싶다면, 이 문제는 다르게 접근해야한다. 결론부터 말하자면 누적합 알고리즘을 알아야한다.
누적합은 엄청나게 큰 배열 범위에 엄청나게 많은 덧셈 연산을 해야할 경우 빛을 발한다. 배열에 덧셈을 시킬 때 접근 시간을 획기적으로 줄여주기 때문이다. 엄청나게 긴 배열의 i~j 인덱스에 특정 수 k를 더한다고 생각해보자. 두 인덱스 사이 원소를 N개라고 가정하고, 총 M번 수를 더한다면 일반적으로 생각해볼 수 있는 시간 복잡도는 O(NM)이 된다. 시간 복잡도를 더 줄일 방법이 없을까?
M번 들어온 연산에 대해선 어떻게 할 수 없다. 배열의 각 원소 접근 시간인 O(N)을 줄여야 한다. 이를 위해 누적합에선 다음과 같은 과정을 거친다.
- 모든 원소가 0으로 초기화된 배열을 하나 만든다. 이 배열은 오로지 합을 저장하기 위한 배열이다.
- 합을 저장하기 위한 배열에 하는 작업이다. 덧셈의 시작 인덱스인
i에k를 더하고, 덧셈의 끝 인덱스의 바로 다음 인덱스인j+1에-k를 더한다. - 덧셈이 일어나는 만큼 위 과정을 반복한다.
- 덧셈이 끝나면 자신의 바로 앞 인덱스 원소와 자신을 더하는 누적합 프로세스를 시작한다.
- 마지막으로 원래 배열과 합을 저장한 배열을 더한다. 원하는 결과가 나온다.
이렇게 했을 경우 M번의 덧셈에 대해 2번 과정이 한 번씩만 일어나므로, N이 얼마나 크든 실제 덧셈을 표시하는 시간은 O(1)이 된다. 4번 누적합을 구하는 과정에서만 전체 배열을 O(N)시간에 돌기 때문에 원래 누적합을 이용한 알고리즘의 시간복잡도는 O(M+N)이 된다.
이게 된다고? 예시를 들어보자. [1,2,3,4,5,6] 배열의 1~3번 인덱스에 n을 더하고, 3~4번 인덱스에 2n을 더하고 싶다. 두 번의 덧셈 결과는 [1,2+n,3+n,4+3n,5+2n,6]이 되어야 한다. 과연 누적합을 했을 때와 같을지 과정을 따라가보자!
[0,0,0,0,0,0,0]으로 초기화된 배열을 하나 만들었다. 배열 크기가 1이 더 큰 이유는 덧셈 인덱스의 범위가 맨 끝 인덱스일때를 대비해서다.- 1~3번 인덱스에 n을 더하는 과정이다. 1번 인덱스에 +n, 4번 인덱스에 -n을 한다. 결과는
[0,n,0,0,-n,0,0]. - 3~4번 인덱스에 2n을 더하는 과정이다. 3번 인덱스에 +2n, 5번 인덱스에 -2n을 한다. 결과는
[0,n,0,2n,-n,-2n,0]. - 누적합 프로세스이다. 합을 저장하는 배열에서 i번째 원소는 자신과 i-1번째 원소를 더한 값이다. 결과는
[0,n,n,3n,2n,0,0]. - 마지막으로 원래 배열과 합을 저장한 배열을 합한다. 합을 저장한 배열의 가장 끝 인덱스는 버린다. 결과는
[1,2+n,3+n,4+3n,5+2n,6].
원하는대로 결과가 잘 나왔다! 실제로 알고리즘을 알아보면서 이게 되겠냐 ㅋㅋ 했는데 이게 됐다.
누적합을 구하기 위해 0으로 초기화된 배열을 하나 만들고 더하고자 하는 첫번째 인덱스와, 마지막 인덱스+1 각각에 n과 -n을 해주는건 알겠다. 문제는 '파괴되지 않은 건물'의 2차원 배열에서 발생한다. 2차원 배열에서의 누적합? 갑자기 머리가 새하얘진다. 여기는 한 번만 더 응용을 해주면 된다.
문제처럼 (r1,c1)(좌측상단)부터 (r2,c2)(우측하단)까지의 범위에 수를 더한다면.. 각 모서리를 기준으로 좌측상단인 (r1,c1)에 +n, 우측 상단보다 한 칸 오른쪽인 (r1,c2+1)에 -n, 좌측 하단보다 한 칸 아래인 (r2,c1+1)에 -n, 우측 하단보다 우측 하단으로 한 칸 떨어진 (r2+1,c2+1)에 +n을 해주면 된다. 요컨데 행과 열을 기준으로 각각의 인덱스 범위 바깥에 -n을 해주는 것이다. 그 뒤 행과 열을 기준으로 각각 누적합을 돌면 된다.
예를 들어, 3*3 배열에서 (1,1) 인덱스부터 (2,2)인덱스까지 n을 더한다 생각해보자. 그렇다면 누적합을 저장할 배열을 4*4로 초기화하고, n을 더할 인덱스에 대해 다음과 같이 설정한다.
0 0 0 0
0 n 0 -n
0 0 0 0
0 -n 0 n이 뒤, 같은 행을 기준으로 쫙! 누적합을 돌고, 같은 열을 기준으로 쫙! 누적합을 돌면 된다. 일단 같은 행을 기준으로 누적합을 돌자.
0 0 0 0
0 n n 0
0 0 0 0
0 -n -n 0마지막으로 같은 열을 기준으로 누적합을 돌자.
0 0 0 0
0 n n 0
0 n n 0
0 0 0 0원하는대로 (1,1)부터 (2,2)까지 n이 더해져있다. 이걸 어떻게 아나요!!!!
알고리즘을 알면 구현은 간단하다. 합을 담을 accum 리스트를 만들어놓고, skill 리스트에 나온 각 덧셈에 대해 합 표식을 한다. 각 행과 열으로 누적합을 돌고, 원래 리스트 값과 합쳐서 0보다 큰지 여부를 조사하여 답으로 내놓으면 된다.
def solution(board, skill):
answer = 0
n,m = len(board),len(board[0])
accum = [[0 for _ in range(m+1)] for _ in range(n+1)]
for isAttack,r1,c1,r2,c2,degree in skill:
degree = -degree if isAttack==1 else degree
accum[r1][c1] += degree
accum[r2+1][c1] -= degree
accum[r1][c2+1] -= degree
accum[r2+1][c2+1] += degree
for x in range(n+1):
for y in range(1,m+1):
accum[x][y] += accum[x][y-1]
for y in range(m+1):
for x in range(1,n+1):
accum[x][y] += accum[x-1][y]
for x in range(n):
for y in range(m):
if (board[x][y] + accum[x][y]>0):
answer += 1
return answer이걸 실제 시험때 시간복잡도까지 고려해서 푼 사람들은 존경받아 마땅하다.
2. JAVA 8부터 JVM 힙 메모리 구조가 달라졌다고!
2-1) 기존 JVM heap
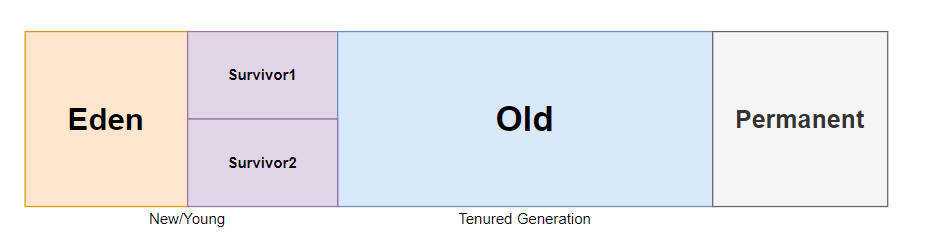
보통 자바 관련 기본서에 나와있는 JVM의 힙 영역이다. 위에서 GC의 대상이 되지 않는 것은 Permanent 영역 뿐이다. Permanent 영역엔 다음과 같은 항목들이 저장된다.
static키워드가 붙은 상수 및 변수- class 및 method의 meta data
- JIT, JVM 관련 meta data
- String Constant Pool
요컨데 정적 변수와 각종 메타 데이터가 들어있다. new를 통해 생성되는 보통의 객체와 다르게, 자바 프로세스 전반적/전역적으로 사용되는 변수들이 위치하는 것 같다.
2-2) 바뀐 JVM
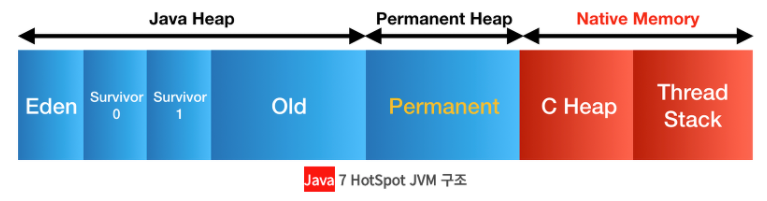
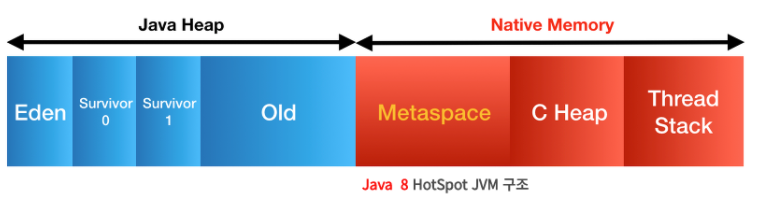
Permenant가 사라지고 Metaspace로 대체되었다. Metaspace는 Native Memory 영역이다.
- Native Memory : 자바 프로세스 메모리에 해당하는 Heap과 다르게 OS가 관리하는 메모리 영역. 기존의 Permanent 영역보다 훨씬 큰 공간의 메모리를 사용할 수 있다.
이로써 기존에 Permanent에 있던 요소들이 여기저기로 옮겨지게 됐다.
- class 및 method의 meta data : Metaspace로 이동
static키워드가 붙은 상수 및 변수 : Heap으로 이동- String Constant Pool : Heap으로 이동
- JIT, JVM 관련 meta data : Metaspace로 이동
2번을 보면 알 수 있는데, 과거의 그것과는 달리 static 키워드가 붙은 변수나 상수 역시 GC의 대상이 되었다.
2-3) 왜 이런 짓을?
java 8 전까지 Eden~Permanent의 힙 주소공간은 JVM이 가지고 있는 메모리이기 때문에, 메모리 관리가 자바 프로세스 안에서 진행됐다. 때문에 자바 프로세스에 할당된 메모리 크기 이상은 사용할 수 없었다.
GC도 되지 않는 제한된 Permanent 메모리 공간 안에서, static으로 된 객체를 많이 사용하거나 객체의 크기가 크다면 OOM(Out Of Memory) 에러가 나곤 했다.
때문에
static자료형 역시 GC의 대상이 될 수 있도록 하고- Permanent에 들어갔던 meta data들을 OS가 관리하는 공간으로 넘겨
앞서 고려해야했던 OOM 이슈를 최소화했다고 볼 수 있다.
REFERENCE
https://1-7171771.tistory.com/140
https://mirinae312.github.io/develop/2018/06/04/jvm_gc.html
