6. Local Descent

김재희·2021년 8월 26일
0

최적화 이론

목록 보기
5/9

0. Descent Direction Iteration

이 장에서는 국지적으로 근사한 모델을 통해 목적함수를 최소화하는 방향으로 반복적으로 조금씩 이동하는 알고리즘들을 살펴보게 될 것이다. 이는 Descent Direction Method라 하며 내가 알고 있는 대표적인 모델은 Gradient Descent인 것 같다. 자세한 사항은 모델마다 다르지만 전반적으로는 다음과 같은 단계를 밟게 된다.

  1. xkx_k(이번 시점의 위치)가 종료 조건을 만족하는지 확인한다.
  2. 그래디언트나 헤시안과 같은 국지 정보를 이용해 이동할 방향과 크기를 담고 있는 벡터 dkd_k를 정한다. 이때, ∣dk∣=1\lvert d_k \rvert = 1일 수도 있고 아닐수도 있다.
  3. 이동할 스텝의 크기 혹은 학습률(learning rate)이라 부르는 αk\alpha_k를 정한다. 어떤 알고리즘은 해당 값이 상수인 스칼라이고, 어떤 알고리즘은 매 반복마다 새로운 값을 계산한다.
    xk+1←xk+αkdk\displaystyle x_{k+1} \leftarrow x_k + \alpha_k d_k

1. Line Search

라인 서치는 descent direction dd가 정해진 상황에서 step factor α\alpha를 최적화하기 위해 사용하는 방법이다. 이때의 목적함수는 다음과 같을 것이다.

minimizeαf(x+αd)\displaystyle minimize_{\alpha} f(x + \alpha d)

여기서 주의할 점은 이미 xx와 dd는 정해진 벡터가 존재하므로 우리는 이제 스칼라 값인 α\alpha에 대한 일변수 최적화를 수행한다는 것이다. 즉, 전체 목적함수는 벡터이므로 다변량 최적화이지만, 부분적으로 라인서치를 사용하면 일변수 최적화를 수행한다.

전체 알고리즘은 다음과 같다. 일종의 수도코드로서 돌아가는지 보장하지 못한다는 점을 유의하자.

import sympy as sp
def line_search(f, x, d):
	alpha = sp.symbol('a')
	obj = f(x + ad)
    a, b = bracket_minimum(obj)
    alpha = minimize(obj, a, b)
    return x + alpha*d

여기서 bracket_minimize 함수는 괄호법으로 대략적인 국지적 최소값의 범위를 잡아주는 함수이고, minimize 함수는 a, b 범위 내에서 해당 함수를 α\alpha에 대해 미분을 수행해주는 함수이다.

하지만 이런 식으로 진행하게 되면 함수에 대한 미분에서 많은 연산량을 요구하게 된다. 이는 높은 정확도를 가지지만 시간이 오래 걸릴 수 있기 때문에, step factor를 고정하여 learning rate으로 사용하기도 한다.

Learning Rate Decay
하지만 learning rate을 상수로 고정하게 되면 다음과 같은 문제가 생길 수 있다.

  • lr의 크기가 크면 초기에는 빠르게 손실함수 곡선을 타고 들어가면서 optimal point에 근접하지만, 근처에서 overshoot이 지속적으로 발생하여 결국 optimal point에는 도달하지 못하게 된다.
  • lr의 크기가 작으면 convex function의 경우에는 매우 느리게 학습이 진행되어서 optimal point에 도달하는 시간이 너무 길어질 것이다. 혹은 local minima에서 빠져나오지 못하게 된다.

그럼 이 둘을 합쳐서 초기에는 lr을 크게 잡고, 이후 학습이 이루어질수록 학습을 줄이면 좀 더 나은 방법이지 않을까? 이 개념을 도입한 것이 Learning Rate Decay이다. learning rate decay의 학습 시점 t에 대한 업데이트 식은 다음과 같다.

wˉ  ⟸  wˉ−αt∇J\displaystyle \bar{w} \impliedby \bar{w} - \alpha_t \nabla J

이때 αt\alpha_t는 더이상 상수가 아니라 학습 시점 tt에 대한 일종의 함수가 된다. 일반적으로 사용하는 방법으론 exponential decay 와 inverse decay가 있는데 수식은 다음과 같다.

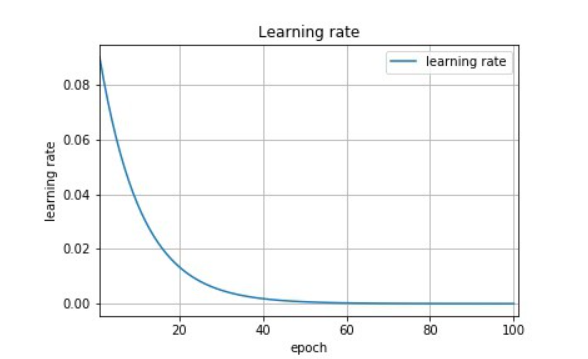
αt=α0(−k⋅t)(Exponential Decay)\tag{Exponential Decay} \displaystyle \alpha_t = \alpha_0(-k \cdot t)
αt=α01+k⋅t(Inverse Decay)\tag{Inverse Decay} \alpha_t = {\alpha_0 \over 1 + k \cdot t}

위와 같이 Exponential Decay와 Inverse Decay 모두 tt에 대해 기하급수적으로 감소하는 모양을 띄고 있다. 이를 통해 초기의 lr은 비교적 크게 잡아 빠르게 손실함수 곡선을 타고 내려가고, optimal point에 근접해지면 lr이 매우 작아지도록 만든다.

2. Approximate Line Search(Armijo Backtracking Line Search)

기존의 line search 방법은 α\alpha가 너무 클 경우 점차 감소하는 방법을 취한다. 하지만 이는 α\alpha가 충분히 작아지도록 만들 수 없다. 이에 Armijo condition과 curvature condition을 추가하여 적당한 α\alpha 값을 찾을 수 있다.
두 조건을 아울러 울프 조건이라 한다. 두 조건을 먼저 살펴보도록 하자.

2-1. Armijo Condition(1차 울프 조건)

아르미요 조건이라 불리는 이 조건은 다음과 같은 수식으로 이루어져 있다.

f(xk+1)≤f(xk)+βα∇dkf(xk)f(x_{k + 1}) \leq f(x_k) +\beta \alpha \nabla_{d_k}f(x_k)

이때, xk+1=xk−βαdkx_{k+1} = x_k - \beta \alpha d_k이므로 위의 식은 다음과 같은 테일러 전개의 1차 미분 항만을 통해 유도되었음을 알 수 있다.

f(xk+1)≈f(xk)+(xk−βαdk−xk)∇dkf(xk)≈f(xk)−βαdk∇dkf(xk)\begin{aligned} f(x_{k+1}) &\approx f(x_k) +(x_k - \beta \alpha d_k - x_k)\nabla_{d_k}f(x_k)\\ &\approx f(x_k) - \beta \alpha d_k\nabla_{d_k}f(x_k)\\ \end{aligned}

이때 그래디언트 디센트에선 dkd_k가 기울기의 반대방향이므로 dk∇dkf(xk)<0d_k\nabla_{d_k}f(x_k) < 0이라는 점을 명심하자. β∈[0,1]\beta \in [0, 1]로 보통 β=1×10−4\beta = 1 \times 10^{-4}로 설정된다고 한다. 이때, α\alpha는 딥러닝에서 사용하는 아주 작은 수가 아니라 10 정도의 큰 수를 의미한다.

위 식은 결국 다음 이동할 지점의 값이 일정 수준이상으로 감소해야 실제로 이동하도록 유도하는 것을 의미한다.

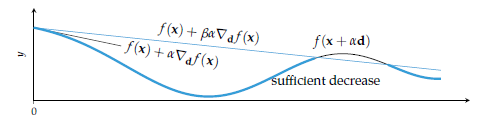
만약 β=0\beta = 0이라면 어느 수준의 감소라도 수용하고 이동하겠다는 것을 의미한다. 위 그림에서 볼 수 있듯이 f(xk)+βα∇dkf(xk)f(x_k) +\beta \alpha \nabla_{d_k}f(x_k)는 현재 지점에 접하면서 하강하는 직선을 형성하게 되고, 다음 이동할 점은 이 직선과 함수 f(x)f(x)의 교점이 된다.

2-2 Curvature Condition(2차 울프 조건)

곡률조건은 다음과 같은 식으로 이루어져 있으며 방향도 함수의 값이 일정수준 이상으로 작아지는 지점으로 이동하도록 한다.

∇dkf(xk+1)≥σ∇dkf(xk)\displaystyle \nabla_{d_k}f(x_{k+1}) \geq \sigma\nabla_{d_k}f(x_k)

이때 β<σ<1\beta < \sigma < 1로 설정되며 얼마나 방향도 함수가 커져야 하는지 요구하는 값을 의미한다. 이때 위에서 언급했듯이 그래디언트 디센트에서 ∇dkf(xk)\nabla_{d_k}f(x_k)가 음수라는 점을 고려하면, 결국 이 식은 다음 지점은 현재 지점보다 일정 수준 이상으로 0에 가까운 값을 가지도록 만든다. 즉, 곡률이 증가하는 방향(2계 도함수의 값이 증가하는 지점)으로 이동하도록 만들어준다. 다른 말로 하면, global minimum에 가까워질수록 현재 지점보다 0에 가까운 방향도 함수값을 가질 수 밖에 없으므로 global minimum에 가까워지게 한다는 것을 의미한다.

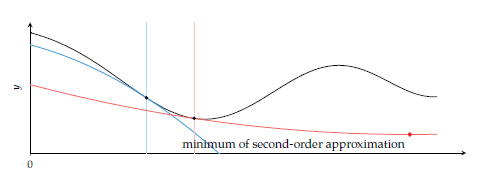
위 조건을 만족하는 다음 지점으로 이동하도록 하는 α\alpha를 찾는 알고리즘을 간단하게 표기하면 다음과 같다. 다음과 같다. 결국 1차 울프 조건은 α\alpha의 상한을 정하고, 2차 울프 조건은 하한을 정하게 된다. 

def backtracking_line_search(f, df, x, d, a, p = 0.5, b = 0.0001, sig = 0.1):
	y, g = f(x), df(x)
    while f(x + a*d) > y + b*a*(g*d): # 1차 울프조건을 만족할때까지 a를 줄임
    	a *= p
    
    x_new = x + a*d
    
    if df(x_new) >= sig*df(x): # 2차 울프조건을 만족하는지 확인 
    	return x_new
profile
김재희
이전 포스트

5. 괄호법(Bracketing Method)

다음 포스트

7. 1계 도함수법(GD ~ Adam)

0개의 댓글