1. 수치미분
최근에서야 딥러닝 모듈이 워낙 잘 되어 있어 역전파에서 오류가 발생할 일은 자주 없다. 특히 개발자나 연구자가 이를 따로 신경쓸 필요가 없다. 역전파에서 오류가 났다면, 모듈이 잘못되었을 가능성보다 코딩에 문제가 있을 가능성이 높을 것이다.
하지만 과거에 인공신경망을 연구하는 사람들은 그렇지 않았다고 한다. BackPropagation의 연산량도 많고, 그 과정도 복잡하여 직접 일일히 코딩을 하거나 해석적 방법을 통해 그래디언트를 계산하다보면, 에러가 발생하게 된다. 진짜 문제는 에러가 나도 코드는 돌아가고, 어디서 문제가 발생했는지 알 수 없다는 점이라고 한다.
이때, 코딩하거나 손으로 계산한 해석 미분(analytical derivatives)이 옳은지 검정하기 위해 사용하는 방법이 gradient checking이다. gardient checking은 기본적으로 수치 미분(numerical derivatives)를 이용한다.
수치 미분은 다음과 같은 식을 이용해 이루어진다.
∂wi∂J(wˉ)≈ΔJ(w1…,wi+Δ,…,wd)−J(w1,…,wi,…,wd)
여기서 Δ는 매우 작은 값으로서 현재의 위치에서 아주 조금 움직이도록 한다. 이는 전방 차분을 이용한 방법인데 테일러 전개를 이용하면 쉽게 증명이 가능하다.
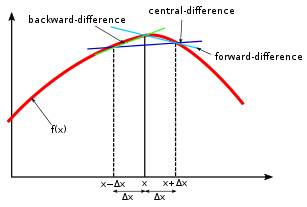
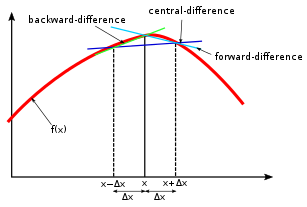
2. 전방, 중앙 차분
충분히 작은 양수 h에 대해 전방, 후방, 중앙 차분은 각각 다음과 같이 정의된다.
D+f(x)=hf(x+h)−f(x)D−f(x)=hf(x)−f(x−h)Df(x)=2hf(x+h)−f(x−h)
이때, 전방 차분의 증명은 다음과 같다.
f(x+h)≈f(x)+hf′(x)+2!h2f′′(x)hf′(x)=f(x+h)−f(x)−2!h2f′′(x)f′(x)=hf(x+h)−f(x)−2!hf′′(x)f′(x)−D+f(x)=−2!hf′′(x)
위 식에서 결국 전방 차분의 오차가 −2!h2f′′(x)구해지게 되는데, 오차가 h에 비례함을 알 수 있다. 후방 차분역시 동일한 과정으로 진행되며, 오차 역시 동일하게 h에 비례한다.
중앙 차분의 경우 아래와 같이 증명된다.
f(x+h)≈f(x)+hf′(x)+2!h2f′′(x)+3!h3f′′′(x)f(x−h)≈f(x)−hf′(x)+2!h2f′′(x)−3!h3f′′′(x)f(x+h)−f(x−h)=2hf′(x)+3!2h3f′′′(x)f′(x)=2hf(x+h)−f(x−h)−3!h2f′′′(x)f′(x)−Df(x)=−3!h2f′′′(x)
이때 중앙차분의 오차는 −3!h2f′′′(x)가 되는데, 결국 h2에 비례한다는 것을 알 수 있다.
이때, h가 충분히 작은(limh→0+) 양수임을 고려하자. 결과적으로 전방/후방 차분은 h에 비례하고, 중앙 차분은 h2에 비례한다는 것을 알 수 있다. 중앙 차분이 추가적인 계산량을 필요로 하지만, 그만큼 훨씬 오차를 줄일 수 있다. 하지만 진동하는 모양의 그래프에서는 중앙차분은 그래디언트가 0이 나올 수 있어 주의가 필요하다.
수치해석을 이용한 gradient checking이 완벽하게 해당 지점의 미분값을 계산할 수는 없지만, 만약 코드나 해석 미분의 값이 잘못되었을 경우에는, 수치 미분의 값과 차이가 커지기 때문에, 무언가 잘못되었을 때 이를 감지하고 수정하기 용이하게 해준다.
여기서 모든 파라미터 wi에 대해 매 레이어마다 이루어져야 하기때문에, 역시 계산량은 많을 수 밖에 없다. 계산량도 많고, 실제 모델에서 역전파가 제대로 이루어지는지 확인하기 위해 사용되기 때문에, 학습 과정에서 항상 사용되지 않는다. 모델의 역전파 과정을 확인하기 위한 디버깅 단계에서 사용된다고 한다.
참고
유한 차분에 대한 위키피디아 페이지