10. 부등식 제약 조건(KKT) & 쌍대성

김재희·2021년 9월 18일
KKT쌍대성최적화
0

최적화 이론

목록 보기
9/9

1. 부등식 제약조건

앞서 등식 제약조건에서 어떻게 라그랑주 승수를 이용해 라그랑지안을 정의하는지 살펴보았다. 그렇다면 부등식 제약조건에서는 어떻게 최적해를 구할 수 있을까?
우선 다음과 같은 부등식 제약 조건이 있다고 생각해보자.

minimizexf(x)subject to g(x)≤0minimize_{\textbf{x}} f(\textbf{x})\\ \text{subject to }g(\textbf{x}) \leq 0

이때 두가지 경우로 나누어 생각해볼 수 있다.

해가 제약조건 경계상에 존재하는 경우

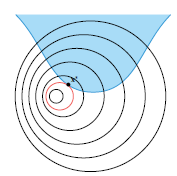
이 경우는 위 그림과 같이 본래 목적함수 ff의 최적해가 제약 조건 바깥에 있어, 제약조건 아래에서는 새로운 최적해가 존재할 경우를 의미한다. 이와 같은 경우는 제약조건이 활성화되었다고 표현하며, 등식제약조건과 동일하게 해를 구하게 된다. 즉, 해가 제약조건 경계에 위치하기 때문에 어떤 상수 μ\mu에 대해 다음처럼 라그랑주 조건이 성립한다.

∇f−μ∇g0\nabla f - \mu \nabla g 0

해가 제약조건 내부에 존재하는 경우

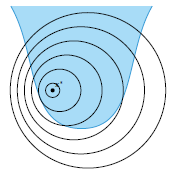
이 경우는 위 그림과 같이 본래 목적함수 ff의 최적해가 이미 제약조건 내부에 존재하기 때문에, 기존의 최적해가 유지된다. 이때는 제약조건이 비활성화되었다고 표현하며, 단순히 ff의 그래디언트가 0이 되는 지점을 찾게 된다.

제약조건에 의해 실현 불가능한 점들이 발생하게 되는데, 이를 무한 스텝 패널티를 이용하여 부등식 제약조건 문제를 최적화하게 된다. 무한 스텝패널티를 도입한 제약조건문제는 다음과 같이 표현된다.

f∞−step={f(x)if g(x)≤0∞otherwise=f(x)+∞⋅(g(x)>0)\begin{aligned} f_{\infin - \text{step}} &= \begin{dcases} f(\textbf{x}) & \text{if }g(\textbf{x}) \leq 0\\ \infin & \text{otherwise} \end{dcases}\\ & = f(\textbf{x}) + \infin \cdot (g(\textbf{x}) >0) \end{aligned}

하지만 무한 스텝 패널티는 최적화하기 쉬운 문제가 아니다. 실현불가능한 점들을 일종의 장벽처럼 만들어놓기 때문에, 불연속적이며, 미분도 가능하지 않다. 즉, 그래디언트를 구할 수 없게 된다.

그래서 제약식을 선형적으로 연결한 선형 패널티를 사용하는데, 이는 다음과 같이 라그랑지안을 구축한다.

L(x,μ)=f(x)+μg(x)L(\textbf{x}, \mu) = f(\textbf{x}) + \mu g(\textbf{x})

이때, μ>0\mu >0는 목적함수에 패널티를 부여하여 실현불가능한 영역에 대해 무한 스텝 패널티에서의 ∞⋅(g(x>0))\infin \cdot (g(\textbf{x} >0))의 하계를 형성하는 역할을 하게 된다.

이는 다음과 같이 μ\mu에 대해 라그랑지안을 최대화하여 무한스텝패널티를 복구하는데 이용된다.

f∞−step=maximizeμ≥0L(x,μ)f_{\infin - \text{step}} = \text{maximize}_{\mu \geq 0} L(\textbf{x}, \mu)

이는 gg가 0보다 큰 지점에 대해서는 실현불가능한 지점을 명확하게 짚어주고, gg가 0보다 작거나 같은 실현가능한 지점에 대해서는 본래의 최적해를 찾을 수 있도록 도와주는 역할을 하게 된다.
이에 대해 조금 더 설명하자면, maximizeμ≥0f(x)+μg(x)\text{maximize}_{\mu \geq 0} f(\textbf{x}) + \mu g(\textbf{x})는 결국 g>0g>0인 구간에 대해서는 μ\mu를 키워 제약 조건 아래에서 최적해를 가지지 않도록 하고, g<0g < 0인 구간에 대해서는 μ=0\mu = 0이 되어 제약 조건의 범위 안에서 최적해가 존재하도록 만들어 준다. 즉, 실현불가능한 구간에 대해서는 무한대의 값이 나오고, 실현가능한 구간에 대해서는 f(x)f(\textbf{x})의 값을 얻으면서도 연속이면서 미분가능한 함수를 얻은 것이다.

이제 최적화 문제를 새롭게 정의할 수 있게 되었다.
이를 원문제 혹은 Primal Problem이라 한다.

minimizexmaximizeμ≥0L(x,μ)\displaystyle \text{minimize}_{\textbf{x}} \text{maximize}_{\mu \geq 0} L(\textbf{x}, \mu)

원문제 최적화는 결국 다음을 만족하는 임계점 x∗\textbf{x}^*를 구하는 문제이다.

  1. g(x)≤0g(\textbf{x}) \leq 0
    제약 조건 하에서 해당 점은 실현가능해야 한다.

  2. μ≥0\mu \geq 0
    패널티는 항상 제약 조건의 범위 바깥의 값을 키우고, 안의 값에 영향을 끼치지 않는 올바른 방향이어야 한다. 이를 쌍대 실현 가능성 혹은 dual feasibility라 한다.

  3. μg(x∗)\mu g(\textbf{x}^*) =0
    우리는 원문제가 미분가능하며 연속이기를 바란다. 이는 제약 조건의 경계에서 실현가능한 점이란 경계 위에서 g(x)=0g(\textbf{x}) =0이고, 경계 안이라 할 수 있는 g(x)≤0g(\textbf{x}) \leq 0에 대해서는 라그랑지안에서 f(x∗)f(\textbf{x}^*)만 남도록 해야한다. 이는 결국 μ=0\mu = 0이 될 것이다.

  4. ∇f(x∗)−μ∇g(x∗)=0\nabla f(\textbf{x}^*) - \mu \nabla g(\textbf{x}^*) = 0
    이는 앞서 등호 제약식의 조건과 동일하다. 즉, 우리는 ff와 gg의 등고선이 일치하는 지역이 최적해라는 것을 알고 있고, 이를 찾기 위해 등고선과 수직인 그래디언트가 일치해야 한다. 만약 비활성화된 제약 조건 아래라면, ∇f(x)=0\nabla f(\textbf{x}) = 0이면서 μ=0\mu = 0으로 만족하게 될 것이다.

2. KKT 조건

지금까지 우리는 등식과 부등식 제약 조건이 어떻게 해결될 수 있는지 살펴보았다. 이를 일반화하여 nn개의 부등식과 등식 제약 조건을 가진 최적화 문제에서도 결국 일반화할 수 있다. 공통적으로 사용될 노테이션은 다음과 같다.

maximizexf(x)subject to g(x)≤0h(x)=0\begin{aligned} \text{maximize}_{\textbf{x}} \quad \quad & f(\textbf{x})\\ \text{subject to } \quad \quad& g(\textbf{x}) \leq 0\\ \quad \quad & h(\textbf{x}) = 0 \end{aligned}

앞으로 gg의 요소는 부등식 제약조건이고, hh의 요소는 등식 제약조건이 된다. 그리고 이 상황에서 일반화된 등식 및 부등식 제약조건을 가지는 최적화 문제는 KKT 조건이라 알려진 다음 네가지 조건을 만족해야한다.

  1. 실현가능성(feasibility) : 제약조건들을 모두 다음을 만족한다.

    g(x∗)≤0h(x∗)=0\begin{aligned} g(\textbf{x}^*) \leq 0\\ h(\textbf{x}^*) = 0 \end{aligned}

  2. 쌍대 실현 가능성(dual feasibilty) : 패널티는 실현가능한 영역으로 인도한다.

    μ≥0\mu \geq 0

  3. 상보 여유(complementary slackness) : 라그랑주 승수는 여유변수(slack)를 채우게 된다. 즉, 항상 μi=0\mu_i =0이거나 gi(x)=0g_i(\textbf{x}) = 0이다.

    μ⊙g=0\mu \odot g = 0

  4. 정상성(stationarity) : 목적함수의 등고선은 각 활성화된 제약과 접한다. 즉, 목적함수의 그래디언트는 각 활성화된 제약의 그래디언트와 동일하다.

    ∇f(x∗)=∑iμi∇gi(x∗)−∑jλi∇hj(x∗)=0\nabla f(\textbf{x}^*) = \sum_i \mu_i \nabla g_i(\textbf{x}^*) - \sum_j \lambda_i \nabla h_j(\textbf{x}^*) =0

위에서 이야기한 네가지 조건, 즉, KKT 조건은 모두 그래디언트와 관련된 1계 필요조건으로 평활한 제약조건을 가진 최적화 문제에서의 1계 필요조건이다.

3. 쌍대성(Duality)

이전에 정의한 라그랑지안에서 KKT 조건을 구하면서 이미 우리는 보다 일반화된 라그랑지안으로 확장할 수 있게 되었다. 해당 식은 다음과 같다.(이전의 라그랑지안과 다르게 λ\lambda의 부호가 바뀐 이유는 λ\lambda는 부호에 제약이 없기 때문에 보기 좋게 만든 것이다.)

L(x,μ,λ)=f(x)+∑iμigi(x)+∑jλjhj(x)L(\textbf{x}, \mu, \lambda) = f(\textbf{x}) + \sum_i \mu_i g_i(\textbf{x}) + \sum_j \lambda_j h_j(\textbf{x})

(위 식의 x,μ,λx, \mu, \lambda 모두 벡터임을 명심하자.)

여기서 원문제(primal problem)는 이전에도 이야기했듯이 위의 식을 이용해 본래의 최적화 문제로 다음과 같다.

primal form

minimizexmaximizeμ≥0,λL(x,μ,λ)\text{minimize}_{\textbf{x}} \text{maximize}_{\mu \geq 0, \lambda} L(\textbf{x}, \mu, \lambda)

하지만 원문제는 원래의 문제를 최적해를 구할 수 있도록 바꾼 것에 불과하므로, 여전히 최적해를 찾는 것이 쉽지는 않다. 이때문에, 최소화와 최대화의 순서를 바꾸어 최적화의 쌍대형태(dual form)를 만든다.

dual form

maximizeμ≥0,λminimizexL(x,μ,λ)\text{maximize}_{\mu \geq 0, \lambda} \text{minimize}_{\textbf{x}} L(\textbf{x}, \mu, \lambda)

그런데 이때 두 순서를 바꾸면 관계가 어떻게 되는지가 중요할 것이다. 이에 대한 max-min inequality는 다음과 같다.

max-min inequality

maximiazeaminimizebf(a,b)≤minimizebmaximiazeaf(a,b)\text{maximiaze}_a \text{minimize}_b f(\textbf{a}, \textbf{b}) \leq \text{minimize}_b \text{maximiaze}_a f(\textbf{a}, \textbf{b})

증명해보자
증명
어떤 함수 f(x,λ)f(\textbf{x}, \lambda)가 있다고 하자. 이때, λ\lambda를 고정하고 ff를 \textfx\textf{x}에 대해 최적화하면 아래와 같은 λ\lambda에 대한 식이 나올 것이다.

p(λ)=minxf(x,λ)p(\lambda) = min_{\textbf{x}} f(\textbf{x}, \lambda)

이때 p(λ)p(\lambda)는 당연하게도 어떠한 xx에 대해서도 ff의 가장 작은 값을 가지게 되므로 다음과 같은 부등식이 성립한다.

f(x,λ)≥p(λ)(1)f(\textbf{x}, \lambda) \geq p(\lambda) \tag{1}

이제 반대로 λ\lambda를 고정하여 x\textbf{x}에 대한 ff를 구해보자.

q(x)=maxλf(x,λ)(2)q(\textbf{x}) = max_\lambda f(\textbf{x}, \lambda) \tag{2}

이제 1의 식에 2의 식을 대입하면 다음과 같다.

q(x)=maxλf(X,λ)≥maxλp(λ)q(\textbf{x}) = max_\lambda f(\textbf{X}, \lambda) \geq max_\lambda p(\lambda)

이때 좌항은 x\textbf{x} 항 하나만 존재하는 식이지만, 우항은 상수임을 명심하자.

이때 모든 x\textbf{x}에 대해 위 부등식이 성립하기 때문에, 좌항을 최소화하여도 식이 성립할 것이다.

minxq(x)≥maxλp(λ)min_\textbf{x} q(\textbf{x}) \geq max_\lambda p(\lambda)

이제 식을 풀어보면 다음과 같이 min-max ineqaulity가 나오게 된다.

minxmaxλf(x,λ)≥maxλminxf(x,λ)min_\textbf{x} max_\lambda f(\textbf{x}, \lambda) \geq max_\lambda min_\textbf{x} f(\textbf{x}, \lambda)

다시 dual form과 primal form으로 돌아가보자.

primal formminimizexmaximizeμ≥0,λL(x,μ,λ)dual formmaximizeμ≥0,λminimizexL(x,μ,λ)\begin{aligned} &\text{primal form}\\ &\text{minimize}_{\textbf{x}} \text{maximize}_{\mu \geq 0, \lambda} L(\textbf{x}, \mu, \lambda)\\ \\ &\text{dual form}\\ &\text{maximize}_{\mu \geq 0, \lambda} \text{minimize}_{\textbf{x}} L(\textbf{x}, \mu, \lambda) \end{aligned}

두 식을 min-max inequality에 대입하면 primal form≥dual form\text{primal form} \geq \text{dual form}이므로 쌍대 문제의 해가 원문제 해의 하계를 이루고 있음을 알 수 있다.

이를 앞으로 d∗≤p∗d^* \leq p^*로 표기하자. 이때, d∗d^*는 쌍대값이고, p∗p^*는 원값이다. 또한 표기의 편의를 위해 쌍대 함수가 최대화 하는 내부의 함수를 쌍대 함수로 표기한다.

D(μ≥0,λ)=minimizexL(x,μ,λ)D(\mu \geq 0, \lambda) = \text{minimize}_\textbf{x} L(\textbf{x}, \mu, \lambda)

여기서 중요한 점은 쌍대 함수는 concave하다. concave 함수에서 그래디언트를 이용하면 항상 global maximum에 도달할 수 있다. 이를 이용해 x\textbf{x}에 대한 라그랑지안 최소화가 가능하다면, 즉, 쌍대 함수의 최소화가 용이하다면, 쌍대문제는 쉽게 최적화할 수 있다.

다시한번 짚고 넘어가자면, 쌍대 함수는 원문제의 하계를 이루고 있기 때문에 maximizeμ≥0,λD(μ,λ)≤p∗\text{maximize}_{\mu \geq 0, \lambda} D(\mu, \lambda) \leq p^*이다. 이는, 모든 μ≥0,λ\mu \geq0, \lambda에 대해 다음 식이 성립함을 의미하는 것이다.

D(μ≥0,λ)≤p∗D(\mu \geq 0, \lambda) \leq p^*

이때, 쌍대값과 원값의 차이(p∗−d∗p^* - d^*)이 존재하는데 이를 쌍대성 갭(duality gap)이라 부른다.

쌍대성의 좋은 점은 특별한 경우에 원문제와 쌍대성 문제가 같은 해를 같는 것이 보장되어, 쌍대성 갭이 0이고, 원문제를 푸는 대신에 쌍대성 문제를 풀어 해를 구할 수 있다는 점이다.

참고

일리노이 공대 vista 연구실의 쌍대성에 관한 자료

profile
김재희
이전 포스트

9. 등식 제약조건

0개의 댓글