크루스칼 - 원더랜드(최소스패닝트리 : 크루스칼, Union&Find 활용)

문제

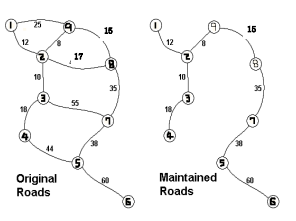
원더랜드에 문제가 생겼다. 원더랜드의 각 도로를 유지보수하는 재정이 바닥난 것이다.
원더랜드는 모든 도시를 서로 연결하면서 최소의 유지비용이 들도록 도로를 선택하고 나머지 도로는 폐쇄하려고 한다. 도로를 공사하여 길을 최소비용으로 짓는 비용을 구하여라.

입력
9 12
1 2 12
1 9 25
2 3 10
2 8 17
2 9 8
3 4 18
3 7 55
4 5 44
5 6 60
5 7 38
7 8 35
8 9 15

출력 
196

풀이

class Load implements Comparable<Load>{
    int a;
    int b;
    int c;
    public Load(int a, int b, int c) {
        this.a = a;
        this.b = b;
        this.c = c;
    }
    @Override
    public int compareTo(Load o) {
        return this.c - o.c;
    }
}
public class ex7 {
    static int v,e;
    static int[] unf;
    static ArrayList<Load> graph;

    public static int Find(int v){
        if(unf[v]==v) return v;
        else return unf[v]=Find(unf[v]);
    }
    public static void Union(int a, int b){
        int fa = Find(a);
        int fb = Find(b);
        if(fa != fb) unf[fa] = fb;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        v = sc.nextInt();
        e = sc.nextInt();
        graph = new ArrayList<>();
        unf = new int[v+1];
        for(int i=1; i<=v; i++) unf[i]=i;

        for(int i=0; i<e; i++){
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            graph.add(new Load(a,b,c));
        }

        int answer=0;
        Collections.sort(graph);
        for(Load x : graph){
            int fa = Find(x.a);
            int fb = Find(x.b);
            if(fa!=fb){
                answer+=x.c;
                Union(x.a,x.b);
            }
        }

        System.out.println(answer);
    }
}

1. 객체를 하나 만들어서 정점 a->b, 비용 c 를 담는다. 그리고 graph라는 리스트에 각 입력정보를 담고 비용이 낮은 순으로 정렬한다.

2. 문제에서 요구하는 것은 도로가 서로 순회하지 않고 트리구조가 되는 것을 원하기 때문에 Union&Find 방식(=서로소집합 : 공통원소 x)을 사용한다.

3. 간단하다. graph의 낮은 비용순으로 forEach해서 Find()한 a,b의 두 결과 fa,fb가 일치하지 않으면 이 둘은 집합이 아니기 때문에 Union()을 이용해 집합으로 만들어주고 , answer에 비용을 담는다.