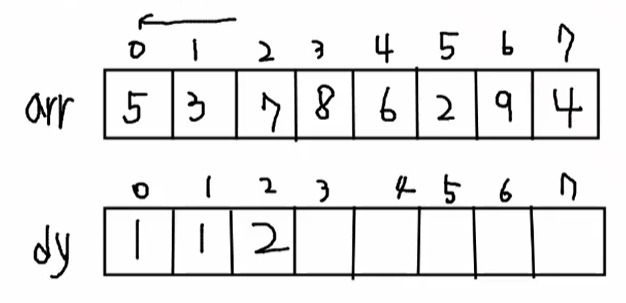
1. 최대부분 증가수열
N개의 자연수로 이루어진 수열이 주어졌을 때, 그 중에서 가장 길게 증가하는(작은 수에서 큰
수로) 원소들의 집합을 찾는 프로그램을 작성하라.
//입력
8
5 3 7 8 6 2 9 4
//출력
4
풀이
public class ex3 {
static int n;
static int[] arr;
static int[] dy;
public static int solution(){
int answer=0;
dy[0]=1;
for(int i=0; i<n; i++){
int max=0;
for(int j=i-1; j>=0; j--){
if(arr[j]<arr[i] && dy[j]>max) max=dy[j];
}
dy[i]=max + 1;
answer = Math.max(answer,dy[i]);
}
return answer;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
arr = new int[n];
dy = new int[n];
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
}
System.out.println(solution());
}
}
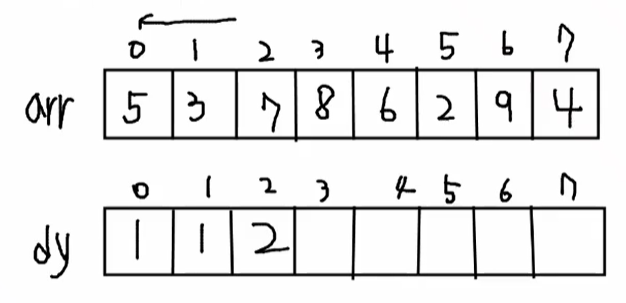
- 각각의 경우에서의 최댓값을 저장할 dy[]를 생성한다.
- arr을 입력받고 2중 for문으로 j=i-1로 가면서 해당 i의 경우에서의 최댓값을 구하는 for문을 돌린다.
- 그 중에서의 최대값을 구해서 answer 리턴.
2. LIS 활용 - 가장 높은 탑 쌓기
밑면이 정사각형인 직육면체 벽돌들을 사용하여 탑을 쌓고자 한다. 탑은 벽돌을 한 개씩 아래
에서 위로 쌓으면서 만들어 간다. 아래의 조건을 만족하면서 가장 높은 탑을 쌓을 수 있는 프
로그램을 작성하시오.
(조건1) 벽돌은 회전시킬 수 없다. 즉, 옆면을 밑면으로 사용할 수 없다.
(조건2) 밑면의 넓이가 같은 벽돌은 없으며, 또한 무게가 같은 벽돌도 없다.
(조건3) 벽돌들의 높이는 같을 수도 있다.
(조건4) 탑을 쌓을 때 밑면이 좁은 벽돌 위에 밑면이 넓은 벽돌은 놓을 수 없다.
(조건5) 무게가 무거운 벽돌을 무게가 가벼운 벽돌 위에 놓을 수 없다.
//입력
5
25 3 4 --> 밑면넓이 , 높이 , 무게
4 4 6
9 2 3
16 2 5
1 5 2
//출력
10
풀이
class Doll implements Comparable<Doll>{
int s;
int h;
int w;
public Doll(int s, int h, int w) {
this.s = s;
this.h = h;
this.w = w;
}
@Override
public int compareTo(Doll o) {
return o.s - this.s;
}
}
public class ex4 {
static int n;
static ArrayList<Doll> arr;
static int[] dy;
public static int solution(){
int answer=0;
Collections.sort(arr);
dy[0] = arr.get(0).h;
for(int i=0; i<n; i++){
int max_h=0;
for(int j=i-1; j>=0; j--){
if(arr.get(j).w > arr.get(i).w && dy[j] > max_h) max_h=dy[j];
}
dy[i]=max_h + arr.get(i).h;
answer = Math.max(answer,dy[i]);
}
return answer;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
dy = new int[n];
arr = new ArrayList<>();
for(int i=0; i<n; i++){
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
arr.add(new Doll(a,b,c));
}
System.out.println(solution());
}
}
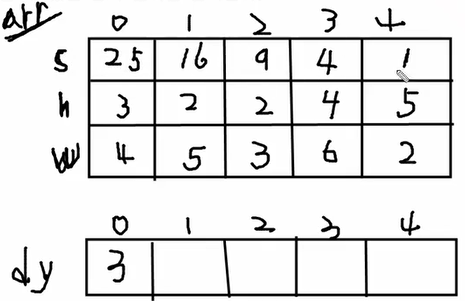
- 위 그림과 같이 s,h,w를 담는 Doll객체를 만들어준다. 그리고 입력을 담는다.
- Doll객체를 밑면의 넓이 순으로 정렬한다.
- 2중 for문을 이용해 순차적으로 각 돌의 위치에서의 최대높이를 측정한다. 이때 arr.get(j).w 가 arr.get(i).w 보다 무거워야 한다.