곱셈 암호(Multiplicative Ciphers)
- 암호 알고리즘: 평문에 키를 곱하여 암호 -> C = (P x K) mod 26
- 복호 알고리즘: 암호문에 키의 역원을 곱하여 복호화 -> P = (C x k^-1) mod 26
주의!
암호/복호화 시 모든 연산은 Z26*(Z26의 원소 중 곱셈에 대한 역원을 갖는 원소들만 모아놓은 것, 곱셈 암호에서의 키 공간)에서 모듈러 연산(mod 26)수행
- 복호화를 위해 키를 나누는 과정은 Z26에서 해당 키의 곱셈에 대한 역원(k^-1)을 곱하는 과정
- 복호화를 위해 곱셈에 대한 역원이 존재해야 하므로, Z6이 아닌 Z26*를 키 집합을 사용
- 평문, 암호문의 각 글자 ∈ Z26
- 키 값 ∈ Z26*
- 모듈러 곱셈의 역원이 존재하지 않는 경우가 존재함 -> 이 key를 사용하면 복호화가 불가능함
- 최소잉여집합 아래 최종 연산 => 모듈러 연산
곱셈 암호의 기본 개념

- 송신자, 수신자 같은 키를 사용함 -> 대칭키 암호
- cf) 비대칭키 암호
- 암호화 키 공개 (일반적인 비대칭키 암호)
- 복호화 키 공개: 암호화를 나만 알 수 있는 것 (전자서명, 공인인증서)
예제1) 26개의 알파벳에 대응되는 Z26에서 곱셈 암호에 대한 키 공간은?
- 덧셈에 대한 역원: Z26 = {0,1,2,, ..., 25}
- Z26에 속하는 모든 원소들은 덧셈에 대한 역원을 가짐
- 그러나 모든 원소들이 곱셈에 대한 역원을 가지지는 않은ㅁ
- 곱셈에 대한 역원: Z26 = {1,3,5,7,9,11,15,17,19,21,23,25} ⊂ Z26
- Z26에서 곱셈에 대한 역원을 갖는 원소들로 구성된 Z26의 부분집합임
예제2) key = 7일 때, 평문 "hello"를 암호화하시오.

h: 7 -> (7x7) mod 26 = 23 -> X
e: 4 -> (4x7) mod 26 = 2 -> C
l: 11 -> (11x7) mod 26 = 25 -> Z
l: 11 -> (11x7) mod 26 = 25 -> Z
o: 14 -> (14x7) mod 26 = 20 -> U
예제3) key = 7일 때, 암호문 "XCZZU"를 복호화하시오.
- Z26에서 7의 역원 (7^-1)은 15이다.
X: 23 -> (23x7^-1) mod 26 = 7 -> h
C: 2 -> (2x7^1) mod 26 = 4 -> e
Z: 25 -> (25x7^1) mod 26 = 11 -> l
Z: 25 -> (25x7^1) mod 26 = 11 -> l
U: 20 -> (20x7^1) mod 26 = 14 -> o
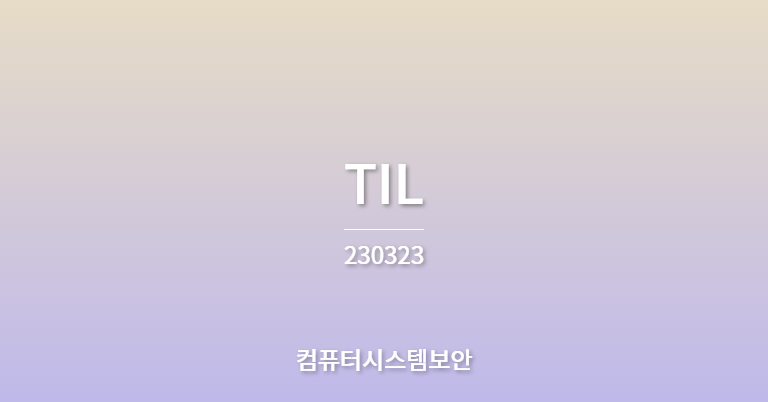
아핀 암호(Affine Cipher)
덧셈.곱셈 암호는 키 공간이 작기 때문에 보안에 취약함
key 2개를 사용하는 아핀 암호 등장
- 암호 알고리즘 -> C = (p x k1 + k2) mod 26
- 복호 알고리즘 -> P = ((C - k2) x k1^-1) mod 26
- k1^-1은 k1의 곱셈에 대한 역원이고, -k2는 k2의 덧셈에 대한 역원
암호화: x -> +
복호화: +역원 -> x역원
복화화는 암호화의 역원이기 때문에 연산 순서도 반대가 됨
예제1) 키 쌍이 (7,2)인 아핀 암호를 사용해 평문 "hello"를 암호화하시오
- 키 쌍이 (7,2) -> 곱셈 암호에 대한 키 k1 - 7, 덧셈 암호에 대한 k2 = 2
- 암호화 공식 C = (P x k1 + k2) mod 26 이용
h: 7 -> (7x7+2) mod 26 = 25 -> Z
e: 4 -> (4x7+2) mod 26 = 4 -> E
l: 11 -> (11x7+2) mod 26 = 1 -> B
l: 11 -> (11x7+2) mod 26 = 1 -> B
o: 14 -> (14x7+2) mod 26 = 22 -> W
예제 2) 키 쌍이 (7,2)인 아핀 암호를 사용해 암로문 "ZEBBW"를 복호화하시오
- 키 쌍이 (7,2) -> 곱셈 암호에 대한 키 k1 - 7, 덧셈 암호에 대한 k2 = 2
- 복호화 공식 P = ((C - k2) x k1^-1) mod 26 이용
- k1 = 7, Z26에서 역원은 15임
Z: 25 -> ((25-2)x7^-1) mod 26 = 7 -> h
E: 4 -> ((4-2)x7^-1) mod 26 = 4 -> e
B: 1 -> ((1-2)x7^-1)mod 26 = 11 -> l
B: 1 -> ((1-2)x7^-1)mod 26 = 11 -> l
W: 22 -> ((22-2)x7^-1)mod 26 = 14 -> o
다중문자 암호
- 다중문자 대치(Polyalphabetic subtitution)에서는 각 문자가 다른 대치를 가짐
- 평문 문자와 암호문 문자와의 관계 - > 일대다 대응 관계
- 단일 문자 암호체계와 비교했을 때, 대비 단어 빈도 수 분석을 통한 암호문 해독이 더욱 어려운 장점이 있음
- 다중 문자 암호를 구성하기 위해 메시지에서 평문 문자와 그 문자의 위치에 따라 암호문 문자를 생성함
- 즉, 다중 문자 암호체계에서 사용되는 키 = 암호화 할 때 평문 문자의 위치에 따라 정해지는 부분키들로 구성된 키 수열
자동키 암호(Autokey cipher)
- 키: 여러 개의 부분 키들로 구성된 수열
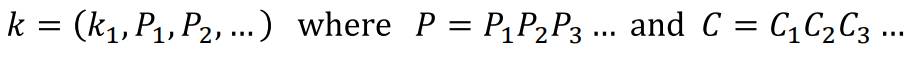
- 각 부분키는 평문에서 대응되는 문자를 암호화하는 데 사용
- 첫 번째 부분키: 송신자와 수신자가 비밀리에 합의한 사전에 정의된 값
- 두 번재 부분키: 첫 번째 평문 문자 값
- 세 번째 부분키: 두 번째 평문 문자 값
- "자동키" 명칭의 유래: 암호화 과정 중 부분키가 평문으로부터 자동으로 생성됨을 의미함
- 평문의 종류에 따라 전체적인 key값이 달라짐
자동키 암호의 암호화/복호화 원리
- 암호화: Ci = (Pi + ki) mod 26
- 복호화: Pi = (Ci - ki) mod 26
- 키: k = (k1, P1, P2, ...)
자동키 암호 예제)
- 송신자와 수신자가 초기 키 값을 12로 가진 자동키 암호를 사용한다고 가정하자. 이때, 송신자가 수신자에게 "attack is today"라는 메시지를 보내려고 한다. 이를 암호화하여라.