Brute Force
- 문제의 진술과 관련 개념에 대한 정의를 바탕으로 문제를 해결하기 위한 간단한 접근법
- 억지 기법(무차별 대입해 억지로 문제를 푸는)
Sort
Bubble Sort(버블 정렬): O(n^2)

Selection Sort(선택 정렬): O(n^2)

Sequential Search(순차 탐색): O(n)

Striig Matching

비교
The worst case: Θ(n * m)
A average natural language text: Θ(n+m) = Θ(n)
Closet Pair Problem
- k차원 공간에서 n개의 점 집합에서 가장 가까운 두 점 찾기
Euclidean distance

Convex Hull Problem
- Convex set: 집합 내의 임의의 두 점 P와 Q에 대해, 끝점이 Q 및 Q인 전체 선분 세트에 속함
- Convex hull(볼록 껍질): 점들의 집합 S의 볼록 껍질은 S를 포함하는 가장 작은 볼록 집합임
- "가장 작은" 요건은 S의 볼록 껍질이 S를 포함하는 볼록 집합의 부분 집합이어야 한다는 것을 의미함
- n>2인 점의 임의의 집합 S의 볼록 껍질은 S의 점 중 일부에 꼭짓점이 있는 볼록 다각형임
- 볼록 집합의 극한점은 집합에 끝점이 있는 선분의 중간점이 아닌 이 집합의 점임
알고리즘
- n(n-1)/2 쌍의 구별되는 점 각각에 대해 점1 = (x1, y1), 점2 = (x2, y2)
- a = y2 - y1, b = x2 - x1, c = x1y2 - y1x2일 때, ax + by = c의 직선을 구함
- 각각의 다른 n-2 포인트에 대해 ax + c를 구함
- 모든 점이 같은 부호를 갖는 경우 두 점은 극장점 중 하나임
- 이 알고리즘의 시간 효율: O(n^3)
Exhaustive Search(완전 탐색)
- State-space search
- 초기 상태, 목표 상태, 작업 집합에서 초기 상태를 목표 상태로 변환하는 일련의 작업을 찾음
- 솔루션 과정을 트리로 나타낼 수 있음
조합 문제
- Traveling Salesman - permutations(순열) Θ((n-1)!): 순회판매원 문제
- Knapsack - subset(부분 집합) Θ(n!): 배낭 문제
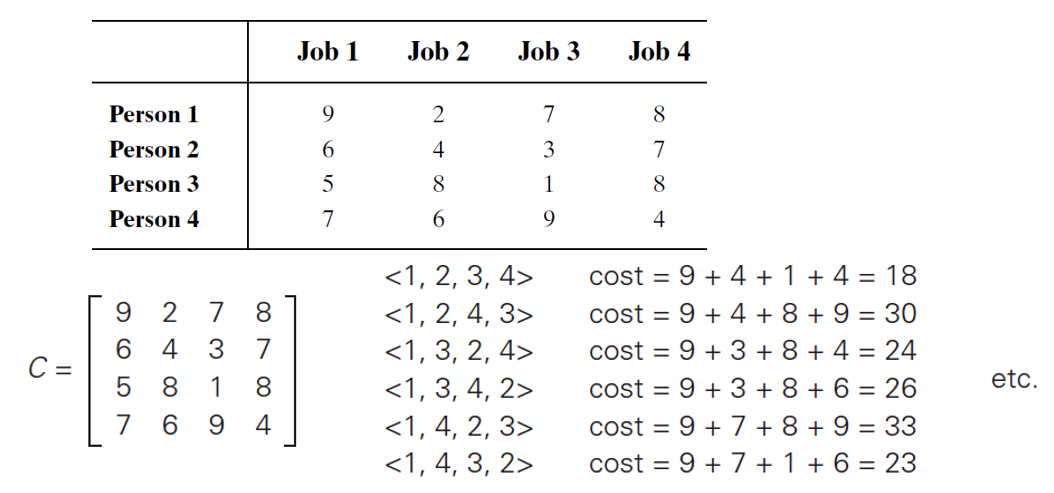
- Assignment problem(할당 문제) - permutations(순열) Θ(n!)
1. TSP(Traveling Salesman Problem)
- 주어진 n개 도시를 통과하는 최단 투어를 찾음
- 출발지 도시로 돌아가기 전에 각 도시를 정확히 한 번 방문
- 도시를 나타내는 그래프의 정점과 거리를 지정하는 가장자리 가중치를 사용하여 가중치 그래프로 편리하게 모델링
- 그래프에서 가장 짧은 해필턴 회로를 찾는 것과 같음
- 해밀턴 회로는 그래프의 모든 꼭짓점을 정확히 한 번 동과하는 주기(cycle)로 정의됨

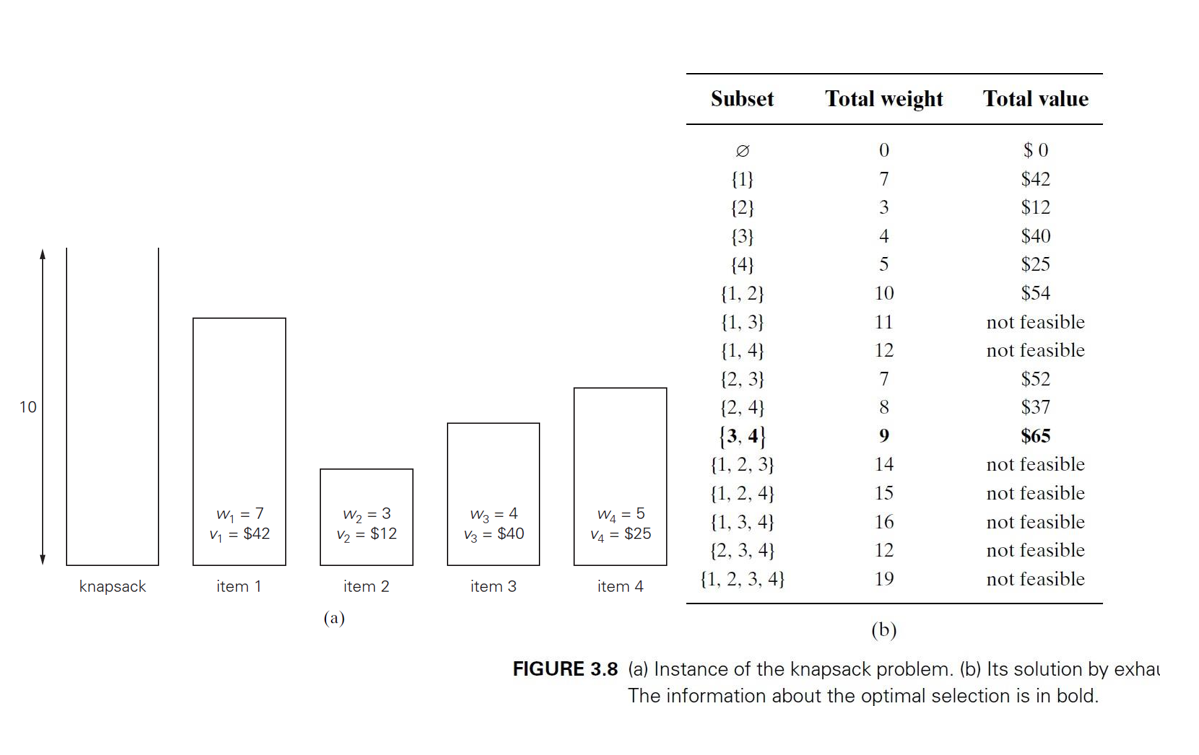
2. Knapsack Problem
- 알려진 가중치 w1, w2, ..., wn 및 값 v1, v2, ..., vn 및 용량의 배낭의 n개 항목이 주어짐
- 0/1 knapsack problem과 TSP는 NP-난해 문제
3. Assignment Problem
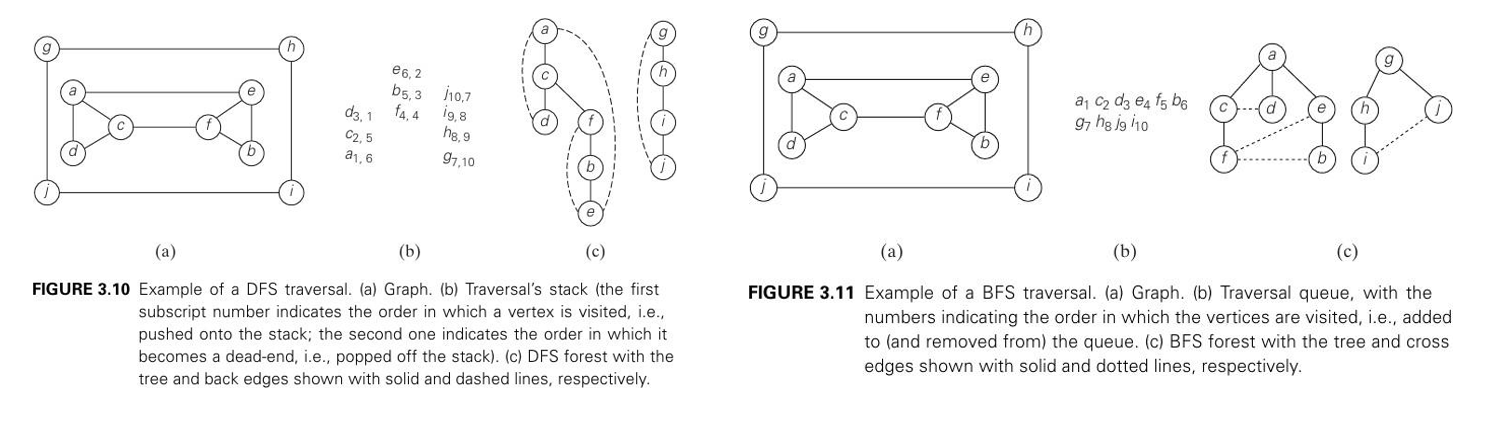
DFS and BFS
- Depth First Search
- Breadth First Search
결론
강점
- 광범위한 적용성, 단순성
- 검색, 문자열 일치 및 행렬 곱셈과 같은 몇 가지 중요한 문제에 대한 합리적인 알고리즘
- n개의 숫자와 합과 곱, 목록에서 최대값 또는 최소값 찾기와 같은 간단한 계산 작업을 위한 표준 알고리즘
약점
- Brute Force 접근 방식은 효율적인 알고리즘을 산출하는 경우가 거의 없음
- 일부 무차별 힘 알고리즘은 허용할 수 없을 정도로 느림
- Brute Force 접근 방식은 다른 설계 기법만큼 건설적이지도 않고 창의적이지도 않음

