입력 크기 측정
- 시간 효율 : 입력 크기의 함수로서 기본 연산의 반복 횟수
- 입력 크기는 다음의 영향을 받음
- 행렬과 같은 데이터 표현
- 예를 들어 철자 맞추기와 같은 알고리즘의 연산
- 예를 들어 주어진 정수가 소수인지 확인하는 등 문제의 객체 속성
알고리즘에 사용하는 자료형에 영향을 받음
- 배열에서 x 찾기: 배열에 있는 요소 수
- 두 행렬을 곱함: 행렬의 차원
- 배열 정렬: 배열의 요소 수
- 이진 트리 탐색: 노드 수
- 선형 방정식 시스템: 방정식의 수 또는 알 수 없는 수 또는 둘 다
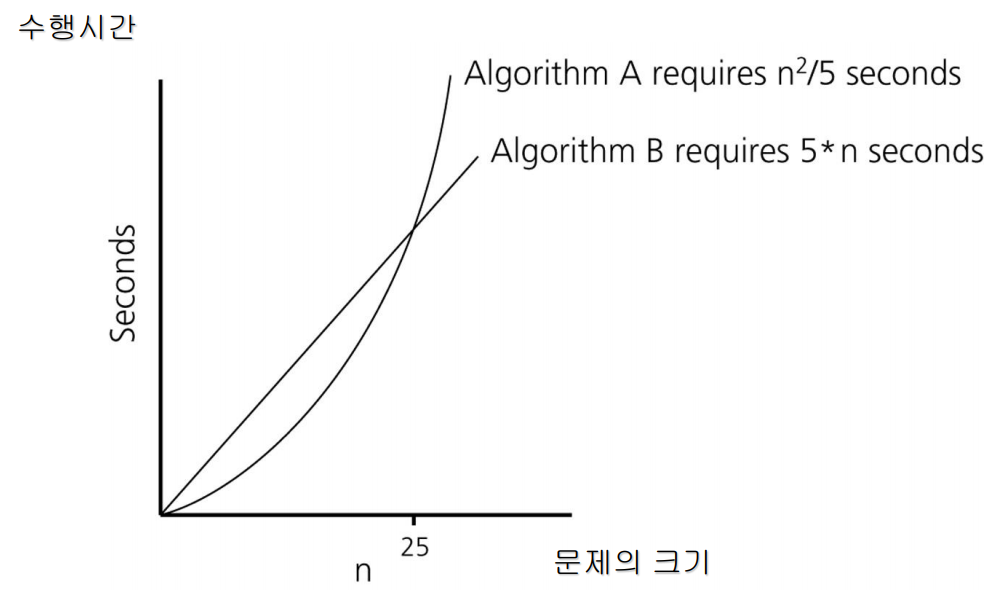
실행 시간 측정 단위
- 표준 시간 단위를 사용하는 것은 적절하지 않음
- 알고리즘에서 모든 작업을 계산하는 것은 적절하지 않음
- 접근 방식: 알고리즘의 기본 작업 식별 및 카운트
- 기본 작업
- 알고리즘을 수행하기 위해 모든 입력 항목에 적용됨
- 알고리즘의 실행 시간에 가장 많이 기여
- 배열에서 x 찾기: 배열의 항목과 x의 비교
- 두 행렬에 실제 항목을 곱하는 방법: 두 실수의 곱셈
- 숫자 배열 정렬: 두 배열 항목과 배열의 이동 요소 비교
- 트리 탐색: 모서리(edge) 탐색
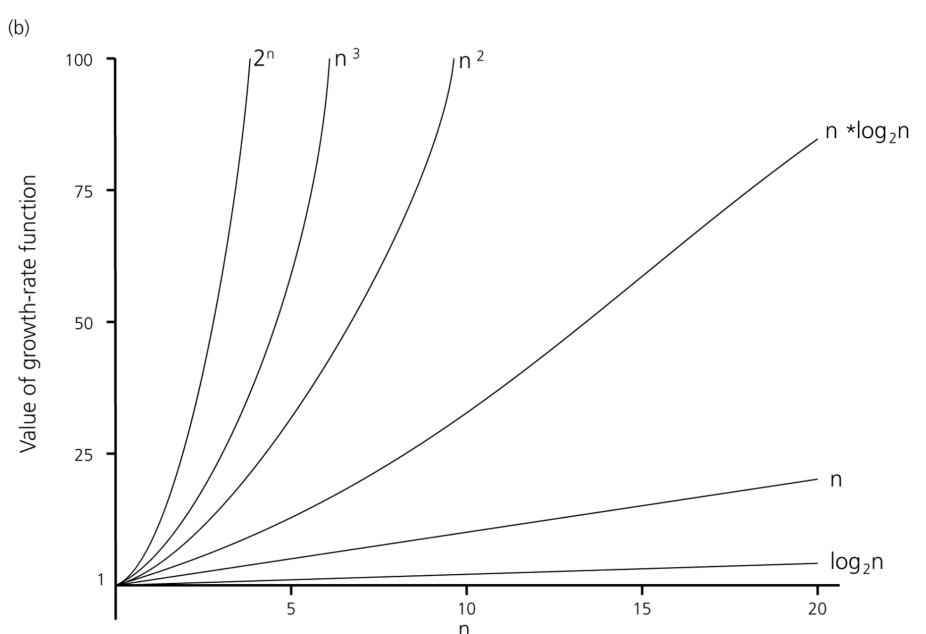
Growth of functions
점근 표기법
- O-표기호
- Ω 표기법
- θ-표기
- 기타 유형의 표기법
- 한계 내 함수의 동작을 설명하는 방법 -> 점근 효율
- 중요한 것에 집중하라
- 낮은 차수의 항과 상수 인자를 추상화하여 제거
- 알고리즘의 실행 시간을 어떻게 표시합니까?
- 함수의 "크기"를 비교하는 방법
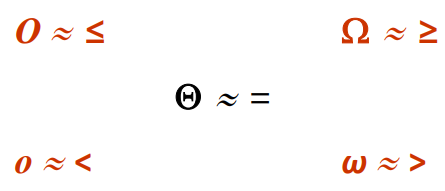
유추
- f(n) = O(g(n)) ≈ f(n) ≤ g(n) in degree.
- f(n) = Ω(g(n)) ≈ f(n) ≥ g(n) in degree.
- f(n) = Θ(g(n)) ≈ f(n) = g(n) in degree.
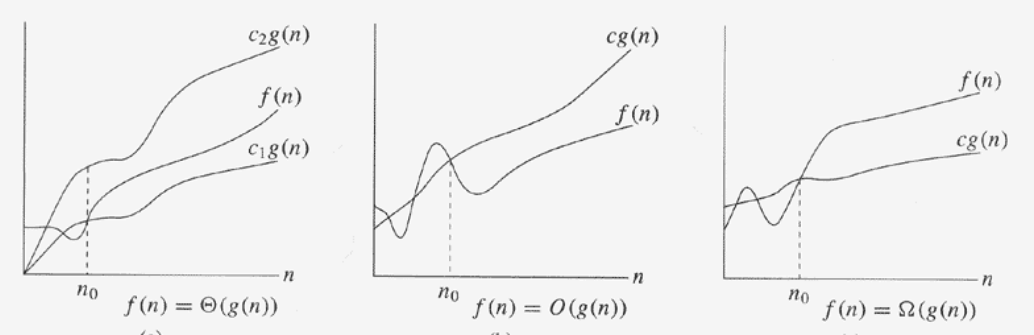
O 표기법 -> 상한

중간값 != 평균
O(NlgN) vs O(N)
Ω 표기법 -> 하한

값을 줄일 때
: 루트보단 로그 사용
Θ 표기법 -> 점근적으로 근접한 한계값

f (n) = Θ (g(n)) iff f = O (g(n)) and f = Ω (g(n)).
점근 표기법
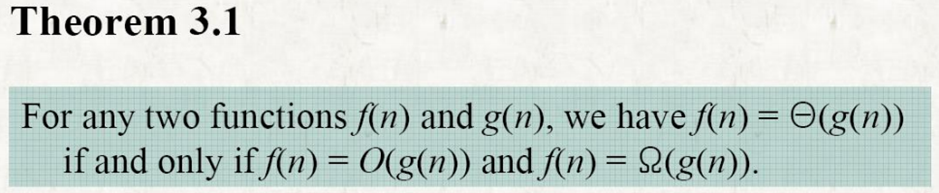
-
방정식 및 부등식 표기법
-
n = O(n2) (set)
-
T(n) = 2T(n/2) + Θ(n) (element)
-
2n^2 + Θ(n) = Θ(n^2)
- f(n) = Θ(g(n)) ≈ f(n) = g(n) in degree.
- f(n) = O(g(n)) ≈ f(n) ≤ g(n) in degree.
- f(n) = Ω(g(n)) ≈ f(n) ≥ g(n) in degree.
- f(n) = o(g(n)) ≈ f(n) < g(n) in degree.
- f(n) = ω(g(n)) ≈ f(n) > g(n) in degree.
함수 비교
- Transitivity:전이성 ( =, ≤, ≥, <, > )
- Reflexivity:반사율 ( =, ≤, ≥ )
- Symmetry:대칭 ( = )
- Transpose symmetry:전치 대칭 ( ≤ ↔ ≥, < ↔ > )
Transitivity ( =, ≤, ≥, <, > )
- f(n) = Θ(g(n)) and g(n) = Θ(h(n)) imply f(n) = Θ(h(n)),
- f(n) = O(g(n)) and g(n) = O(h(n)) imply f(n) = O(h(n)),
- f(n) = Ω(g(n)) and g(n) = Ω(h(n)) imply f(n) = Ω(h(n)),
- f(n) = o(g(n)) and g(n) = o(h(n)) imply f(n) = o(h(n)),
- f(n) = ω(g(n)) and g(n) = ω(h(n)) imply f(n) = ω(h(n))
Reflexivity ( =, ≤, ≥ )
- f(n) = Θ(f(n))
- f(n) = O(f(n))
- f(n) = Ω(f(n))
Symmetry ( = )
- f(n) = Θ(g(n)) if and only if g(n) = Θ(f(n)).
Transpose symmetry ( ≤ ↔ ≥, < ↔ > )
- f(n) = O(g(n)) if and only if g(n) = Ω(f(n)),
- f(n) = o(g(n)) if and only if g(n) = ω(f(n)).
비교
Related Properties:
- Transitivity:
f (n) = Θ(g(n)) and g(n) = Θ(h(n))⇒ f (n) = Θ(h(n))
Same for O, Ω, o, and ω - Reflexivity:
f (n) = Θ( f (n))
Same for O and Ω - Symmetry:
f (n) = Θ(g(n)) if and only if g(n) = Θ( f (n)) - Transpose symmetry:
f (n) = O(g(n)) if and only if g(n) = Ω( f (n))
f (n) = ω(g(n)) if and only if g(n) = ω( f (n))
Comparisons:
- f (n) is asymptotically smaller than g(n) if f (n) = o(g(n))
- f (n) is asymptotically larger than g(n) if f (n) = ω(g(n))

