백준 1463, 2839, 11057 (DP)

1463 : 1로 만들기

정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지이다.

• X가 3으로 나누어 떨어지면, 3으로 나눈다.
• X가 2로 나누어 떨어지면, 2로 나눈다.
• 1을 뺀다.

정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

입력

첫째 줄에 1보다 크거나 같고, $10^6$보다 작거나 같은 정수 N이 주어진다.

출력

첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.

풀이

예를 들어 입력값이 10이면 10 → 9 → 3 → 1, 연산 횟수의 최솟값인 3을 출력해야 한다. 해당 문제는 세가지 방법 모두 연산 횟수를 비교해 minimum 값을 뽑도록 구현해야 한다. 따라서 아래 코드 소스와 같이 세가지 연산을 모두 차례대로 비교하여 연산 횟수의 최솟값을 찾아내는 방식으로 구현하였다.

1. 1을 뺀다
   d[i] = d[i - 1] + 1
2. 만약 i가 2로 나눠지면, d[i]와 d[i//2]+1 중에 더 작은 값을 d[i]로 정의
   d[i] = min(d[i], d[i // 2] + 1)
   
3. 만약 i가 3으로 나눠지면, d[i]와 d[i//3]+1 중에 더 작은 값을 d[i]로 정의
   d[i] = min(d[i], d[i // 3] + 1)

처음에는 입력값부터 나눠야 한다고 생각하니까 방법이 잘 생각나지 않았는데, 반대로 작은 값부터 생각하니까 쉬운 접근이 가능했다.

코드

n = int(input())

d = [0] * (n + 1)

for i in range(2, n + 1):
    d[i] = d[i - 1] + 1
    if i % 2 == 0:
        d[i] = min(d[i], d[i // 2] + 1)
    if i % 3 == 0:
        d[i] = min(d[i], d[i // 3] + 1)

print(d[n])

# 다른 풀이

n = int(input()) + 1
d = [0] * n

for i in range(2,n):
  d[i] = min(d[i-1],d[i//3]+i%3,d[i//2]+i%2) + 1
  
print(d[-1])

2839 : 설탕 배달

상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그램 봉지와 5킬로그램 봉지가 있다.

상근이는 귀찮기 때문에, 최대한 적은 봉지를 들고 가려고 한다. 예를 들어, 18킬로그램 설탕을 배달해야 할 때, 3킬로그램 봉지 6개를 가져가도 되지만, 5킬로그램 3개와 3킬로그램 1개를 배달하면, 더 적은 개수의 봉지를 배달할 수 있다.

상근이가 설탕을 정확하게 N킬로그램 배달해야 할 때, 봉지 몇 개를 가져가면 되는지 그 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N이 주어진다. (3 ≤ N ≤ 5000)

출력

상근이가 배달하는 봉지의 최소 개수를 출력한다. 만약, 정확하게 N킬로그램을 만들 수 없다면 -1을 출력한다.

풀이

먼저 N이 가질 수 있는 최댓값은 5000이므로, DP 테이블은 5001이라는 값을 N + 1개 가진 리스트로 만든다. 여기서 5001은 정확하게 N킬로그램을 만들 수 없다는 의미이기도 하다.

상근이가 가져갈 수 있는 봉지의 무게는 3킬로그램 혹은 5킬로그램이다. 따라서 해당 봉지의 무게를 array라는 리스트로 정의해준다. 무게에 따른 봉지는 두 종류이고, 이에 따라 array에도 두개의 값만이 존재하므로 외부 for문은 두 번 반복되도록 range를 2로 해주었다. 내부 for문에서는 봉지의 무게에 따라 개수를 갱신하는 코드를 작성했다.

예를 들어, N이 11이라면 외부 for문이 처음 돌아갈 때, array[0] = 3이므로 내부 for문에선 다음과 같이 dp 테이블을 갱신한다.

• d[3] = min(d[3] = 5001, d[3-3] + 1 = 1) = 1
• d[4] = 5001
• d[5] = 5001
• d[6] = min(d[6] = 5001, d[6-3] + 1 = 2) = 2
• d[7] = 5001
• d[8] = 5001
• d[9] = min(d[9] = 5001, d[9-3] + 1 = 3) = 3
• d[10] = 5001
• d[11] = 5001

다음으로 외부 for문이 두 번째로 돌아갈 때는 array[1] = 5이므로 내부 for문에서 dp 테이블이 또 다시 갱신된다.

• d[5] = min(d[5] = 5001, d[5-5] + 1 = 1) = 1
• d[6] = min(d[6] = 2, d[6-5] + 1 = 5002) = 2
• d[7] = 5001
• d[8] = min(d[8] = 5001, d[8-5] + 1 = 2) = 2
• d[9] = 3
• d[10] = min(d[10] = 5001, d[10-5] + 1 = 2) = 2
• d[11] = min(d[11] = 5001, d[11-5] + 1 = 3) = 3

결론적으로 11킬로그램 설탕을 배달할 때의 최소 봉지 개수는 3개(3+3+5)이다.

마지막으로 d[n] = 5001이면 3과 5의 합으로 n을 만들 수 없다는 의미이므로, 문제의 요구와 같이 -1을 출력하도록 if문을 작성하였다.

코드

n = int(input())

d = [5001] * (n + 1)
array = [3, 5]

d[0] = 0
for i in range(2):
  for j in range(array[i], n + 1):
    d[j] = min(d[j], d[j - array[i]] + 1)

if d[n] == 5001:
  print(-1)
else:
  print(d[n])

11057: 오르막 수

오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.
예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.
수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.

입력

첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.

출력

첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.

풀이

비교적 오래 고민했지만 답은 생각보다 간단했던.. 규칙을 찾기만 하면 쉽게 풀리는 문제였다.

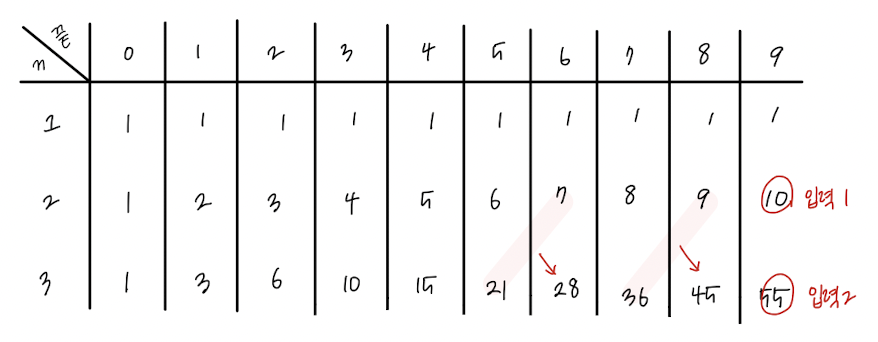
오르막 수는 문제에서 언급한 것과 같이 수의 자리가 오름차순을 이루는 수이다. 예를 들어 끝자리 수가 2이고 N이 3일 때는 002, 012, 022, 112, 122, 222 총 여섯가지의 오르막 수가 존재한다.

위와 같이 끝자리 수와 수의 길이 N에 따른 표를 그려보니 d[j] += d[j-1] 의 방식으로 dp 테이블을 갱신하면 되는 문제라는 것을 알 수 있었다.

: $DP[i][j]=∑_{k=0}^{j}DP[i−1][k]$로부터 도출

따라서 처음 dp 테이블은 초깃값(N=1)인 1을 10개 가진 리스트로 정의하고, d[j] += d[j-1] 방식으로 테이블을 갱신하도록 중첩 반복문을 작성하였다.

코드

n = int(input())

d= [1] * 10

for i in range(n - 1):
  for j in range(1, 10):
    d[j] += d[j - 1]

print(sum(d) % 10007)