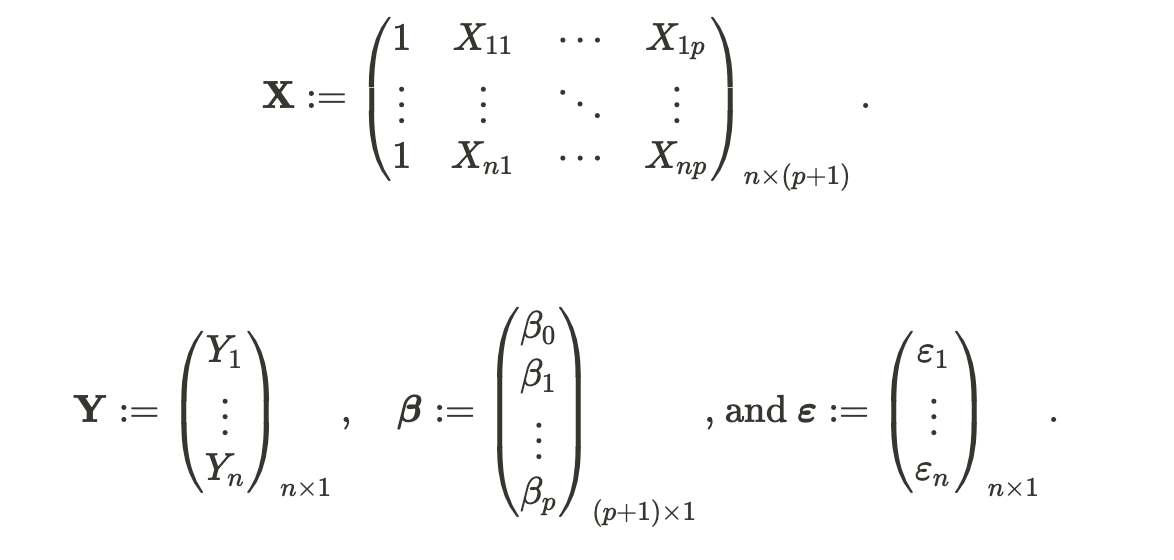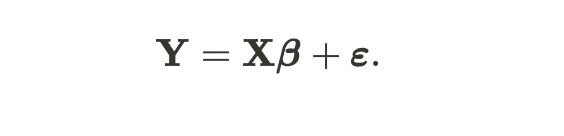Linear Regression
Simple linear model
y = β 0 + β 1 X + ϵ y = \beta_0 + \beta_1X + \epsilon y = β 0 + β 1 X + ϵ
Simple linear 모델은 위의 식과 같은 선형 관계를 가정함으로써 만들어진다.
random variable ϵ \epsilon ϵ ϵ \epsilon ϵ
E [ Y ∣ X = x ] = β 0 + β 1 x , \ \mathbb{E}[Y|X=x] = \beta_0 + \beta_1x, E [ Y ∣ X = x ] = β 0 + β 1 x ,
s i n c e E [ ϵ ∣ X = x ] = 0 since\ \mathbb{E}[\epsilon|X=x]=0 s i n c e E [ ϵ ∣ X = x ] = 0
위 식의 좌변은 Y ∣ X Y|X Y ∣ X X X X Y Y Y
즉, 좌변과 우변을 통해 Y Y Y 의 평균이 X X X 는 것을 나타낸다.
β 0 \beta_0 β 0 Y Y Y X = 0 X = 0 X = 0 β 1 \beta_1 β 1 Y Y Y X = x X=x X = x
우리에게 sample이 있다면, uncertain coefficients인 β 0 , β 1 \beta_0, \beta_1 β 0 , β 1
estimate하는 방법은 certain optimality를 찾는 것
예를 들어 the minimization of the Residual Sum of Squares (RSS)를 통해
R S S ( β 0 , β 1 ) : = ∑ i = 1 n ( Y i − β 0 − β 1 X i ) 2 RSS(\beta_0, \ \beta_1) := \sum_{i=1}^{n}(Y_i -\beta_0 -\beta_1X_i)^2 R S S ( β 0 , β 1 ) : = ∑ i = 1 n ( Y i − β 0 − β 1 X i ) 2
( β 0 ^ , β 1 ^ ) = arg min β 0 , β 1 R S S ( β 0 , β 1 ) (\hat{\beta_0}, \hat{\beta_1}) = \argmin_{\beta_0, \beta_1} RSS(\beta_0, \beta_1) ( β 0 ^ , β 1 ^ ) = a r g m i n β 0 , β 1 R S S ( β 0 , β 1 )
위 식을 만족하는 estimator를 찾는 방식으로 uncertain coefficient를 estimate하게 됨
위 식을 partial derivative를 통해 계산하면,
β 0 ^ = Y ˉ − β 1 ^ X ˉ , β 1 ^ = s x y s x 2 \hat{\beta_0} = \bar{Y} - \hat{\beta_1}\bar{X} ,\ \ \ \ \ \ \hat{\beta_1}= \frac{s_{xy}}{s_x^2} β 0 ^ = Y ˉ − β 1 ^ X ˉ , β 1 ^ = s x 2 s x y
X ˉ = 1 n ∑ i = 1 n X i \bar{X} = \frac{1}{n}\sum^{n}_{i=1} X_i X ˉ = n 1 ∑ i = 1 n X i s x 2 = 1 n ( X i − X ˉ ) 2 s_x^2 = \frac{1}{n}(X_i-\bar{X})^2 s x 2 = n 1 ( X i − X ˉ ) 2 s x y = 1 n ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) s_{xy} = \frac{1}{n}\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y}) s x y = n 1 ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ )
RSS(Residual Sum of Squares)를 β 0 , β 1 \beta_0, \, \beta_1 β 0 , β 1
우리가 원하는 것은 prediction of Y \ Y Y
오차로써 거리 개념을 사용하는데, absolute value가 아닌 squares를 사용하는 이유 → 수학적 편리성 때문, 미분하기 쉬울 뿐 아니라 normal distribution에서의 MLE와 밀접하게 연관되어 있기 때문이다.
Multiple linear Model
simple linear model을 확장하여 random variable X 1 , X 2 , . . . , X p X_1, X_2, ... \ , X_p X 1 , X 2 , . . . , X p Y Y Y
y = β 0 + β 1 X 1 + β 2 X 2 + . . . + β p X p + ϵ y = \beta_0 + \beta_1X_1 +\beta_2X_2 + ... +\beta_pX_p + \epsilon y = β 0 + β 1 X 1 + β 2 X 2 + . . . + β p X p + ϵ
simple linear model과 마찬가지로
E [ Y ∣ X 1 = x 1 , . . . , X p = x p ] = β 0 + β 1 x 1 + . . . + β p x p \mathbb{E}[Y|X_1 = x_1, ...\, , X_p=x_p] = \beta_0 + \beta_1x_1 + ... + \beta_px_p E [ Y ∣ X 1 = x 1 , . . . , X p = x p ] = β 0 + β 1 x 1 + . . . + β p x p
since E [ ϵ ∣ X 1 = x 1 , . . . , X p = x p ] = 0 \mathbb{E}[\epsilon|X_1=x_1, ... \ , X_p=x_p] = 0 E [ ϵ ∣ X 1 = x 1 , . . . , X p = x p ] = 0
위 식에서 LHS는 X 1 , . . . , X p X_1, ... ,X_p X 1 , . . . , X p Y Y Y X i X_i X i Y Y Y
위 식이 말하고자 하는 것은 simple linear regression과 마찬가지로, the mean of Y Y Y X 1 , . . . , X p X_1, ... ,X_p X 1 , . . . , X p
β 0 \beta_0 β 0 Y Y Y X 1 = . . . = X p = 0 X_1 = ... =X_p = 0 X 1 = . . . = X p = 0 β 1 \beta_1 β 1 1 ≤ j ≤ p 1 \leq j \leq p 1 ≤ j ≤ p Y Y Y X j = x j X_j=x_j X j = x j X 1 , . . . , X j − 1 , X j + 1 , . . . , X p X_1, ... , X_{j-1} , X_{j+1}, ... , X_p X 1 , . . . , X j − 1 , X j + 1 , . . . , X p X j X_j X j X j X_j X j Y Y Y
multiple regression의 경우 dimension이 3-d 이상으로 확장되기 때문에 matrix를 이용한 접근이 필요하다.
이를 이용하여 간단히 표현하면,
β 0 , β 1 , . . . , β p \beta_0, \beta_1, ... ,\beta_p β 0 , β 1 , . . . , β p
R S S ( β ) : = ∑ i = 1 n ( Y i − β 0 − β 1 X i 1 − . . . − β p X i p ) 2 = ( Y − X β ) ′ ( Y − X β ) RSS(\beta) := \sum_{i=1}^{n}(Y_i-\beta_0-\beta_1X_{i1}-...-\beta_pX_{ip})^2 \\= (Y-X\beta)'(Y-X\beta) R S S ( β ) : = ∑ i = 1 n ( Y i − β 0 − β 1 X i 1 − . . . − β p X i p ) 2 = ( Y − X β ) ′ ( Y − X β )
위 RSS는 데이터의 β \beta β
→ least squares estimators are the minimizers of the RSS
β ^ : = arg min β ∈ R p + 1 R S S ( β ) \hat{\beta} := \argmin_{\beta\in\mathbb{R}^{p+1}} RSS(\beta) β ^ : = a r g m i n β ∈ R p + 1 R S S ( β )
RSS의 matrix form 덕분에,
β ^ = ( X ′ X ) − 1 X ′ Y \hat{\beta} = (X'X)^{-1}X'Y β ^ = ( X ′ X ) − 1 X ′ Y
위 식을 이용해 β ^ \hat{\beta} β ^
least squares estimates에 대해 닫힌 형태의 표현을 작성할 수 있다.
fitted values Y 1 ^ , . . . , Y n ^ \hat{Y_1}, ... , \hat{Y_n} Y 1 ^ , . . . , Y n ^
Y i ^ : = β 0 ^ + β 1 ^ X i 1 + . . . + β p ^ X i p , i = 1 , . . . n \hat{Y_i} := \hat{\beta_0} + \hat{\beta_1}X_{i1}+...+\hat{\beta_p}X_{ip},\ \ \ \ \ \ i= 1, ... \ n Y i ^ : = β 0 ^ + β 1 ^ X i 1 + . . . + β p ^ X i p , i = 1 , . . . n
→ they're the vertical projections of Y 1 , . . . , Y n Y_1, ... \ , Y_n Y 1 , . . . , Y n
매트릭스 폼으로 표현하면,
Y ^ = X β ^ = X ( X ′ X ) − 1 X ′ Y \hat{Y} = X\hat{\beta} = X(X'X)^{-1}X'Y Y ^ = X β ^ = X ( X ′ X ) − 1 X ′ Y
Assumptions of the model
linear Regression에서 estimator인 β ^ \hat{\beta} β ^ { ( X i , Y i ) } i = 1 n \{(X_i, \ Y_i)\}^n_{i=1} { ( X i , Y i ) } i = 1 n β \beta β
Assumptions of Linear Regression
Linearity (선형성):
→ E [ Y ∣ X 1 = x 1 , . . . , X p = x p ] = β 0 + β 1 x 1 + . . . + β p x p \mathbb{E}[Y|X_1=x_1, ... , X_p =x_p] = \beta_0 + \beta_1x_1 + ... + \beta_px_p E [ Y ∣ X 1 = x 1 , . . . , X p = x p ] = β 0 + β 1 x 1 + . . . + β p x p
Homoscedasticity (등분산성):
→ V a r [ ϵ ∣ X 1 = x 1 , . . . , X p = x p ] = σ 2 \mathbb{V}ar[\epsilon | X_1=x_1, ... ,\ X_p=x_p] = \sigma^2 V a r [ ϵ ∣ X 1 = x 1 , . . . , X p = x p ] = σ 2
Normality(정규성) : ϵ ∼ N ( 0 , σ 2 ) \epsilon \sim N(0, \sigma^2) ϵ ∼ N ( 0 , σ 2 )
Independence of the errors:
→ ϵ 1 , . . . , ϵ n \epsilon_1, ... ,\ \epsilon_n ϵ 1 , . . . , ϵ n E [ ϵ i ϵ j ] = 0 , i ≠ j \mathbb{E}[\epsilon_i\epsilon_j]=0, i \neq j E [ ϵ i ϵ j ] = 0 , i = j
since they are assumed to be normal
Y ∣ ( X 1 = x 1 , . . . , X p = x p ) ∼ N ( β 0 + β 1 x 1 + . . . + β p x p ) Y|(X_1=x_1, ... , X_p=x_p) \sim N(\beta_0+\beta_1x_1+ ... \ + \beta_px_p) Y ∣ ( X 1 = x 1 , . . . , X p = x p ) ∼ N ( β 0 + β 1 x 1 + . . . + β p x p )
위의 가정 중, 4번 가정을 제외하고 나머지는 표본의 관점에서의 가정이 아닌, 확률변수(즉, 모수) 에 관한 가정
이러한 가정들을 기반으로, 선형회귀 모델을 다시 표현하면
Y i ∣ ( X i 1 = x i 1 , . . . , X i p = x i p ) ∼ N ( β 0 + β 1 x i 1 + . . . + β p x i p , σ 2 ) Y_i|(X_{i1}=x_{i1}, ... , X_{ip}=x_{ip}) \sim N(\beta_0+\beta_1x_{i1}+ ... \ + \beta_px_{ip} \, , \ \sigma^2) Y i ∣ ( X i 1 = x i 1 , . . . , X i p = x i p ) ∼ N ( β 0 + β 1 x i 1 + . . . + β p x i p , σ 2 )
with Y 1 , . . . , Y n Y_1, \ ... \ , Y_n Y 1 , . . . , Y n
Y ∣ X ∼ N n ( X β , σ 2 I ) Y|X \sim N_n(X\beta, \sigma^2I) Y ∣ X ∼ N n ( X β , σ 2 I )
Least squares and Maximum Likelihood Estimation
Least squares는 linear models에서 아주 중요한 역할을 담당한다. 그런데, Least Squares는 데이터에서 어떠한 plane을 fitting하는데 필요한 단순한 geometrical argument처럼 보일 수 있다.β \beta β
→ 하지만, 사실 least squares estimation은 위에서 가정했던 4개의 assumption 하에서 maximum likelihood estimation과 동일하다.
Y i ∣ ( X i 1 = x i 1 , . . . , X i p = x i p ) ∼ N ( β 0 + β 1 x i 1 + . . . + β p x i p , σ 2 ) Y_i|(X_{i1}=x_{i1}, ... , X_{ip}=x_{ip}) \sim N(\beta_0+\beta_1x_{i1}+ ... \ + \beta_px_{ip} \, , \ \sigma^2) Y i ∣ ( X i 1 = x i 1 , . . . , X i p = x i p ) ∼ N ( β 0 + β 1 x i 1 + . . . + β p x i p , σ 2 )
Y ∣ X ∼ N n ( X β , σ 2 I ) Y|X \sim N_n(X\beta, \ \sigma^2I) Y ∣ X ∼ N n ( X β , σ 2 I )
위 식으로부터 Y 1 , . . . , Y n Y_1, ... \ , Y_n Y 1 , . . . , Y n
ℓ ( β ) = log ( ϕ ( Y ; X β , σ 2 I ) ) = ∑ i = 1 n log ( ϕ ( Y i ; ( X β ) i , σ ) ) \ell(\beta) = \log(\phi(Y;X\beta, \sigma^2\mathbf{I})) = \sum_{i=1}^{n}\log(\phi(Y_i;(X\beta)_i, \sigma)) ℓ ( β ) = log ( ϕ ( Y ; X β , σ 2 I ) ) = ∑ i = 1 n log ( ϕ ( Y i ; ( X β ) i , σ ) )
위 ℓ ( β ) \ell (\beta) ℓ ( β ) β \beta β β ^ M L \hat{\beta}_{ML} β ^ M L
β ^ M L = arg max β ∈ R p + 1 ℓ ( β ) = ( X ′ X ) − 1 X Y \hat{\beta}_{ML} = \argmax_{\beta\in\mathbb{R}^{p+1}}\ell(\beta) = (X'X)^{-1}XY β ^ M L = a r g m a x β ∈ R p + 1 ℓ ( β ) = ( X ′ X ) − 1 X Y
Proof)
ℓ ( β ) = − log ( ( 2 π ) n / 2 σ n ) − 1 2 σ 2 ( Y − X β ) ′ ( Y − X β ) \ell(\beta) = -\log((2\pi)^{n/2}\sigma^n) \ -\frac{1}{2\sigma^2}(Y-X\beta)'(Y-X\beta) ℓ ( β ) = − log ( ( 2 π ) n / 2 σ n ) − 2 σ 2 1 ( Y − X β ) ′ ( Y − X β )
differentiate with respect to β \beta β
1 σ 2 ( Y − X β ) ′ X = 1 σ 2 ( Y ′ X − β ′ X ′ X ) = 0 \frac{1}{\sigma^2}(Y-X\beta)'X = \frac{1}{\sigma^2}(Y'X-\beta'X'X) = 0 σ 2 1 ( Y − X β ) ′ X = σ 2 1 ( Y ′ X − β ′ X ′ X ) = 0
β ^ = ( X ′ X ) − 1 X Y \hat{\beta} = (X'X)^{-1}XY β ^ = ( X ′ X ) − 1 X Y
MLE(Maximum Likelihood Estimation)에 대한 직관적인 접근
MLE는 Likelihood를 최대화 하는 모델의 파라미터들의 값을 결정하는 방법
만약 linear regression이라고 한다면,
우리는 parameter α , β \alpha, \beta α , β x x x y y y y ( x ∣ α , β ) y(x|\alpha, \beta) y ( x ∣ α , β ) x x x y ( x ∣ α , β ) y(x|\alpha, \beta) y ( x ∣ α , β ) y y y α , β \alpha, \beta α , β
이러한 parameter들은 여러개일 수도 있고 각 모델마다 다른 형태를 가지게 된다. (이런 parameter들을 θ \theta θ
parameter들을 잘 학습하여 모델 y ( x ∣ θ ) y(x|\theta) y ( x ∣ θ )
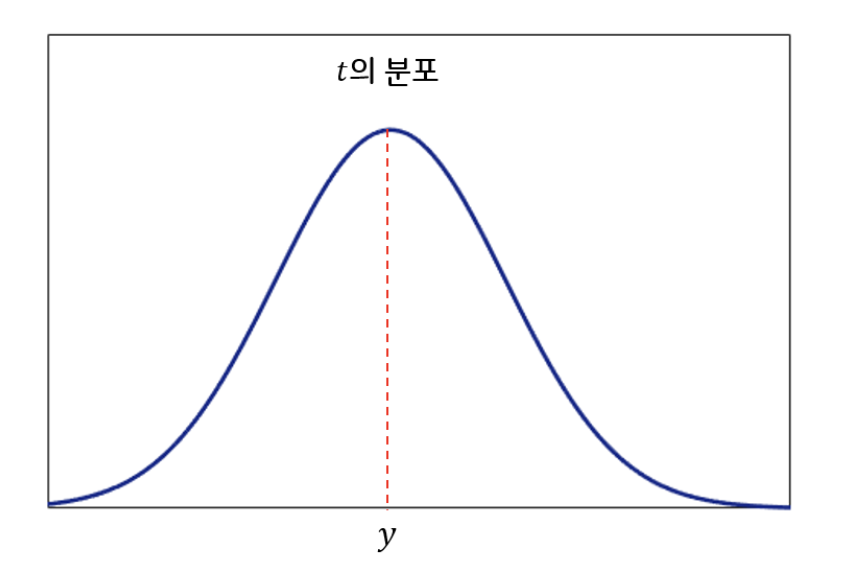
우리는 x x x t t t
t = y ( x ∣ θ ) t = y(x|\theta) t = y ( x ∣ θ )
그런데, 우리는 항상 t = y ( x ∣ θ ) t = y(x|\theta) t = y ( x ∣ θ )
데이터의 형태가 우리가 가정한 모델의 형태와 다르기 때문에 필연적으로 오차가 발생한다.
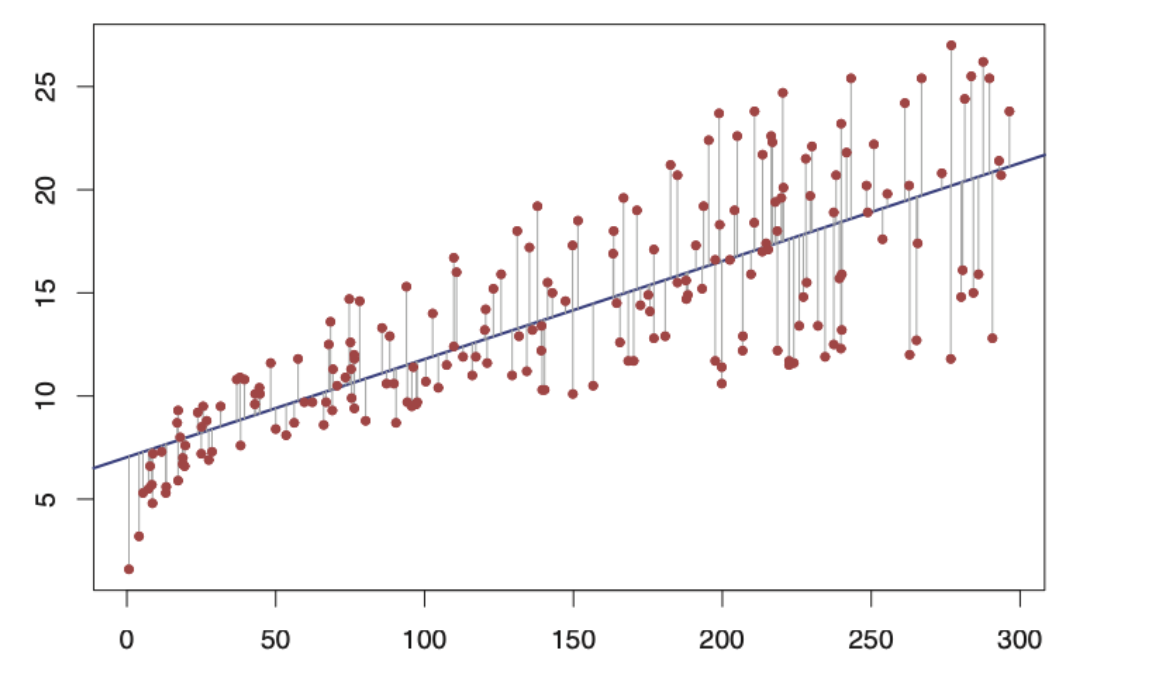
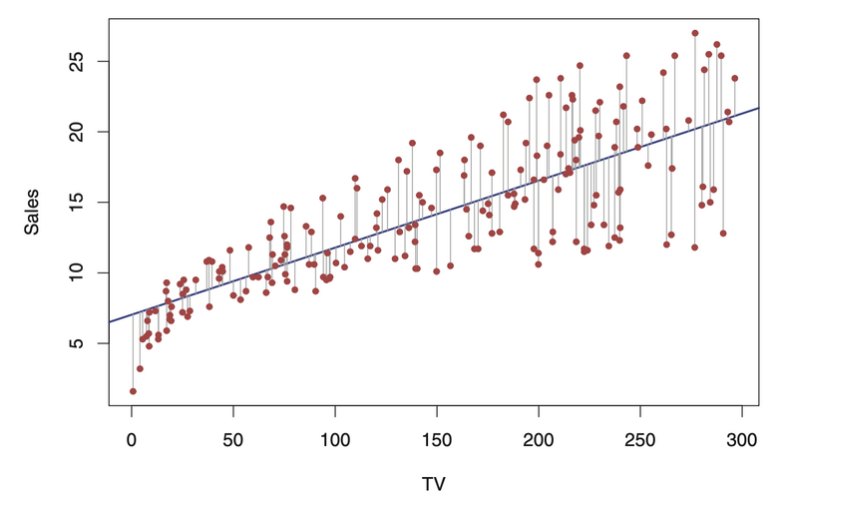
이러한 불확실성을 TV 광고와 판매량(Sales)을 예로 들어 통계적으로 표현하면
'특정 advertisement budget(x x x y y y
그리고 이 직선은 assumption에 기반하여,
β 0 + β 1 x i 1 + . . . + β p x i p \beta_0+\beta_1x_{i1}+...+\beta_px_{ip} β 0 + β 1 x i 1 + . . . + β p x i p σ \sigma σ
라고 말할 수 있다.
Y i ∣ ( X i 1 = x i 1 , . . . , X i p = x i p ) ∼ N ( β 0 + β 1 x i 1 + . . . + β p x i p , σ 2 ) Y_i|(X_{i1}=x_{i1}, ... , X_{ip}=x_{ip}) \sim N(\beta_0+\beta_1x_{i1}+ ... \ + \beta_px_{ip} \, , \ \sigma^2) Y i ∣ ( X i 1 = x i 1 , . . . , X i p = x i p ) ∼ N ( β 0 + β 1 x i 1 + . . . + β p x i p , σ 2 )
여기서, 우리가 Normal Distribution이라는 확률분포를 이용하는 이유는, 우리가 한 예측에 대해 100% 확신할 수 없기 때문이다. Normal Distribution이라는 확률분포를 통해서, '우리의 예측하는
Y ^ \hat{Y} Y ^
위 식을 이용해서 Maximum Likelihood Estimation을 하기 위해
우선 위 Normal Distribution의 p.d.f를 이용해 Likelihood를 정의하면 ,
p ( β X , σ 2 ∣ x ) = 1 2 π σ e − ( y − β X ) 2 2 σ 2 p(\beta X, \sigma^2|x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(y-\beta X)^2}{2\sigma^2}} p ( β X , σ 2 ∣ x ) = 2 π σ 1 e − 2 σ 2 ( y − β X ) 2
위 식이 된다. 우리는 parameter인 μ ( β X ) \mu (\beta X) μ ( β X ) σ 2 \sigma^2 σ 2
이러한 상황에서 y y y
모든 x ( x 1 , x 2 , . . . , x n ) x (x_1, x_2, ... , x_n) x ( x 1 , x 2 , . . . , x n ) y ( y 1 , y 2 , . . . , y n ) y(y_1, y_2, ... , y_n) y ( y 1 , y 2 , . . . , y n )
p ( β X , σ 2 ∣ x ) = 1 2 π σ e − ( y − β X ) 2 2 σ 2 p(\beta X, \sigma^2|x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(y-\beta X)^2}{2\sigma^2}} p ( β X , σ 2 ∣ x ) = 2 π σ 1 e − 2 σ 2 ( y − β X ) 2
그래서 우리는 Probability Distribution을 이용해서 Likelihood를 정의하고, 이를 최대화하는 모델을 optimal한 모델로 보고, 이를 찾게 된다.
Maximum Likelihood Estimation for the Normal Distribution
probability vs. likelihood
probability : the quantity most people are familiar with which deals with predicting new data given a known model ( 동전 던지기를 할 때 앞면이 나올 확률은? )
p ( d a t a ∣ d i s t r i b u t i o n ) p( data | distribution) p ( d a t a ∣ d i s t r i b u t i o n )
likelihood : deals with fitting models given some known data ( 던진 동전이 6회 연속 앞면이 나왔는데, 이 동전이 비정상 동전일 확률은 ? )
p ( d i s t r i b u t i o n ∣ d a t a ) p(distribution | data) p ( d i s t r i b u t i o n ∣ d a t a )
즉, 모델의 파라미터가 이미 정해져 있고, 새로운 데이터에 대한 quantity를 도출하는 것이 probability 이고, 모델의 파라미터가 정해져 있지 않고, 주어진 데이터를 통해서 모델을 fitting하기 위해 도출한 quantity가 likelihood 이다.
p ( x ∣ θ ) = p(x|\theta) = p ( x ∣ θ ) = p ( x ∣ μ , σ ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 p(x|\mu, \sigma) = \frac {1} {\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} p ( x ∣ μ , σ ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2
정규분포에는 μ , σ \mu, \sigma μ , σ μ \mu μ σ \sigma σ
parameter가 2개이기 때문에, 우리는 1개를 각각 따로 구하되, 다른 하나는 고정되어 있다고 가정하고 계산한다.
L ( μ , σ ∣ x 1 , x 2 , . . . , x n ) = L ( μ , σ ∣ x 1 ) × . . . × L ( μ , σ ∣ x n ) = 1 2 π σ 2 e − ( x 1 − μ ) 2 / 2 σ 2 × . . . × 1 2 π σ 2 e − ( x n − μ ) 2 / 2 σ 2 L(\mu, \sigma | x_1, x_2, ... ,x_n) = L(\mu, \sigma |x_1) \times ... \times L(\mu, \sigma |x_n) \\ = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x_1-\mu)^2/2\sigma^2} \times ... \times \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x_n-\mu)^2/2\sigma^2} L ( μ , σ ∣ x 1 , x 2 , . . . , x n ) = L ( μ , σ ∣ x 1 ) × . . . × L ( μ , σ ∣ x n ) = 2 π σ 2 1 e − ( x 1 − μ ) 2 / 2 σ 2 × . . . × 2 π σ 2 1 e − ( x n − μ ) 2 / 2 σ 2
ln [ L ( μ , σ ∣ x 1 , x 2 , . . . , x n ) ] = ln ( 1 2 π σ 2 e − ( x 1 − μ ) 2 / 2 σ 2 × . . . × 1 2 π σ 2 e − ( x n − μ ) 2 / 2 σ 2 ) = − 1 2 ln ( 2 π ) − ln ( σ ) − ( x 1 − μ ) 2 2 σ 2 − . . . − 1 2 ln ( 2 π ) − ln ( σ ) − ( x n − μ ) 2 2 σ 2 \ln [L(\mu, \sigma | x_1, x_2, ... ,x_n)] = \ln(\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x_1-\mu)^2/2\sigma^2} \times ... \times \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x_n-\mu)^2/2\sigma^2}) \\ = -\frac{1}{2}\ln(2\pi)-\ln(\sigma)-\frac{(x_1-\mu)^2}{2\sigma^2} - ... -\frac{1}{2}\ln(2\pi)-\ln(\sigma)-\frac{(x_n-\mu)^2}{2\sigma^2} ln [ L ( μ , σ ∣ x 1 , x 2 , . . . , x n ) ] = ln ( 2 π σ 2 1 e − ( x 1 − μ ) 2 / 2 σ 2 × . . . × 2 π σ 2 1 e − ( x n − μ ) 2 / 2 σ 2 ) = − 2 1 ln ( 2 π ) − ln ( σ ) − 2 σ 2 ( x 1 − μ ) 2 − . . . − 2 1 ln ( 2 π ) − ln ( σ ) − 2 σ 2 ( x n − μ ) 2 ∂ ∂ μ ln [ L ( μ , σ ∣ x 1 , . . . , x n ) ] = 0 − 0 + ( x 1 − μ ) σ 2 + . . . + ( x n − μ ) σ 2 = 1 σ 2 [ ( x 1 + . . . + x n ) − n μ ] \frac{\partial}{\partial\mu}\ln[L(\mu,\sigma|x_1, ..., x_n)] = 0 - 0 + \frac{(x_1-\mu)}{\sigma^2} + ... + \frac{(x_n-\mu)}{\sigma^2} \\ = \frac{1}{\sigma^2}[(x_1+...+x_n) - n\mu] ∂ μ ∂ ln [ L ( μ , σ ∣ x 1 , . . . , x n ) ] = 0 − 0 + σ 2 ( x 1 − μ ) + . . . + σ 2 ( x n − μ ) = σ 2 1 [ ( x 1 + . . . + x n ) − n μ ] 0 = 1 σ 2 [ ( x 1 + . . . + x n ) − n μ ] 0 = ( x 1 + . . . + x n ) − n μ n μ = ( x 1 + . . . + x n ) ∴ μ = ( x 1 + . . . + x n ) n 0 = \frac{1}{\sigma^2}[(x_1+...+x_n) - n\mu] \\0 = (x_1+...+x_n) - n\mu \\ n\mu = (x_1+...+x_n) \\ \therefore \mu = \frac{(x_1+...+x_n)}{n} 0 = σ 2 1 [ ( x 1 + . . . + x n ) − n μ ] 0 = ( x 1 + . . . + x n ) − n μ n μ = ( x 1 + . . . + x n ) ∴ μ = n ( x 1 + . . . + x n )
∂ ∂ σ ln [ L ( μ , σ ∣ x 1 , . . . , x n ) ] = 0 − n σ + ( x 1 − μ ) 2 σ 3 + . . . + ( x n − μ ) 2 σ 3 = − n σ + 1 σ 3 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] \frac{\partial}{\partial\sigma}\ln[L(\mu, \sigma | x_1, ... ,x_n)] = 0 - \frac{n}{\sigma} +\frac{(x_1-\mu)^2}{\sigma^3} + ... + \frac{(x_n - \mu)^2}{\sigma^3} \\ = -\frac{n}{\sigma} + \frac{1}{\sigma^3}[(x_1-\mu)^2+...+(x_n-\mu)^2] ∂ σ ∂ ln [ L ( μ , σ ∣ x 1 , . . . , x n ) ] = 0 − σ n + σ 3 ( x 1 − μ ) 2 + . . . + σ 3 ( x n − μ ) 2 = − σ n + σ 3 1 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] 0 = − n σ + 1 σ 3 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] 0 = − n + 1 σ 2 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] n = 1 σ 2 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] n σ 2 = ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 σ 2 = ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 n ∴ σ = ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 n 0 = -\frac{n}{\sigma} + \frac{1}{\sigma^3}[(x_1-\mu)^2+...+(x_n-\mu)^2] \\ 0 = -n + \frac{1}{\sigma^2}[(x_1-\mu)^2+...+(x_n-\mu)^2] \\ n = \frac{1}{\sigma^2}[(x_1-\mu)^2+...+(x_n-\mu)^2] \\ n\sigma^2 = (x_1-\mu)^2 + ... + (x_n -\mu)^2 \\ \sigma^2 = \frac{(x_1-\mu)^2+...+(x_n-\mu)^2}{n} \\ \therefore \sigma = \sqrt{\frac{(x_1-\mu)^2+...+(x_n-\mu)^2}{n}} 0 = − σ n + σ 3 1 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] 0 = − n + σ 2 1 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] n = σ 2 1 [ ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ] n σ 2 = ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 σ 2 = n ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2 ∴ σ = n ( x 1 − μ ) 2 + . . . + ( x n − μ ) 2