1182 부분 수열의 합 구하기

문제

N개의 정수로 이루어진 수열이 있을 때, 크기가 양수인 부분수열 중에서 그 수열의 원소를 다 더한 값이 S가 되는 경우의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 정수의 개수를 나타내는 N과 정수 S가 주어진다. (1 ≤ N ≤ 20, |S| ≤ 1,000,000) 둘째 줄에 N개의 정수가 빈 칸을 사이에 두고 주어진다. 주어지는 정수의 절댓값은 100,000을 넘지 않는다.

5 0
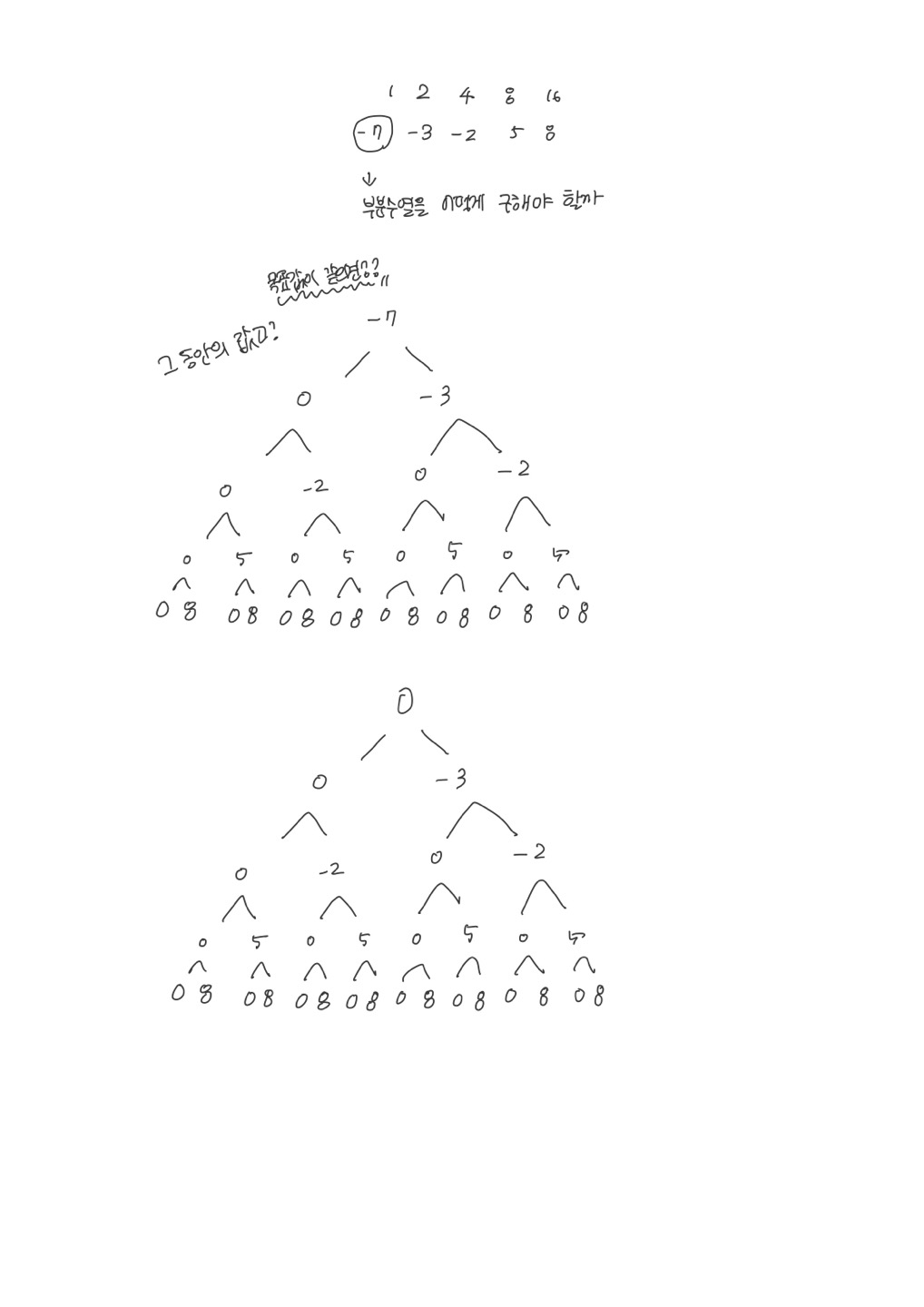
-7 -3 -2 5 8

출력

첫째 줄에 합이 S가 되는 부분수열의 개수를 출력한다.

1

문제풀이 (1) 재귀

재귀함수를 통해서 트리구조로 검색을 한다면 모든 경우의 수를 빠르게 돌 수 있다.

간단히 재귀함수를 사용해서 풀이를 했고, 백트래킹은 구현하지 못했다.

이게 왜 백트래킹인지도 의문!이긴 하다.

그리고 중간에 count += 1을 하는게 의문이들었다. 왠지 이후에 -1, +1 이 오면 중복이 될 것 같다고 느낌이 들었다.

그러나 수열은 서로 다른 값이 있거나, 크기가 다르면결국 다른 수열이기 때문에 -1 , +1이 포함되는 순간 다른 부분 수열이었다.

그리고 왠지 트리구조로 그리니까, 모두 n개의 수열로 고정되어있다고 느낌이 들었따. (그놈의 느낌^^) 그러나, 중간중간 검사를 하기 때문에 가능한 모든 개수의 부분수열을 계산할 수 있었다.

(아래는 이해를 위해서 직접 그린 표)

정답 코드

#부분수열의 합

x = list(map(int, input().split(" ")))
a_lsit = list(map(int, input().split(" ")))

count = 0
def find_sum(i,temp):
    global count
    if i < len(a_lsit):
        temp += a_lsit[i]

        if temp == x[1]:
            count += 1

        find_sum(i+1,temp)
        find_sum(i+1,temp - a_lsit[i])
    else:
        return

find_sum(0,0)
print(count)

문제풀이 (2) 파이썬의 조합이용 combinations

#부분수열의 합
#파이썬의 조합 구하기 함수 이용
from itertools import combinations

x = list(map(int, input().split(" ")))
a_lsit = list(map(int, input().split(" ")))
count = 0

for i in range(x[0]):
    com = combinations(a_lsit,i+1)

    for j in com:
        if sum(j) == x[1]:
            count += 1

print(count)