11725 - BFS

문제

루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 노드의 개수 N (2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에 트리 상에서 연결된 두 정점이 주어진다.

출력

첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.

예제 입력 1

7
1 6
6 3
3 5
4 1
2 4
4 7

예제 출력 1

4
6
1
3
1
4

문제풀이

• BFS 도입하기 : 부모 노드 체크해주기
• 그래프 만들어주기

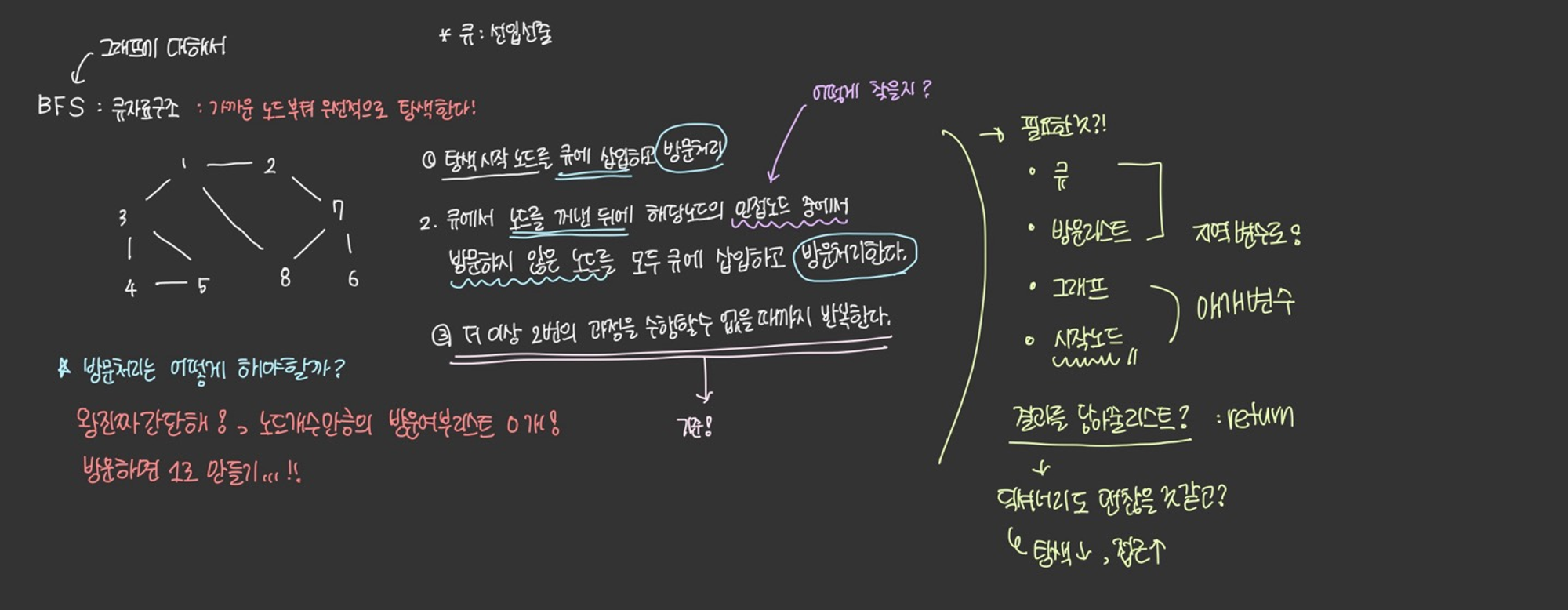
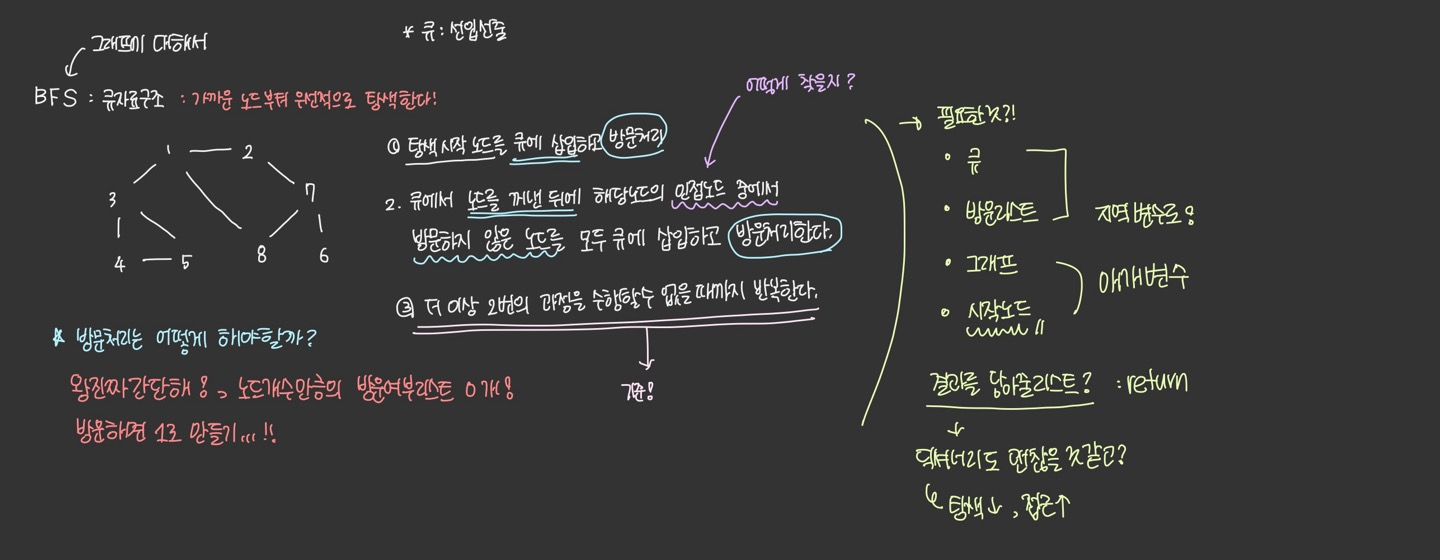
BFS란?

BFS

그래프를 전체 탐색하는 방법 중 하나로, 가까운 노드부터 탐색해 모든 노드에 딱 한번씩만 들리는 방법이다.

트리구조가 아니여도 탐색할 수 있다.

그래프와 탐색시작노드, 큐만 있다면!!

큐를 왜쓸까? : 다음에 탐색해야할 노드를 넣어놓는 바구니로!

BFS 과정

• 탐색 시작 노드를 큐에 삽입하고 방문처리
• 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리한다.
• 큐에 아무것도 남아있지 않을때까지 반복한다.

왜 BFS가 빠를까??

모든 노드를 순회하는 것이 아니라, 이미 간 노드는 순회하지 않기 떄문이다.
→ 방문처리를 통해서

방문 처리를 하는 방법

노드의 개수만큼 방문리스트를 만들어서 노드의 값을 인덱스로 가지는 요소에 표시, 딕셔너리 이용등등…

그래프를 만드는 방법

: 노드마다 연결된 노드를 모두 표현

[

(1) [1,2,3]

(2) [1]

(3) [3]

]

코드로 살펴보기

그래프 만드는 코드

graph = [[] for i in range(n)]
for i in range(n-1):
    a = list(map(int,sys.stdin.readline().strip().split(" ")))
    graph[a[0]-1].append(a[1])
    graph[a[1]-1].append(a[0])

BFS 살펴보기

• 탐색 시작 노드를 큐에 삽입하고 방문처리
• 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리한다.

필요한 것: 큐, 시작노드, 방문처리용 리스트

def bfs(graph, start):
    parent_node_list = [0] * len(graph)
    que = deque() #검사할 노드를 담는 큐
    que.append(start) #시작 노드를 큐에 담기 
    parent_node_list[start - 1] = 1  #부모노드를 표현하는 리스트 + 방문여부를 표시

    while que:   #큐에 아무것도 안남을 때까지
        target_node = que.popleft() #검색노드 꺼내기!
        for i in graph[target_node -1]: #노드와 연결된 다른 노드에 대해서 검사시작
            if parent_node_list[i - 1] == 0: # 방문하지 않은 노드에 대해서만 시작
                que.append(i) #방문하지 않은 노드는  이후 순차 검색의 개상으로 큐에 넣어주기
                parent_node_list[i-1] = target_node #방문처리를 해주기 (부모의 노드를 넣어줌)
    return parent_node_list

출력하는 부분

for i in range(1,len(parent_node_list)):
    print(parent_node_list[i])

# 트리의 부모 찾기
import sys
from collections import deque
def bfs(graph, start):
    parent_node_list = [0] * len(graph)
    que = deque()
    que.append(start)
    parent_node_list[start - 1] = 1

    while que:
        target_node = que.popleft()
        for i in graph[target_node -1]:
            if parent_node_list[i - 1] == 0:
                que.append(i)
                parent_node_list[i-1] = target_node
    return parent_node_list

n = int(sys.stdin.readline().strip())
graph = [[] for i in range(n)]
for i in range(n-1):
    a = list(map(int,sys.stdin.readline().strip().split(" ")))
    graph[a[0]-1].append(a[1])
    graph[a[1]-1].append(a[0])

# print(graph)
#부모노드리스트를 리턴받자

parent_node_list = bfs(graph, 1)

for i in range(1,len(parent_node_list)):
    print(parent_node_list[i])