[CS]자료형

초심으로 돌아가서 자료형을 공부하면서 연관되는 개념까지 싸그리 학습해보자

자료형

자료형(Data Type) : 데이터를 구성하고 관리하는 기본 개념으로, 데이터의 크기, 형식, 해석 방식을 정의한다.

자료형의 분류

원시자료형(Primitive Types) : 데이터 표현의 가장 기본적인 형태

정수형(Integer Types)
정수를 저장하는 자료형
값의 범위는 비트 수와 부호(sign)의 유무에 따라 달라진다.
- byte : 1 byte
- int : 2byte
- short : 4byte
- long : 8byte

부호 ?
- 숫자의 양수(Positive) 또는 음수(Negative) 여부를 나타내는 개념
- 가장 왼쪽의 비트(최상위 비트)를 부호 비트(Sign Bit)로 사용한다.
- 0 이 양수(Positive)
- 1 이 음수(Negative)

비트 ?
- 비트(Binary Digit)는 컴퓨터에서 데이터를 표현하는 가장 작은 단위.
- 0 또는 1 두 가지 상태만 가질 수 있음(0 = OFF, 1 = ON)
- 컴퓨터는 모든 데이터를 2진수로 처리하고, 각각의 비트는 2진법의 자리값을 나타낸다. 모든 데이터(숫자, 문자, 이미지 등)는 비트의 조합으로 표현된다.

바이트 ?
- 8비트로 구성된 데이터 저장 단위로 2⁸ = 256개의 값(0~255 or -128~127)을 표현 가능하다.

인코딩 디코딩 ?
- 인코딩(Encoding) : 데이터를 다른 형식으로 변환하는 과정으로 문자 인코딩의 경우 텍스트 데이터를 숫자로 변환해서 컴퓨터가 저장하고 처리할 수 있도록 한다.
- 디코딩(Decoding) : 인코딩된 데이터를 원래의 형식으로 복원하는 과정으로 이진수, 압축파일, 암호화된 데이터 등 컴퓨터가 처리 가능한 데이터를 사람이 읽을 수 있는 형태로 되돌리는 작업* 문자 인코딩 ?
- 컴퓨터가 문자를 숫자로 변환해서 저장하고 처리하기 위한 인코딩 체계.

문자 인코딩 ?
- ASCII(American Standard Code for Information Interchange) : 미국 표준 문자 인코딩 체계로, 주로 영어 알파벳, 숫자, 특수 문자 등을 포함함. 초창기 문자 인코딩 방식
- Unicode : 모든 언어와 문자를 표현할 수 있도록 설계된 국제 표준 문자 인코딩 체계

인코딩 방식으로는 EUC-KR, UTF-8, UTF-16, UTF-32 등이 있음

실수형(Floating-Point Types)
- 소수점을 포함하는 숫자를 표현
- float(Single Precision) : 32비트
- double(Double Precision) : 64비트
문자형(Character Types)
- 단일 문자를 표현. ASCII 혹은 Unicode 사용
ASCII : 1 Byte
Unicode : 2 Byte
논리형(Boolean Type)
- true or false 두 가지 상태만 표현
보통 1 Bit

// Java
참조 자료형(Reference Type) : 기본 자료형을 조합하거나 확장해서 더 복잡한 데이터를 표현하는 자료형

배열(Array)
- 동일한 자료형의 데이터 집합을 순차적으로 저장한 자료형
고정된 크기를 가지고, 각 요소는 인덱스를 통해 접근함.
메모리에 연속적으로 저장되고, 모든 요소가 같은 자료형이어야 함.
클래스(Class)
- 객체 지향 프로그래밍(Object-Oriented Programming) 에서 속성과 메서드를 포함하는 사용자 정의 자료형
데이터를 캡슐화하고 메서드를 통해 조작함.
객체를 생성해서 실제 데이터를 저장하고 사용할 수 있음.

자료형 설계의 한계

1. 값의 범위 제한 : 오버플로우 또는 언더플로우 발생 가능
2. 실수 표현에서의 오차 : 부동소수점 연산에서 근사값으로 인해 오차가 발생 가능
3. 타입 변환 문제 : 서로 다른 타입 간의 변환시에 정밀도가 손실됨
4. Null 값의 문제 : 참조타입에서 Null 값으로 인해 NullPointerException 과 같은 런타임 에러 발생 가능
5. 메모리 비효율 : 실제 데이터 크기에 비해 메모리를 낭비할 수 있음

오버플로우 : 데이터가 표현할 수 있는 최대값을 초과했을 때 발생하는 현상
언더플로우 : 데이터가 표현할 수 있는 최소값보다 더 작은 값으로 감소할때 발생

컴퓨터 메모리

코드
실행할 프로그램의 코드가 저장되는 영역으로 텍스트 영역이라고 불림.
CPU 가 코드 영역에 저장된 명령어를 하나씩 가져가서 처리함

데이터 영역
프로그램의 전역 변수와 정적(static) 변수가 저장되는 영역
데이터 영역은 프로그램의 시작과 함께 할당되고 프로그램이 종료되면 소멸함.

스택 영역
정적 메모리 영역. 함수 호출, 지역 변수 관리 등에 사용함.
push 동작으로 데이터를 저장, pop 동작으로 데이터를 인출하는 LIFO(Last In, First Out) 원칙으로 데이터를 관리함.
고정 크기이고, 빠른 메모리 할당과 해제가 특징임.
스택의 크기는 제한적이며, 이를 초과하면 스택 오버플로우가 발생할 수 있음

스택 오버플로우(Stack Overflow) : 함수의 재귀 호출이 무한히 반복되면 해당 프로그램이 스택 오버플로우에 의해 종료됨
재귀 호출에 의한 스택 프레임이 점차 쌓이게 되다가 스택의 공간보다 더 큰 데이터가 push 되면 프로그램은 에러를 발생하고 강제종료 시킴.

힙 영역
동적 메모리 영역. 런타임시 크기가 동적으로 결정되는 데이터를 저장.
비정렬(non-ordered) 메모리 구조로, 메모리 할당과 해제가 스택보다 느림
가변 크기의 데이터와 객체를 저장함.
사용자가 직접 관리할 수 있다는 장점이 있으나, 동시에 관리를 해야 한다는 까다로움 또한 있음.
힙 영역은 메모리의 낮은 주소에서 높은 주소 방향으로 할당됨
힙 메모리를 잘 관리하지 못하면 프로그램에 메모리 누수(Memory Leak)가 발생할 수 있음.

가비지 컬렉션(Garbage Collection)
힙 영역에서 동적으로 할당했던 메모리 영역 중 필요가 없어진 메모리 영역을 주기적으로 삭제하는 프로세스
Java 는 JVM 에 탑재된 가비지 컬렉터가 메모리 관리를 대신 해줌

자료구조

자료구조(Data Structure)
- 데이터를 효율적으로 저장, 관리, 처리하기 위한 구조적 방식으로 데이터를 논리적이고 체계적으로 조직화해서 작업을 효율적으로 수행할 수 있게 도움.

자료구조 특징

효율성 : 데이터의 삽입, 삭제, 검색, 정렬 등의 상황또는 문제에 알맞은 자료구조 사용시 처리 효율이 증가
조직화 : 자료구조는 데이터를 논리적 또는 물리적으로 구조화해서 저장함. 이러한 데이터의 관계와 배치를 정의해서 효율적으로 접근하고 처리할 수 있음.
자료의 추상화(Abstraction) : 복잡한 시스템의 세부적인 구현을 숨기고, 필요한 핵심 개념 혹은 기능만을 노출해서 단순화하는 과정
간결성, 재사용성, 유지보수 면에서 우수함

자료구조 분류

단순구조(Simple Structure)
가장 기본적이고 간단한 형태의 자료구조. 데이터의 구조적 관계가 없는 개별적인 데이터 항목을 처리하는데 사용
- 정수(Integer), 실수(Floating Poing), 문자(Character), 문자열(String), 논리(Boolean) 등

선형구조(Linear Structure)
데이터가 순차적으로 배치되는 자료구조. 데이터가 메모리에 연속적이거나 논리적으로 연결되어 있고, 각 요소는 이전 요소와 다음 요소에 대한 관계를 가짐. 데이터가 특정 순서로 접근되거나 처리될 때 사용

배열(Array)

데이터가 메모리에 연속적으로 저장되는 자료구조.
특징
- 고정 크기 : 선언시 크기가 고정됨.
- 연속적인 메모리 : 배열 요소는 메모리상에 연속적으로 배치됨. 인덱스를 사용하면 O(1) 시간 복잡도로 특정 요소에 접근 가능
- 자료형 동일 : 배열에 저장되는 모든 요소는 동일한 자료형이어야 함.
- 순차 접근 : 배열 요소는 인덱스를 사용해 순차적 또는 랜덤으로 접근 가능함.

연결 리스트(Linked List)

각 노드(Node) 들이 데이터와 포인터를 가지고 논리적으로 연결된 구조
특징
- 포인터로 다음 노드를 찾을 수 있음.
- 크기가 동적으로 변경 가능
- 데이터 접근은 순차적이고, 삽입/삭제 동작이 빠름
종류
- 단일 연결 리스트(Singly Linked List) : 한방향 연결
- 이중 연결 리스트(Doubly Linked List) : 양방향 연결
- 원형 연결 리스트(Circular Linked List) : 마지막 노드가 첫번째 노드를 가리킴

스택(Stack)

한쪽 끝에서만 데이터를 넣고 뺄 수 있는 LIFO(Last In First Out) 원칙에 따라 동작하는 선형구조
동작
1. push : 스택에 데이터를 추가하는 연산. 스택의 맨 위에 데이터 삽입
2. pop : 스택에서 데이터를 제거하는 연산. 스택의 맨 위에서 데이터를 삭제하고 반환
3. peek or top : 스택의 맨 위에 있는 데이터를 반환. 스택에서 제거하지는 않음
4. isEmpty : 스택이 비어있는지 확인하는 연산
5. size : 스택에 저장된 데이터의 개수 반환

큐(Queue)

양쪽 끝에서만 삽입, 삭제가 일어나는 FIFO(First In First Out) 원칙에 따라 동작하는 자료구조. 리어(rear) 에서 삽입, 프론트(front) 에서 삭제
* 중간 항목에 접근하기 어렵고, 특정 항목을 찾기 위해 큐를 선형적으로 탐색해야 하기에 큐의 크기에 탐색 시간이 비례함.
동작
1. enqueue(item) : 큐의 리어(rear)에 item 삽입하는 연산
2. dequeue() : 큐의 프론트(front)에서 항목을 삭제하고 반환하는 연산
3. isEmpty() : 큐가 비어있는지 확인하는 연산
4. size() : 큐의 현재 크기를 반환
5. peek() : 큐의 프론트(front)에 위치한 항목 반환. 큐에서 삭제하지는 않음

비선형구조
데이터가 계층적이거나 복잡한 연결 관계를 가지는 자료구조. 데이터간의 관계를 명확히 표현하거나 복잡한 문제를 효율적으로 해결하는데 사용됨.

트리(Tree)

계층적 관계를 가지는 비선형 자료구조. 노드(Node) 와 간선(Edge) 로 구성됨
종류
1. 일반 트리(General Tree) : 각 노드가 여러 자식을 가질 수 있는 트리
2. 이진 트리(Binary Tree) : 각 노드의 차수가 2 이하인 트리
3. 이진 탐색 트리(Binary Search Tree, BST) : 순서화된 이진 트리로 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며, 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 함.
외에도 모든 노드가 자식을 하나만 가지는 편향 트리(skew tree), 데이터베이스 인덱싱을 구현하는데 사용하는 AVL tree, B-tree, B+tree, 사전 저장에 사용되는 tries, Heap 등이 있음

그래프(Graph)

연결되어있는 원소간의 관계를 표현한 비선형 자료구조.
연결할 객체를 나타내는 정점(Vertex)과 객체를 연결하는 간선(Edge)의 집합으로 구성
G=(V, E) 로 정의하는데, V 는 정점의 집합, E 는 간선들의 집합을 의미
용어
차수(Degree) : 정점에 부속되어 있는 간선의 수
-진입차수(in-degree) : 정점을 머리로 하는 간선의 수
-진출차수(out-degree) : 정점을 꼬리로 하는 간선의 수
경로(Path) : 정점 Vi 에서 Vj 까지 간선으로 연결된 정점을 순서대로 나열한 리스트
경로 길이(Path Length) : 경로를 구성하는 간선의 수
사이클(Cycle) : 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로
종류
1. 방향 그래프(Directed Graph) : 간선이 방향을 가리키는 그래프
2. 무방향 그래프(Undirected Graph) : 두 정점을 연결하는 간선에 방향이 없는 그래프
3. 가중 그래프(Weighted Graph) : 간선에 가중치가 할당된 그래프
4. 순환 그래프(Cyclic Graph) : 순환 경로가 존재하는 그래프
5. 비순환 그래프(Acyclic Graph) : 순환 경로가 없는 그래프
6. 연결 그래프(Connected Graph) : 모든 노드가 서로 연결된 그래프
7. 비연결 그래프(Disconnected Graph) : 일부 노드가 연결되지 않은 그래프
8. 이분 그래프(Bipartite Graph) : 노드를 두 개의 독립적인 집합으로 나눌 수 있는 그래프

해시(Hash) & 해시 테이블(Hash Table)
(해시는 데이터를 특정 값으로 매핑하는 알고리즘 또는 데이터 매핑 방법)

효율적인 검색과 삽입 연산을 위해 설계된 자료구조
키-값 쌍의 데이터를 저장하는데 사용되고, 각 키는 해시 함수를 통해 고유 인덱스로 변환되어 배열 내에 저장됨
데이터를 저장할 버킷(Bucket) 또는 슬롯(Slot)으로 구성
해싱(Hashing) : 해시 함수를 통해 데이터를 특정 값으로 매핑하는 과정
해시함수(Hash Function)
- 임의의 데이터를 고정된 길이의 값으로 리턴해주는 함수
해시충돌(collision)과 해결방법 : 두 개 이상의 데이터가 같은 해시 값을 가지는 상황
- 체이닝(Chaining) : 충돌이 발생한 데이터를 연결 리스트로 저장
- 오픈 어드레싱(Open Addressing) : 충돌시 빈 슬롯을 찾아 데이터를 저장

집합(Set)

중복을 허용하지 않는 데이터 구조로 Array 나 List 처럼 순열 자료구조(collection)이지만 set은 비순차적으로 순서의 개념이 존재하지 않음.
특징
- 순서가 없기에 삽입 순서대로 저장되지 않음
- 수정 가능(mutable)
- 동일 값 여러번 삽입 불가능. 동일 값 여러번 삽입 시 하나의 값만 저장

시간복잡도와 공간복잡도

복잡도(complexity)
알고리즘의 성능, 효율성을 나타내는 척도
각 알고리즘이 주어진 특정 크기의 입력(n) 을 기준으로 수행시간(연산) 혹은 사용공간이 얼마나 되는지 객관적으로 비교할 수 있는 기준을 제시
```
* 점근적 표기법 3가지
1. 최상의 경우 : 오메가 표기법(Big-Ω)
2. 평균의 경우 : 세타 표기법(Big-θ)
3. 최악의 경우 : 빅오 표기법(Big-O)
주로 최악의 경우인 빅오 표기법으로 복잡도를 표기
```

시간복잡도(Time complexity)
입력값 크기(input size) 에 따라 실행되는데 걸리는 시간의 증가율을 나타내는 척도. 알고리즘의 효율성을 평가하는 중요 개념
수행시간은 실행환경에 따라 다르게 측정되기 때문에 기본 연산의 실행 횟수로 수행 시간을 평가함.

빅오 표기법
- O(1)상수시간 : 입력 크기에 상관없이 일정한 시간이 걸리는 알고리즘. ex) 배열의 특정 인덱스 접근
- O(log n)로그시간 : 입력 크기가 커질수록 처리시간이 log(지수 함수의 역함수)만큼 짧아지는 알고리즘 ex) 이진탐색(Binary Search)
- O(n)선형시간 : 입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘 ex) 배열의 순차 검색(Linear Search)
- O(n log n)로그선형시간 : 데이터가 많아질수록 처리시간이 log 배 만큼 더 늘어나는 알고리즘 ex)병합 정렬(Merge Sort), 퀵 정렬(Quick Sort)
- O(n²)이차시간 : 데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘 ex)버블 정렬(Bubble Sort), 삽입 정렬
- O(2^n)지수시간 : 데이터가 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘. 재귀가 역기능을 할 경우도 해당 ex) 피보나치 수열(재귀 구현)

O(1) < O(log n) < O(nlog n) < O(n²) < O(2ⁿ)
좌에서 우 순서로 갈수록 효율성이 떨어짐

공간복잡도
알고리즘이 실행되는 동안 사용하는 메모리의 양을 측정하는 척도

구성요소

고정 공간(Fixed Part)
- 알고리즘의 입력 크기와 상관없이 항상 일정하게 사용하는 공간
- ex) 상수, 변수, 프로그램 실행에 필요한 기본 메모리 등
- 크기 : 상수 O(1)
가변 공간(Variable Part)
- 입력 크기(n) 에 따라 증가하거나 감소하는 공간
- ex) 배열, 리스트, 동적 데이터 구조
- 크기 : O(n), O(n²) 등
재귀 또는 호출 스택 공간(Recursion/Function Call Stack Space)
- 재귀함수 호출시 사용하는 메모리
- 재귀 깊이에 따라 메모리 사용량 달라짐
- 크기 : 함수 호출 횟수 X 호출당 메모리 사용량

공간복잡도 최적화
- 중복 데이터 줄이기 위해 메모리를 공유하고, 재귀 대신 반복을 사용. 효율적인 데이터 구조 선택 등으로 최적화

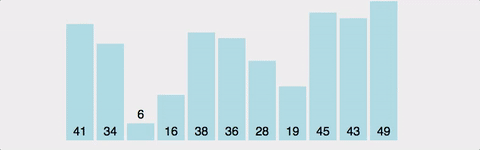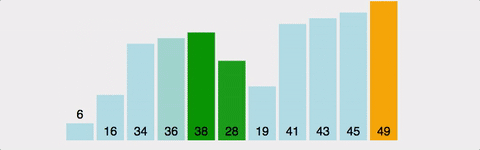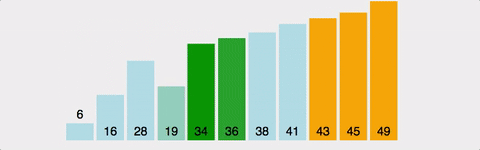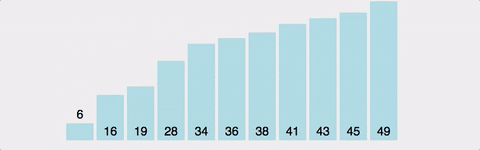
거품정렬(Bubble Sort)

서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정렬하는 알고리즘

거품 정렬은 선택 정렬과 유사한 알고리즘.

정렬 방법

1회전에 첫 번째 원소와 두 번째 원소를, 두 번째 원소와 세 번째 원소를... 이런 식으로 마지막 -1 번째 원소와 마지막 원소를 비교하며 조건에 맞지 않는다면 서로 교환.
1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 원소까지는 정렬에서 제외됨. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어남.

Java Code

void bubbleSort(int[] arr) {
    int temp = 0;
	for(int i = 0; i < arr.length; i++) {       // 1.
		for(int j= 1 ; j < arr.length-i; j++) { // 2.
			if(arr[j-1] > arr[j]) {             // 3.
                // swap(arr[j-1], arr[j])
				temp = arr[j-1];
				arr[j-1] = arr[j];
				arr[j] = temp;
			}
		}
	}
}

i는 제외될 원소의 갯수를 의미한다. 1회전이 끝난 후 배열의 마지막 위치에는 가장 큰 원소가 위치하기 때문에 하나씩 증가시켜준다.
원소를 비교할 index를 뽑는 반복문으로 j는 현재 원소를 가리키고, j-1은 이전 원소를 가리키게 되므로, j는 1부터 시작한다.
현재 가리키고 있는 두 원소의 대소를 비교한다, 해당 코드는 오름차순 정렬이므로 현재 원소보다 이전 원소가 더 크다면 이전 원소가 뒤로 가야하므로 서로 자리를 교환해준다.

시간복잡도

(n-1) + (n-2) + (n-3) + ..... + 2 + 1 => n(n-1) / 2
이므로 O(n^2)이다

Bubble Sort는 정렬이 돼있던 안돼있던, 2개의 원소를 비교하기 때문에 최선, 평균, 푀악의 경우 모두 시간 복잡도가 동일하다.

공간복잡도
주어진 배열 안에서 교환(swap)을 통해 정렬이 수행되므로 O(n)이다.

장점

구현이 간단하고, 소스코드가 직관적
정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
안전 정렬(stable Sort)이다.

단점

시간복잡도가 최악, 최선, 평균 모두 O(n^2)으로, 굉장히 비효율적이다.
정렬 돼있지 않은 원소가 정렬 됐을때의 자리로 가기 위해서, 교환 연산(swap)이 많이 일어나게 된다.

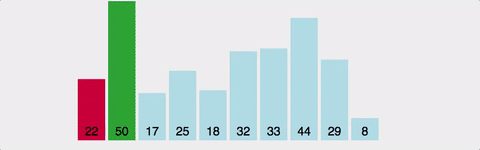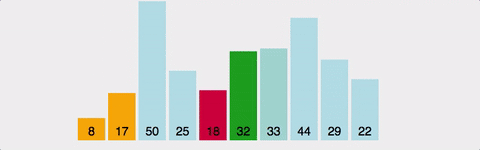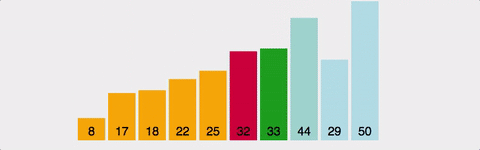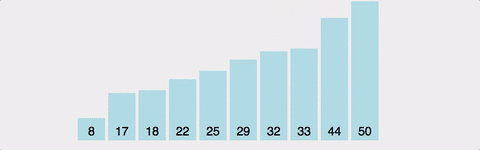
선택 정렬(Selection Sort)

해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘

선택 정렬은 거품 정렬과 유사한 알고리즘.

정렬방법
1. 주어진 배열 중에 최소값을 찾는다.
2. 그 값을 맨 앞에 위치한 값과 교체한다.(pass)
3. 맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다.

Java Code

void selectionSort(int[] arr) {
    int indexMin, temp;
    for (int i = 0; i < arr.length-1; i++) {        // 1.
        indexMin = i;
        for (int j = i + 1; j < arr.length; j++) {  // 2.
            if (arr[j] < arr[indexMin]) {           // 3.
                indexMin = j;
            }
        }
        // 4. swap(arr[indexMin], arr[i])
        temp = arr[indexMin];
        arr[indexMin] = arr[i];
        arr[i] = temp;
  }
}

위치(index)를 선택해준다.
i + 1 번째 원소부터 선택한 위치(index)의 값과 비교를 시작한다.
오름차순이므로 현재 선택한 자리에 있는 값보다 순회하고 있는 값이 작다면, 위치(index)를 갱신해준다.
'2'번 반복문이 끝난 뒤에는 indexMin에 '1'번에서 선택한 위치(index)에 들어가야하는 값의 위치(index)를 갖고 있으므로 서로 교환(swap)해준다.

시간복잡도

데이터의 개수가 n개라고 했을 때,

첫 번째 회전에서의 비교횟수 = 1 ~ (n-1) => n-1
두 번째 회전에서의 비교횟수 : 2 ~ (n-1) => n-2
...

(n-1) + (n+2) + .... + 2 + 1 => n(n-1) / 2

비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 배열을 정렬하는데 O(n^2) 만큼의 시간이 걸린다. 최선, 평균, 최악의 경우 시간복잡도는 O(n^2) 으로 동일하다.

공간복잡도

주어진 배열 안에서 교환(swap)을 통해 정렬이 수행되므로 O(n) 이다.

장점

Bubble Sort와 마찬가지로 알고리즘이 단순하다.
정렬을 위한 비교 횟수는 많지만, Bubble Sort에 비해 실제로 교환하는 횟수는 적기 때문에 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적이다.
Bubble Sort와 마찬가지로 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)

단점

시간복잡도가 O(n^2)으로 비효율적이다.
불안정 정렬(Unstable Sort)이다.

병합정렬

주어진 배열을 작은 단위로 나누고, 정렬된 부분 배열들을 병합해서 최종적으로 정렬하는 방식

작동원리
1. 분할(Divide)
- 배열을 반으로 나누어 재귀적으로 작게 분할
- 분할을 계속해서 배열이 길이 1이 될 때까지 반복
2. 정복(Conquer)
- 길이 1인 배열은 이미 정렬된 상태이므로, 두 배열을 병합하여 정렬
3. 병합(Merge)
- 두 개의 정렬된 배열을 합쳐 하나의 정렬된 배열로 만듦

시간복잡도

분할단계 : 배열의 크기를 계속 반으로 나눔 -> O(log n)
병합단계 : 각 단계에서 모든 요소를 병합 -> O(n)

병합정렬의 시간복잡도는 O(n log n)

n 개의 요소가 있을때 n 이 2의 k 제곱이라면 밑이 2인 로그를 취했을때, k만큼 반복해야 크기가 1인 배열로 분할 가능
그리고 다시 합칠때 각 요소들을 비교해서 정렬하며 병합하기 때문에 비교연산도 시간복잡도에 포함

퀵정렬

분할정복(Divide adn Conquer) 알고리즘의 종류로 배열의 한 요소를 기준(pivot)으로 삼아 작은 값과 큰 값을 나누어 정렬하는 방식
추가 메모리가 거의 필요하지 않음(제자리정렬)

작동원리
1. 분할(Divide)
- 배열에서 하나의 요소를 기준(pivot)으로 선택
- 기준보다 작은 요소는 왼쪽, 큰 요소는 오른쪽에 위치
2. 정복(Conquer)
- 왼쪽과 오른쪽 부분에 대해 재귀적으로 퀵 정렬 수행
3. 결합(Combine)
- 재귀적으로 정렬된 부분 배열들을 합침(이때 병합 과정은 없음)

시간복잡도
이미 정렬된 배열에서 첫 요소를 피벗으로 선택했을 때 -> O(n²)

김석재

이전 포스트

[CS]자료형

초심으로 돌아가서 자료형을 공부하면서 연관되는 개념까지 싸그리 학습해보자

자료형

자료형의 분류

컴퓨터 메모리

자료구조

시간복잡도와 공간복잡도

자바스크립트에서 문자열을 감쌀 때 무엇을 사용하면 좋을까? & JSON 이란?

0개의 댓글